字符串匹配算法
字符串匹配一直是一个热门的算法。本文主要讲两种,普通方法(回溯)+高级方法(KMP)。
一、回溯法求子串位置(普通方法)
算法思想:
给定两个指针:i、j,分别指向主串的第pos个位置和子串的第一个位置。比较两个指针所指的字符:如果相等,则继续比较后续字符;若不等,则 i 指针跑到pos的下一个位置上,j 指针继续从第1个位置开始比较……直到找到对应的子串。
我们发现每次失配时,指针 i 都会重新回到之前位置的下一个位置上,这边是“回溯”的体现。
给定两个指针:i、j,分别指向主串的第pos个位置和子串的第一个位置。比较两个指针所指的字符:如果相等,则继续比较后续字符;若不等,则 i 指针跑到pos的下一个位置上,j 指针继续从第1个位置开始比较……直到找到对应的子串。
我们发现每次失配时,指针 i 都会重新回到之前位置的下一个位置上(有点绕,多想想),这边是“回溯”的体现。
int Index(SString *S, SString *T, int pos) {
int i = pos; int j = 1;
while(S[i] != '\0' && T[j] != '\0') { //只要有一个串走完了,那么就退出循环
if(S[i] == T[j]) { //如果相等,则继续比较后续字符
i++; j++;
}else {
i = i-j+2; //i指针跑到隔壁位置上————回溯法的体现
j = 1; //重置j指针
}
}
if(T[j] == '\0') return i-j; //返回子串在主串的第一个匹配字符的位置
else return 0; //不匹配,返回0
}
算法分析:
若设n和m分别是主串和子串的长度,则一般情况下,该算法的时间复杂度为O(n + m)。但是在最坏情况下,它的复杂度为O(n * m)【主串和子串的前面字符都匹配,只有最后一个字符不一样】于是我们想找一种更好、更稳定的算法
二、KMP算法(非回溯法)
对第一种方法的改进
在第一种方法下,我们每次失配都要重新把 i 指针放到其隔壁的位置上,而经过实践,我们发现有时候这样做不高效,如果能直接移动模式串就好了。
于是我们提出了改进方法:在新的算法模式下,我们不需要对 i 指针进行回溯,我们只用向右移动模式串就行了。
但是这样我们需要解决一个问题:模式串要移动多远,即主串中第 i 个字符应与模式的第几个字符比较?
算法思想:
假设主串为“s1, s2, s3 …… sn”,模式串为“p1, p2, p3 …… pm”
1.若设失配后主串第 i 项应该与模式中第 k 个字符继续比较,则模式中前 k-1 个字符的子串必须满足以下公式——“p1, p2, p3 …… pk-1” == “si-k+1, si-k+2, si-k+3 …… si-1”
2.而已经得到“部分匹配”(j 指针前的所有字符均和主串对应字符匹配)的结果是——“pj-k+1, pj-k+2, pj-k+3 …… pj-1” == “si-k+1, si-k+2, si-k+3 …… si-1”
3.由以上两式,可推得下面的式子——“p1, p2, p3 …… pk-1” == “pj-k+1, pj-k+2, pj-k+3 …… pj-1”
4.由此——当匹配过程中主串第 i 个字符和模式第 j 个字符不匹配时,只需把模式移动至它的第 k 项和主串第 i 个字符对齐就行了!
next[ ]函数的构造
既然模式的每一项都有不匹配的可能,那么我们用一个数组next[ ],来写出每一项不匹配的时候所对应的 k 值**(next[ j ] = k)**。
那么如何求出每一项的k值呢?规则如下图——

由上图可知,next[ ]函数值仅取决于模式串本身,而与其相匹配的主串无关
因此,我们求每一项next值的方法如下——
1.规定:next[1] = 0;
设:next[j+1] = k;
2.比较第 k 和第 j 个字符是否匹配——
2.1. 如果匹配(T[ k ] == T[ j ]),则next[ j + 1 ] = next[ j ] + 1;
2.2. 如果不匹配(T[ k ] != T[ j ])再看k的next[ k ]
2.2.1. 若next[ k ] == T[ j ],则next[ j + 1 ] = next[ k ] + 1;
2.2.2. 若next[ k ] != T[ j ],那么继续找next[ k ]这一项的 k 值,再比较和第 j 个字符是否匹配,如果不匹配就一直找下去……
3.最后,如果你幸运找到了匹配项,则next[ j + 1 ]就是你找到的那一项的项数 + 1
如果不幸一直没找到,那么next[ j + 1 ]就等于1。
我们来看一下获取next( )函数的代码——
//获取next[]数组的函数
void get_next(SString T, int next[]) {
int i = 1; //用于遍历模式串
next[1] = 0; //规定
int j = 0; //next数组里面的数
while(i < T(0)) {
if(j == 0 || T[i] = T[j]) { //一旦第k项和第j项匹配,那么next数组的j+1项的值就是你找到的那一项的项数 + 1
i++; j++;
next[i] = j;
}else {
j = next[j]; //如果不匹配,就找第j项对应的k值
}
}
}
现在,我们就有了模式串每一项所对应的k值了!
例如,对于模式串“a b a a b c a c”,我们可以得到如下的next函数值:
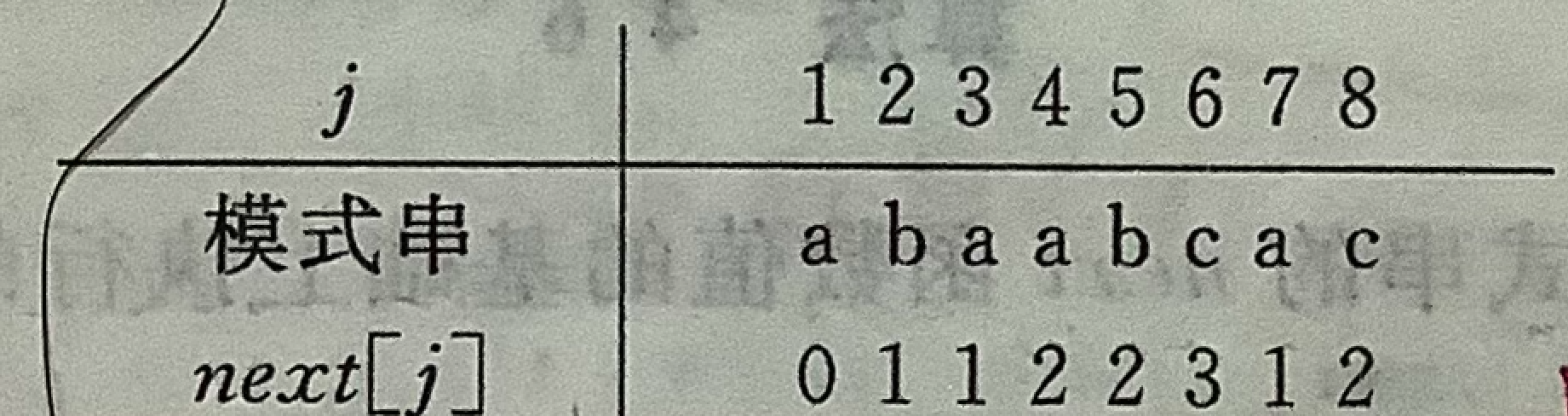
匹配步骤:
在求得模式的next[ ]函数之后,匹配可如下进行:
假设以制造 i 和 j 分别指示主串和模式中正待比较的字符,令 i 的初值为 pos, j 的初值为1(模式的第一个字符)——
- 若在匹配过程中,si = pj,则 i 和 j 分别增加1;
- 否则(si = pj),i 不变,j 退到 next[ j ] 的位置上再比较:若相等,则 i 和 j 分别增加1;不等则继续比较下一个 next 值的位置……以此类推
- 这样一直进行下去,直到出现两种情况——
- j 退到某个 next 值时字符比较相等,则两指针各自增1,继续比较下去
- j 退到其值为0(即模式串的第一个字符就失配),则此时需要把整个模式串向右滑动一位,即从主串的 s+1 位置起和模式重新进行匹配
最后,就是KMP的代码实现,实际上它和回溯法的代码差不多。
int Index(SString S, SString T, int pos) {
int i = pos; int j = 1;
while(i <= S[0] && j <= T[0]) {
if(next[j] == 0 || S[i] == T[j]) { //匹配,则比较下一个字符;要么就是模式串的第一个字符就失配,直接从主串的 s+1 位置起和模式重新进行匹配
i++; j++;
}else {
j = next[j]; //不匹配,移动模式串到下一个k处,再比较是否匹配
}
}
if(j >= T(0)) return i-T(0); //返回子串在主串的第一个匹配字符的位置
else return 0; //不匹配,返回0
}


