[DSP with spinalHDL] 00 数的表示与位数变化

在FPGA中可以自定义数位宽，这带来了极大的灵活性（相较于C语言等其他语言），但是同时带来的问题就是如何解读这些数据，以及如何处理好他们的进位关系。（之前的某个项目中，就是因为计算位数错误，导致项目结果的错误，debug很久）因此写下这篇blog，对这部分作出一定的总结。

数的表示

目前我常用的是unsigned int，signed int 以及 fixed-point三种。下面分别介绍。

Unsigned int

这种是最最简单的表示方法。

一列数:

\(a_n a_{n-1}... a_2 a_1a_0\)

他的大小等于

\(D=\sum_{i=0}^{n} a_i 2^i\)

如： b11100111

其大小等于 
\(2^7+2^6+2^5+2^2+2^1+2^0=231\)

Signed int

非常常见的有符号整数的表示方法，通常的ADC的输出就是这种形式。通常是用补码表示。

最高位为符号位，剩下的部分表示数字

定义是这样的：

• 正数的补码等于原码
• 负数的补码=负数的反码+1
• 负数的反码=符号位为1，剩下的部分为正数的取反

如果晕了就看下面的例子

比方说-3用8位Signed int表示为

# 3的Signed int
0000_0011
# 3的反码
1111_1100
# 3的补码
1111_1101   # 为0xfd

验证一下：

module invert(
	output signed [7:0] out，
	output signed [7:0] out1，
	);
    assign out = -3;
    assign out1 = 3;

    `probe(out);   // 这个是iverilog用于实现波形的语法
    `probe(out1); 
endmodule

结果为：

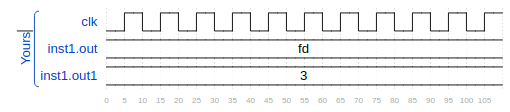
Fixed point

定点数顾名思义就是小数点的位置在二进制数中是固定的，通常需要自己定义。

如总位宽8位的，3位小数，1位符号位表示为，其中\(\Delta\)表示小数点

\(S_4 a_3 a_2 a_1 a_0 \Delta a_{-1} a_{-2} a_{-3}\)

原码的话，计算方式同Unsigned int

\(D=(-1)^{S_4}\sum_{i=-3}^{3} a_i 2^i\)

反码、补码都同Signed int，注意补码在最低位+1

举例： -1.75 Fixed point 总位宽8位的，3位小数，1位符号位表示为

# 原码
1 0001.110
# 反码
1 1110.001
# 补码
1 1110.010  # 0xf2

验证：verilog本身不支持Fixed point，这里采用更加高级的SpinalHDL来验证，具体关于SpinalHDL的可以自己看看

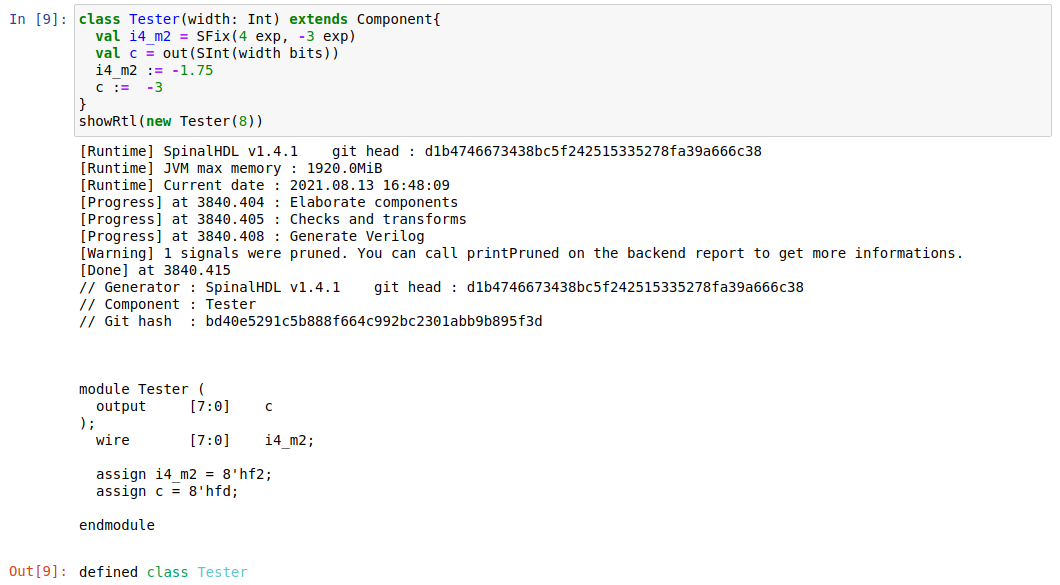
数的表示，特别是负数的表示，采用补码的形式，这种方式更容易计算加减法，而采用原码的表示，更容易计算乘法。

计算时位数的变化

在运算的时候 位宽是会变化的，因此需要注意变化的规律

加减

在两个位宽为B的加减运算中，要保证数据不溢出，结果的位宽应为B+1

在SpinalHDL中，采用 +^ 或 -^ 来保证自动推断位宽

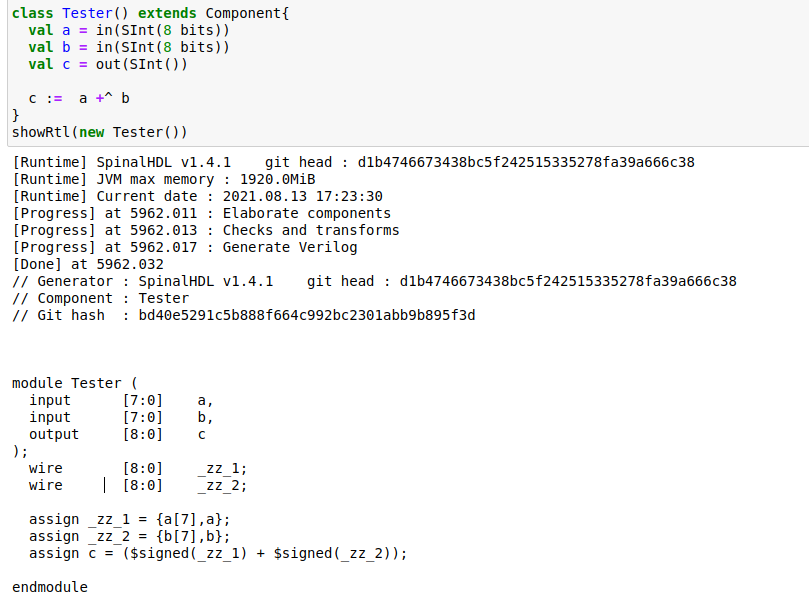
乘

乘法结果的位宽等于被乘数两个位宽之和

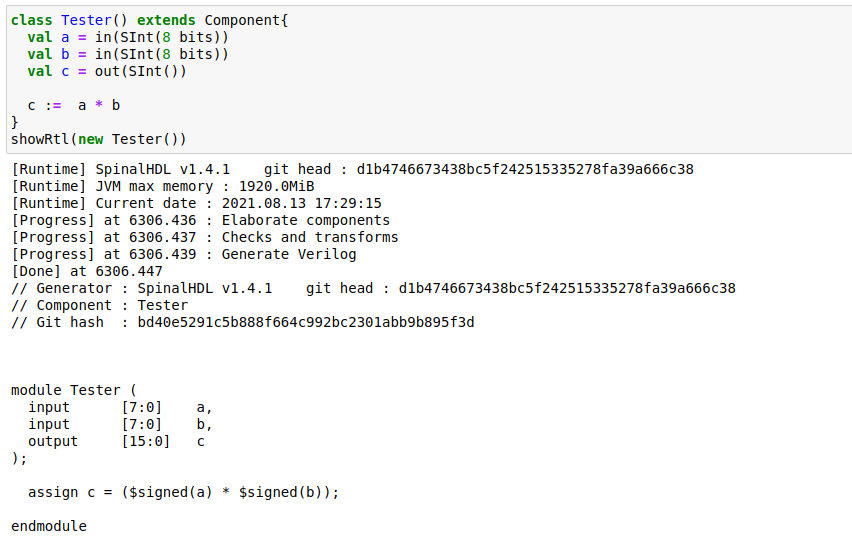
除

除法尽量使用IP核实现