函数与宏定义实验报告
实验项目:
(1)6.4.2.1编写由三角形三边求面积的函数
- 调用area()函数求三角形的面积
- 在求面积函数中运用海伦公式
(2)6.4.1.2编写求N的阶层
- 定义符号常量
- 使用长整型变量存放累乘积
- 在函数中,使用局部静态变量存放累乘积
- 使用全局变量存放累乘积
(3)6.4.1.3求两个整数的最大公约数
- 调用gcd()函数求两个整数的最大公约数
- 掌握辗转相除法求两个整数的最大公约数
(4)6.4.1.4打印输出的指定图形
- 调用trangle()函数输出三角形
- 在trangle()函数中用for循环的嵌套输出指定的结果
(5)6.4.2.1模块化程序设计
- 掌握C语言中定义函数的方法
- 掌握通过值传递调用函数的方法
二、实验内容
实验练习1:6.4.1.1 编写由三角形三边求面积的函数
- 问题的简单描述:
编写程序,从键盘输入三角形的3条边,调用三角形函数求出其面积,并输出结果。
实验代码:
#include<stdio.h> #include<math.h> float area(float a,float b,float c) { float s,p,area; s=(a+b+b)/2; p=s*(s-a)*(s-b)*(s-c); area=sqrt(p); return(area); } main(){ float x,y,z,ts; printf("请输入x,y,z:\n"); scanf("%f",&ts); ts=area(x,y,z); if (((x>0)&&(y>0)&&(z>0))&&((x+y)>z)||((x+z)>y)||((z+y)>x)) printf("area=%f\n",ts); else printf("data error!"); }

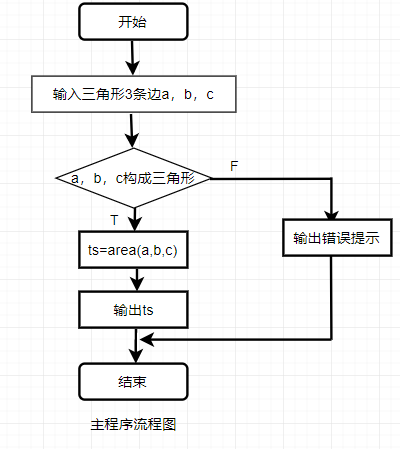
问题分析:if()的条件很简单,但实现起来其所对应的正确格式确总是出问题。可能对它的语法还是不是很了解吧。
运行结果:
实验练习2:6.4.1.2编写求N的阶层
- 问题的简单描述:
编写函数,求出从主调函数传来的数值i的阶乘值,然后将其传出主调函数并输出。 - 实验代码:
#include<stdio.h> int N=5; long function(int i) { static int f=1; f=f*i; return f; } main() { long product; int i; for(i=1;i<=N;i++) { product=function(i); printf("%d\n",product); } }
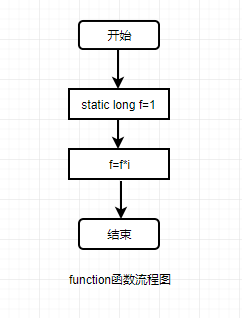
- 流程图:
![]()
![]() 问题分析:其实主要还是对阶层函数代码实现的一个要求,main()函数对它的一定范围的实现,加上用for()循环进行约束。在搞清楚阶层函数的思路后就比较好处理了。
问题分析:其实主要还是对阶层函数代码实现的一个要求,main()函数对它的一定范围的实现,加上用for()循环进行约束。在搞清楚阶层函数的思路后就比较好处理了。
运行结果:![]()
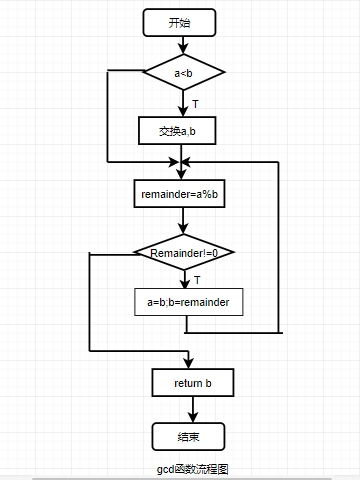
实验练习3:6.4.1.3求两个整数的最大公约数
- 问题的简单描述:
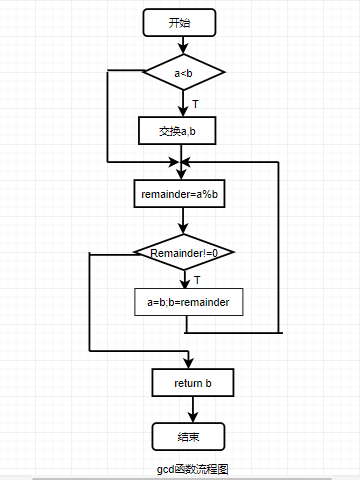
编写程序,从键盘输入两个整数,调用gcd()函数求它们的最大公约数,并输出结果。 - 实验代码:
#include<stdio.h> int gcd(int a,int b) { int c; int remainder; if(a<b) { c=a; a=b; b=c; } remainder=a%b; while(remainder!=0) { a=b; b=remainder; remainder=a%b; } return b; } main() { int x,y; int fac; printf("请输入两个整数x,y:\n"); scanf("%d%d",&x,&y); fac=gcd(x,y); printf("The great common divisor is :%d\n",fac); }
![]()
![]()
问题分析:有两个地方我觉得是关键所在。第一个是,引入一个值“c”实现a与b的互换。还有就是在while循环中为什么要加入‘remainder=a%b’。因为在第一个‘remainder1=a%b’结束之后,我们将要进行下一步‘remainder2=b%reminder1’,也就是为了循环计算“‘remainder=a%b’”,我们令a=b;b=remainder.但是该循环是在while中进行的,并不会经过第一个‘‘remainder=a%b’’,所以需要在while()循环中再加一个‘remainder=a%b’。
运行结果:
![]()
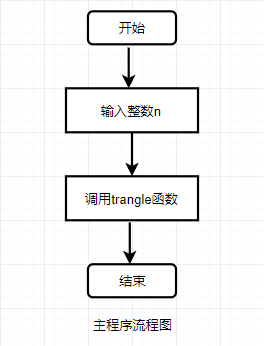
实验练习4:6.4.1.4打印输出的指定图形
- 问题的简单描述:
输入整数n,输出高度为n的等边三角形。 - 实验代码:
#include<stdio.h> void trangle(int n) { int i,j; for(i=0;i<n;i++) { for(j=i;j<=n-2;j++) printf(" "); for(j=0;j<=2*i;j++) printf("*"); printf("\n"); } } main() { int n; printf("亲输入一个整数n:\n"); scanf("%d",&n); printf("\n"); trangle(n); }
- 流程图:
![]()
![]()
问题分析:几何图形的代码实现思路一般是将其分为几个部分,用过for()循环分别进行完成。当然对于for()中的循环体语句有不同的表达,其中一般为前者为变量,则其约束条件为常量;前者为常量,则约束条件为变量。另外,“<=”比“<”范围多一,当自变量取“1”/“0”时约束范围又有所改变,不过都不是很大的问题。
- 运行结果:
![]()
实验练习5:6.4.2.1模块化程序设计
- 问题的简单描述:
若正整数A的所有因子(包括1但不包括自身,下同)之和为B,而B的因子之和为A,则称A和B为一对亲密数。例如,6的因子之和为1+2+3=6,因此6与6为一对亲密数(即6自身构成一对亲密数);又如,220的因子之和为1+2+4+5+10+11+20+22+44+55+110=284,而284的因子之和为1+2+4+71+142=220,因此,220与284为一对亲密数。
求500以内的所有的亲密数对。
具体要求如下:
(1)编制一个函数facsum(m),返回给定正整数m的所有因子(包括1但不包括自身)之和。
(2)编制一个主函数,调用(1)中的函数facsum(),寻找并输出500以内的所有亲密数对。
(3)输出要有文字说明。在输出每对亲密数时,要求从小到大排列并去掉重复的亲密数对。
(4)所有函数中的循环均为for循环。 - 实验代码:
#include<stdio.h> int facsum(int m) { int sum=1,f=2; while(f<=m/2) { if (m%f==0) sum=sum+f; f++; } return sum; } main() { int m=3,n,k; while(m<=500)
{n=facsum(m); k=facsum(n); if(m==k&&m<=n) printf("%d%d\n",m,n); m++; } }流程图:

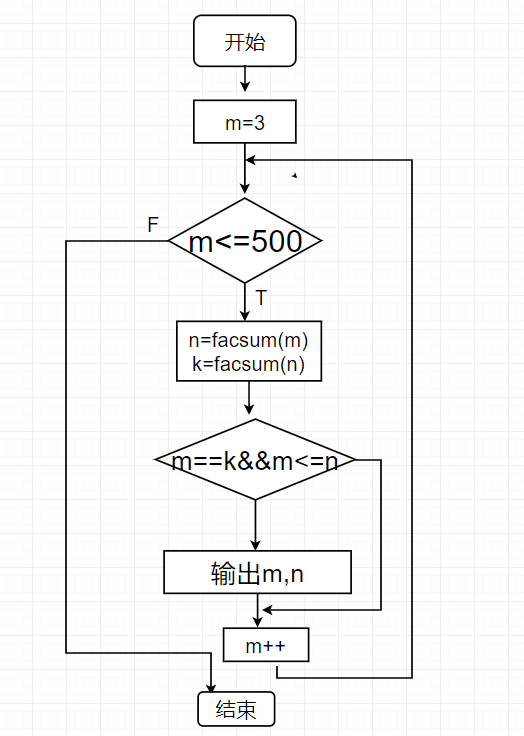
问题分析:其实首先要理解“亲密数”的概念才能够看懂流程图,但是要进一步自己构思出流程思路还需要加强训练。那么,看到程序的‘m的因子之和’的函数,其核心是通过在给定的范围不断相余,再通过“return”返回到下一个循环进行累加的一个过程。
main()函数里关键还是其判断条件以及要输出的是哪两个数。由其概念我们知道,输出的是facsum()函数的输入值m以及该函数的的输出值n.k值起到的是一个检验效果,所以在if()条件里要判断是否m==k。但其实,我个人对为什么要同时m<=n,表示很迷,知道的宝贝们欢迎为我解惑留言![]() .
.
运行结果:

实验小结:
对着流程图慢慢来,都不是什么问题,只是操作完之后还是一脸懵逼,正在着手解决这一“世纪”难题。
其实,对一些细节要求还是要忒别注意的,不然很难发现,导致自己码下去的心情都么有了。

 问题分析:其实主要还是对阶层函数代码实现的一个要求,main()函数对它的一定范围的实现,加上用for()循环进行约束。在搞清楚阶层函数的思路后就比较好处理了。
问题分析:其实主要还是对阶层函数代码实现的一个要求,main()函数对它的一定范围的实现,加上用for()循环进行约束。在搞清楚阶层函数的思路后就比较好处理了。





 浙公网安备 33010602011771号
浙公网安备 33010602011771号