动态规划之矩阵连乘

什么是动态规划

动态规划（英语：Dynamic programming，简称 DP），是一种在数学、管理科学、计算机科学、经济学和生物信息学中使用的，通过把原问题分解为相对简单的子问题的方式求解复杂问题的方法。动态规划常常适用于有重叠子问题和最优子结构性质的问题。

 1 /* Matrix.h */
 2 
 3 #pragma once
 4 #ifndef MATRIX_H
 5 #define MATRIX_H
 6 
 7 class Matrix
 8 {
 9 public:
10     Matrix();         //构造函数
11     ~Matrix();        //析构函数
12     bool Run();       //运行接口函数
13 private:
14     int W;         //记录矩阵的个数
15     int **m;       //存放最优值，即最小运算量
16     int **s;       //断开位置
17     int *p;        //存放
18 
19     bool Input();  //处理输入
20     bool MatrixChain();//计算最优值算法
21     void Traceback(int i, int j, int **s);   //输出矩阵加括号的方式
22 };
23 
24 #endif

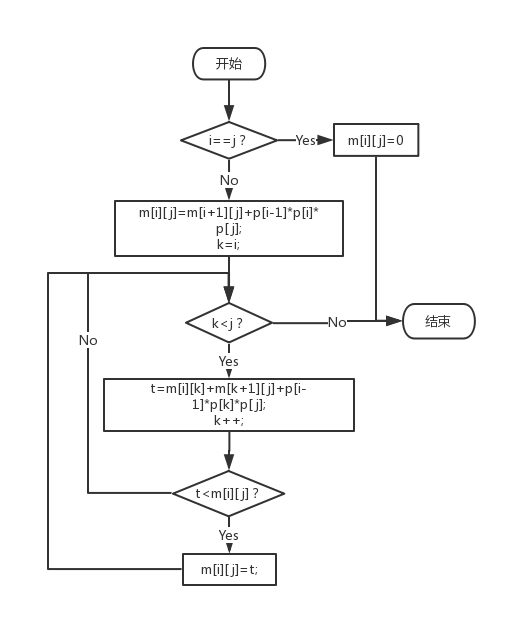
  1 /* Matrix.c */
  2 
  3 #define N 50
  4 #include <iostream>
  5 #include <stdlib.h>
  6 #include "Matrix.h"
  7 
  8 //构造函数，作变量初始化工作，为指针分配内存空间
  9 Matrix::Matrix()
 10 {
 11     W = 0;
 12     m = new int*[N];
 13     s = new int*[N];
 14     for (int i = 0; i<N; i++)
 15     {
 16         m[i] = new int[N];
 17         s[i] = new int[N];
 18     }
 19     p = new int[N];
 20 }
 21 
 22 //析构函数，释放内存
 23 Matrix::~Matrix()
 24 {
 25     for (int i = 0; i<N; i++)
 26     {
 27         delete[]m[i];
 28         delete[]s[i];
 29     }
 30     delete[]m;
 31     delete[]s;
 32     delete[]p;
 33 }
 34 
 35 //处理键盘输入
 36 bool Matrix::Input()
 37 {
 38     using namespace std;
 39     int w;
 40     cout << "矩阵个数：";
 41     cin >> w;
 42     W = w;
 43     cout << "输入矩阵A1维数" << "：";
 44     cin >> p[0] >> p[1];
 45     for (int i = 2; i <= W; i++)
 46     {
 47         int m = p[i - 1];
 48         cout << "输入矩阵A" << i << "维数：";
 49         cin >> p[i - 1] >> p[i];
 50         if (p[i - 1] != m)
 51         {
 52             cout << endl << "维数不对，矩阵不可乘！" << endl;
 53             exit(1);
 54         }
 55         //cout<<endl;
 56     }
 57     if (p != NULL)
 58         return true;
 59     else
 60         return false;
 61 }
 62 
 63 //计算最优值算法
 64 bool Matrix::MatrixChain()
 65 {
 66     if (NULL == p)
 67         return false;
 68     for (int i = 1; i <= W; i++)
 69         m[i][i] = 0;
 70     for (int r = 2; r <= W; r++)
 71         for (int i = 1; i <= W - r + 1; i++)
 72         {
 73             int j = i + r - 1;
 74             m[i][j] = m[i + 1][j] + p[i - 1] * p[i] * p[j];
 75             s[i][j] = i;
 76             for (int k = i + 1; k<j; k++)
 77             {
 78                 int t = m[i][k] + m[k + 1][j] + p[i - 1] * p[k] * p[j];
 79                 if (t<m[i][j])
 80                 {
 81                     m[i][j] = t;
 82                     s[i][j] = k;
 83                 }
 84             }
 85         }
 86     return true;
 87 }
 88 
 89 //输出矩阵结合方式，加括号
 90 void Matrix::Traceback(int i, int j, int **s)
 91 {
 92     using namespace std;
 93     if (i == j)
 94     {
 95         cout << "A" << i;
 96     }
 97     else if (i + 1 == j)
 98     {
 99         cout << "(A" << i << "A" << j << ")";
100     }
101     else
102     {
103         cout << "(";
104         Traceback(i, s[i][j], s);
105         Traceback(s[i][j] + 1, j, s);
106         cout << ")";
107     }
108 }
109 
110 bool Matrix::Run()
111 {
112     using namespace std;
113     if (Matrix::Input())
114     {
115         if (Matrix::MatrixChain())
116         {
117             Matrix::Traceback(1, W, s);
118             cout << endl;
119             return true;
120         }
121         else
122             return false;
123     }
124     else
125         return false;
126 }

 1 /* Main.c */
 2 
 3 #include "Matrix.h"
 4 
 5 int main()
 6 {
 7     Matrix matrix;
 8     matrix.Run();
 9     return 0;
10 }

posted on 2021-06-17 14:54 Arthurian 阅读(190) 评论(0) 编辑收藏举报