2023/4/11小记
多源汇最大流
建一个超级原点,一个超级汇点就行,注意数组大小。
//#pragma GCC optimize(2)
#include<bits/stdc++.h>
using namespace std;
const int N=1e6+6,M=1e6+5;
class Dinic{
public :
const int INF=2e9;
inline void add(int u,int v,int w){
AddEdge(u,v,w);
AddEdge(v,u,0);
}
int S,T;
int do_Dinic(){
int ret=0;
while(bfs()){
ret+=dfs(S,INF);
}
return ret;
}
void set_ST(int ss,int tt){S=ss,T=tt;}
private :
int hd[N],cur[N],cntedge=1;
struct node{int to,val,nxt;}a[N];
inline void AddEdge(int u,int v,int w){
a[++cntedge]=(node){v,w,hd[u]};
hd[u]=cntedge;
}
int dis[N];
bool bfs(){
memset(dis,-1,sizeof(dis));
memcpy(cur,hd,sizeof(hd));
queue<int> q;
q.push(S);dis[S]=0;
while(!q.empty()){
int u=q.front();
q.pop();
for(int i=hd[u];i;i=a[i].nxt){
int to=a[i].to;
if(dis[to]==-1&&a[i].val){
dis[to]=dis[u]+1;
q.push(to);
}
}
}
return dis[T]!=-1;
}
int dfs(int u,int flow){
if(u==T) return flow;
int now=0;
for(int i=cur[u];i&&now<flow;i=a[i].nxt){
cur[u]=i;
int to=a[i].to;
if(dis[to]==dis[u]+1&&a[i].val){
int dlt=dfs(to,min(flow-now,a[i].val));
a[i].val-=dlt,a[i^1].val+=dlt;
now+=dlt;
}
}
return now;
}
}D;
int n,m,cnts,cntt;
int main(){
scanf("%d%d",&n,&m);
scanf("%d%d",&cnts,&cntt);
D.set_ST(n+1,n+2);
for(int i=1;i<=cnts;i++){
int tmp;scanf("%d",&tmp);
D.add(D.S,tmp,D.INF);
}
for(int i=1;i<=cntt;i++){
int tmp;scanf("%d",&tmp);
D.add(tmp,D.T,D.INF);
}
for(int i=1;i<=m;i++){
int u,v,w;
scanf("%d%d%d",&u,&v,&w);
D.add(u,v,w);
}
cout<<D.do_Dinic();
return 0;
}
最大密度子图
首先二分答案;
分数规划:
\(\frac{E}{V} \ge mid\)转化成 \(E-V\times mid\ge 0\)。
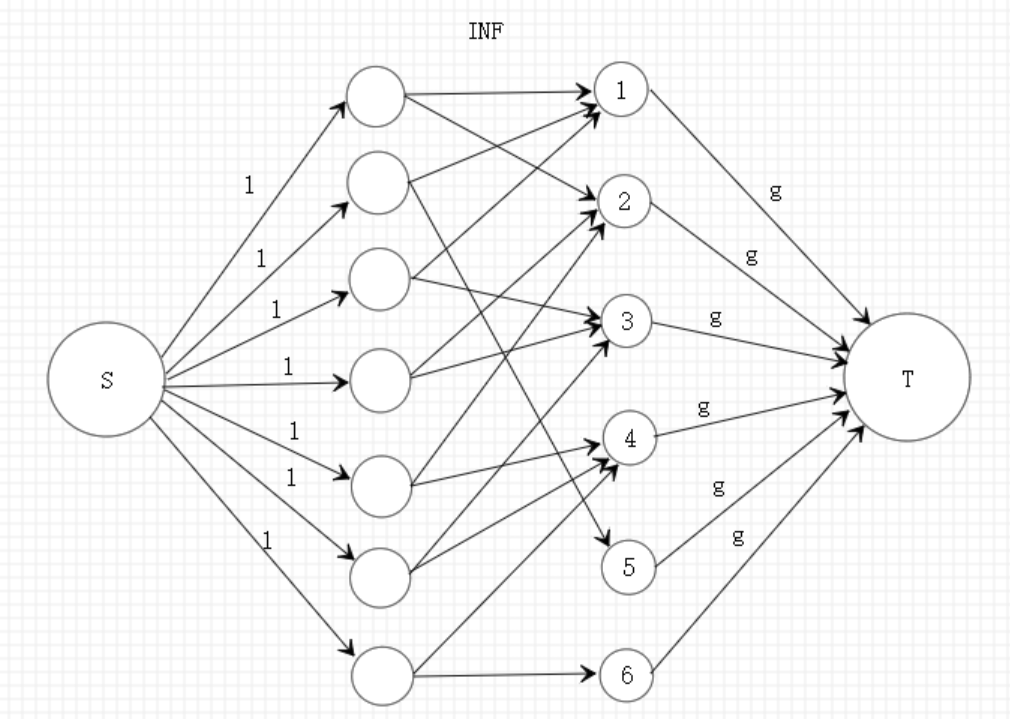
然后建图。
选一个点的花销是mid,不选这个点的代价是失去这个点出去的边。
我建的图是这个东西反过来 问题不大。输出答案好讨厌qwq。
//#pragma GCC optimize(2)
#include<bits/stdc++.h>
using namespace std;
const int N=1e4+5,M=1e5+5;
template<class T>void read(T &x){
x=0;int f=0;char ch=getchar();
while(ch<'0'||ch>'9') {f|=(ch=='-');ch=getchar();}
while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
x=f?-x:x;return;
}
#define db double
bool vis[N];
int ans;
int n,m,k;
class Dinic{
public :
const db INF=2e9;
inline void add(int u,int v,db w){
AddEdge(u,v,w);
AddEdge(v,u,0);
}
int S,T;
int do_Dinic(){
db ret=0;
while(bfs()){
ret+=dfs(S,INF);
}
return ret;
}
void set_ST(int ss,int tt){S=ss,T=tt;}
inline void init(){
memset(hd,0,sizeof(hd));
cntedge=1;
}
void findans(int u){
if(u>=1&&u<=n) ans++;
vis[u]=1;
for(int i=hd[u];i;i=a[i].nxt)
if(!vis[a[i].to]&&a[i].val>0)findans(a[i].to);
return ;
}
private :
int hd[N],cur[N],cntedge=1;
struct node{int to;db val;int nxt;}a[N];
inline void AddEdge(int u,int v,db w){
a[++cntedge]=(node){v,w,hd[u]};
hd[u]=cntedge;
}
int dis[N];
bool bfs(){
memset(dis,-1,sizeof(dis));
memcpy(cur,hd,sizeof(hd));
queue<int> q;
q.push(S);dis[S]=0;
while(!q.empty()){
int u=q.front();
q.pop();
for(int i=hd[u];i;i=a[i].nxt){
int to=a[i].to;
if(dis[to]==-1&&a[i].val){
dis[to]=dis[u]+1;
q.push(to);
}
}
}
return dis[T]!=-1;
}
db dfs(int u,db flow){
if(u==T) return flow;
db now=0;
for(int i=cur[u];i&&now<flow;i=a[i].nxt){
cur[u]=i;
int to=a[i].to;
if(dis[to]==dis[u]+1&&a[i].val){
db dlt=dfs(to,min(flow-now,a[i].val));
a[i].val-=dlt,a[i^1].val+=dlt;
now+=dlt;
}
}
return now;
}
}D;
struct NODE{int fr,to;}s[N];
bool check(db x){
D.init();
D.set_ST(n+m+1,n+m+2);
for(int i=1;i<=n;i++)D.add(D.S,i,x);
// for(int i=1;i<=n;i++)D.add(i,D.T,D.INF);
for(int i=1;i<=m;i++){
int tmp=n+i;
D.add(s[i].fr,tmp,1);
D.add(s[i].to,tmp,1);
D.add(tmp,D.T,1);
}
return m>D.do_Dinic();
}
int main(){
read(n),read(m);
for(int i=1;i<=m;i++){
read(s[i].fr),read(s[i].to);
}
db l=0,r=1e4,mid,eps=1e-8;
while(r-l>eps){
mid=(l+r)/2;
if(check(mid)) l=mid;
else r=mid;
}
// cout<<check(1)<<" "<<check(1.19)<<" "<<check(1.25)<<endl;
check(l);
// debug(l);
D.findans(D.S);
if(l==0){
printf("1\n1");return 0;
}
printf("%d\n",n-ans);
for(int i=1;i<=n;i++)
if(!vis[i]) printf("%d\n",i);
return 0;
}
[HNOI2013]切糕
不考虑D的限制的时候是好做的

考虑D的限制
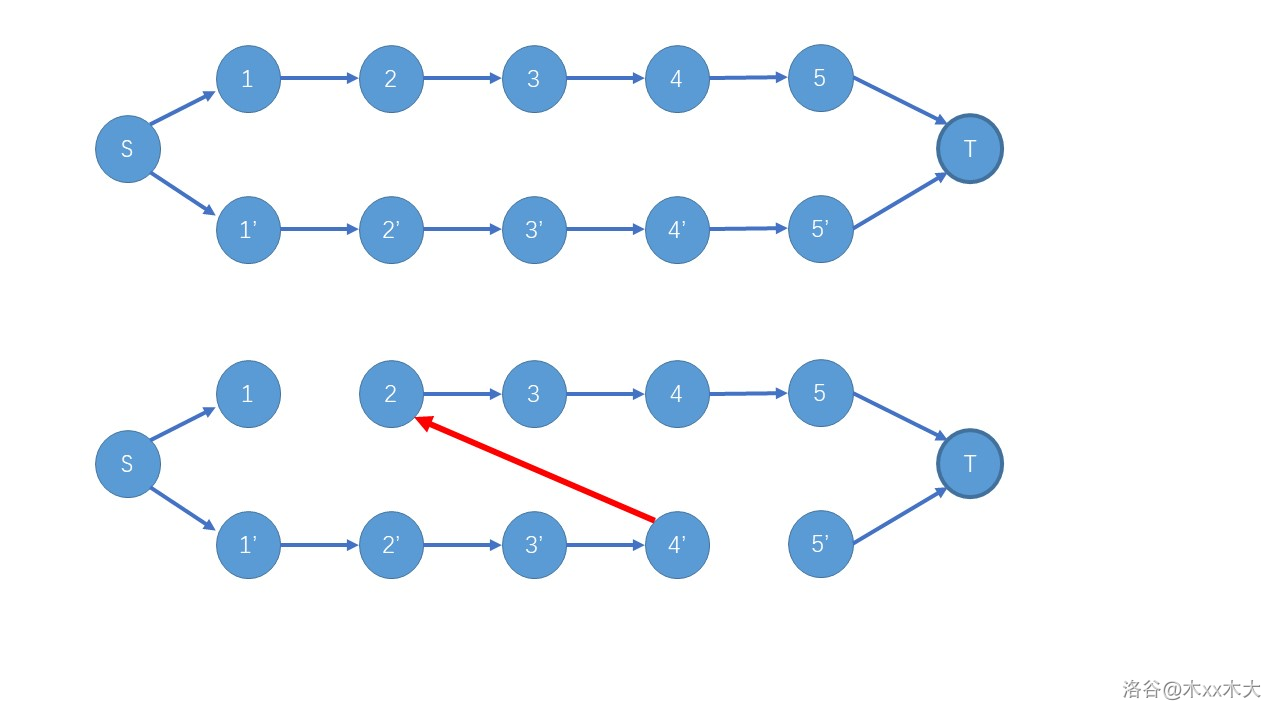
这时候如果这种选择会强迫割下一个INF,不会这么走,就行了。
dinic板子
class Dinic{
public :
const int INF=2e9;
inline void add(int u,int v,int w){
AddEdge(u,v,w);
AddEdge(v,u,0);
}
int S,T;
int do_Dinic(){
int ret=0;
while(bfs()){
ret+=dfs(S,INF);
}
return ret;
}
void set_ST(int ss,int tt){S=ss,T=tt;}
private :
int hd[N],cur[N],cntedge=1;
struct node{int to,val,nxt;}a[M<<1];
inline void AddEdge(int u,int v,int w){
a[++cntedge]=(node){v,w,hd[u]};
hd[u]=cntedge;
}
int dis[N];
bool bfs(){
memset(dis,-1,sizeof(dis));
memcpy(cur,hd,sizeof(hd));
queue<int> q;
q.push(S);dis[S]=0;
while(!q.empty()){
int u=q.front();
q.pop();
for(int i=hd[u];i;i=a[i].nxt){
int to=a[i].to;
if(dis[to]==-1&&a[i].val){
dis[to]=dis[u]+1;
q.push(to);
}
}
}
return dis[T]!=-1;
}
int dfs(int u,int flow){
if(u==T) return flow;
int now=0;
for(int i=cur[u];i&&now<flow;i=a[i].nxt){
cur[u]=i;
int to=a[i].to;
if(dis[to]==dis[u]+1&&a[i].val){
int dlt=dfs(to,min(flow-now,a[i].val));
a[i].val-=dlt,a[i^1].val+=dlt;
now+=dlt;
}
}
return now;
}
}D;
每日发癫
循着风 逆着光 告别月亮
记忆收拢 温暖过往
莫思 也莫遗忘 离别时 接过他勋章
于未来 的未来 共迎春光
莫思 也莫遗忘 用生命凝塑 的画像
永不湮灭 爱是穿越一切 的力量
(阿良良老师的莫思)

