机器学习算法 |
机器学习算法是一类从数据中自动分析获得规律,并利用规律对未知数据进行预测的算法。 |
"学习"的目的是"减熵"(减少不确定性) ※ 在信息论中,熵表示的是不确定性的量度 |
机器学习大致等同于找到一个好的函数(function)/模型(model): y=f(x) |
机器学习的"六步走": 收集数据→准备数据→选择/建立模型→训练模型→测试模型→调节参数
机器学习的"关键三步": ● 找一系列函数来实现预期的功能: 建模问题 ● 找一组合理的评价标准, 来评估函数定位好坏: 评价问题 ● 快速找到性能最佳的函数: 优化问题(例如"梯度下降"就是这个目的) |
机器学习的分类 |
无监督学习(unsupervised learning):训练样本数据和待分类的类别已知,但训练数据未加标签(label); 监督学习(supervised learning):训练样本数据和待分类的类别已知,且训练数据加了标签(label); 半监督学习(semi-supervised learning):训练样本数据和待分类的类别已知,然而训练样数据有的加了标签, 有的没加. 强化学习(reinforcement Learning): 强化学习是通过奖励或惩罚来学习怎样选择能产生最大积累奖励的行动的算法。该方法不同于监督学习技术那样通过正例、反例来告知采取何种行为,而是通过试错(trial and error)来发现最优行为策略。(联想海豚表演得好就有奖励.) |
各类机器学习的代表算法: ● 无监督学习: 例如聚类(clustering)算法和主成分分析法(principal component analysis), 聚类算法主要包括: k-means算法(属于划分式聚类方法),此外还有层次化聚类方法, 基于密度的聚类方法, 基于网格的聚类方法等.
● 监督学习: 主要包括分类(classification)算法和线性判别分析(linear discriminant analysis), 分类算法主要包括: 朴素贝叶斯算法(Naive Bayes, NB) 决策树算法(Decision Tree) 随机森林(random forest) 支持向量机算法(support vector machines, SVM) K最近邻算法(k-Nearest Neighbor,KNN) Boosting算法
● 半监督学习: 例如Semi-Supervised Support Vector Machine (S3VM)等算法
● 强化学习: 例如TD(Temporal Difference)算法、Q-learning算法、Sarsa算法等。 |
深度学习是个框架,有监督和无监督学习算法都有--CNN是监督学习; RNN既可以处理有监督学习问题,也可以处理无监督学习问题, |
※ 补充 回归分析(Regression Analysis): 确定两种或两种以上变量之间间相互依赖的定量关系 在回归分析中,如果只包括一个自变量(x)和一个因变量(y),且二者的关系可用一条直线近似地表示,这种回归分析称为一元线性回归分析。 |
人工智能 |
由机器展示的智能, 与自然智能相对. 由约翰·麦卡锡(John McCarthy)与956年提出 人工智能之父: 艾伦·图灵(Alan Turing) (Artificial intelligence (AI, also machine intelligence, MI) is intelligence displayed by machines, in contrast with the natural intelligence (NI) displayed by humans and other animals.) |
人工智能的三个时代: 运算智能, 感知智能(目前的阶段), 认知智能 |
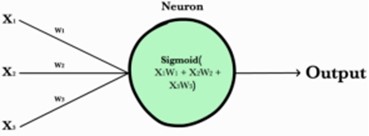
神经元(neuron) |
神经元接受多个输入(input)(x1,x2,x3...),经过 加权(weighted) 求和,并和偏置值(bias)相加, 再作用上激活函数后,得到一个输出值(input), 如果该输出值大于阈值(threshold),感知器输出1,否则输出0。 ※ 好比神经末梢感受各种外部环境的变化,最后产生电信号。 ※ 类比绩点计算, 绩点高于4.0(阈值)可以得较高的奖学金.
|
感知器(perceptron)和神经元的区别: 很多资料将两者等同, 但严格来说, 区别如下: 感知器的激活函数一般是阶跃函数(step function) 神经元的激活函一般是 sigmoid 函数或 tanh 函数等 |
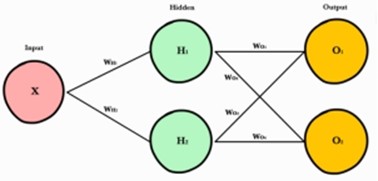
神经网络/人工神经网络,ANN=Artificial Neural Networks |
神经网络就是按照一定规则将多个神经元连接起来的网络. 一个神经网络接受多个输入, 然后将它们传入多个隐藏层的神经元, 最后输出代表了所有神经元的联合输出(combined input)的预测结果(prediction result). 神经网络包括输入层(input layer), 隐藏层(hidden), 和输出层(output layer).
|
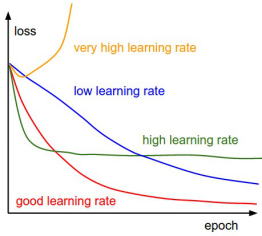
① 神经网络中的学习率(learning rate)是最重要的超参数(hyper parameter)之一, 它决定了权值等参数的更新速度, 通常取0和1之间的值。学习速率过大会导致不收敛,过小会导致收敛过慢. (收敛: converge--接近极限(to approach a limit)) ② 在梯度下降算法中, 沿着梯度的反方向方向跨多大步(magnitude)叫做学习率或步长。 ③ 权值等参数的更新发生在反向传递之后, 优化过程中(during optimization after back propagation).
Loss means error. An epoch means one iteration over all of the training data. |
※ epoch、 iteration和batchsize的区别下面按自己的理解说说这三个的区别: (1)batchsize:批大小。在深度学习中,一般采用SGD(Stochastic Gradient Descent, 随机梯度下降)训练,即每次训练在训练集中取batchsize个样本训练; (2)iteration:1个iteration等于使用batchsize个样本训练一次; (3)epoch:1个epoch等于使用训练集中的全部样本训练一次
例如: 训练集有1000个样本,batchsize=10,那么,训练完整个样本集需要:100次iteration,1次epoch。 |
※ 学习率、训练迭代次数和模型参数的初始化方式都对模型最后的准确率有一定的影响, 例如: # 设置模型 # 学习率 learning_rate = 0.01 # 训练迭代次数 training_epochs = 50 # batch大小 batch_size = 100 # 每多少次迭代显示一次损失 display_step = 1 |
超参数(hyper parameter)指的是训练之前人为设定的一些参数,它们不可以通过算法学会, 例如, K-Means算法中的簇数N, 深度学习中的"学习率"η一一与其相对的就是 可以通过算法学会的那些参数,例如权值w 和偏置b 。 |
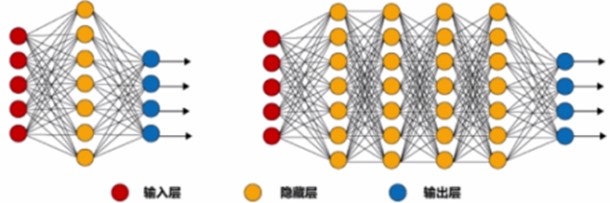
深度学习 |
多层神经网络的学习方法就是"深度学习", 由杰弗里·辛顿( Geoffrey[ˈdʒefrɪ] Hinton)于2006年提出 深度学习是个框架,有监督和无监督学习算法都有。 |
● 简单神经网络: 只有一个隐藏层 ● 深度神经网络: 大于或等于两个隐藏层 |
※ 深度学习的形象比喻: 谈恋爱 ● 第一阶段--初恋期: 相当于神经网络的输入层→设置不同的超参数 ● 第二阶段--磨合期: 相当于神经网络的隐藏层→调整参数的权重 ● 第三阶段--稳定器: 相当于神经网络的输出层→输出结果与预期比较
※ 关键是理解上面第二阶段的"调整参数权重", 例如: 经过磨合期, 男友知道他要: ● 调高"逛街"的权重(重要) ● 调高"聊天"的权重 ● 调低"玩游戏"的权重
※ 是什么算法推动了调参(tuning weight)? BP算法, 也称误差反向传播算法(Error Back-propagation Algorithm) BP算法, 具体的过程是: ① 在神经网络里正向传播参数信号, 经过隐藏层处理, 输出结果 ② 计算和预期的差距(误差), 反向传播误差, 调整网络参数权重 ③ 不断地进行: 正向传播→计算误差→反向传播→调整权重
※ 梯度下降法(Gradient Descent)是神经网络的核心方法,用于更新神经元之间的权重,以及每一层的偏置(找到最接近预定函数的权重和偏差);反向传播算法(Back-Propagation Algorithm)则是一种快速计算梯度的算法,从而能够使得梯度下降法得到有效的应用。 ※ 在隐藏层中, 不仅有调参, 还涉及到模型的调整, 例如增加神经元, 或者不让一些神经元参与计算(dropout) |
何谓神经网络训练过程中的"错"? 错(Error): 与期望的误差(Loss/Cost) |
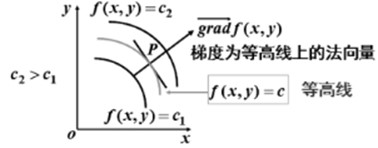
梯度下降, Gradient Descent |
函数的梯度给出了该函数最陡峭的上升方向, 梯度的反方向是该函数值局部下降最快的方向. 梯度为等高线上的法向量.
另一解释: 函数在某点的梯度是这样一个向量,它的方向与取得最大方向的导数的方向一致,而它的模为方向导数的最大值. |
梯度下降是机器学习中最核心的优化算法. 梯度下降即 沿着梯度的反方向 对模型的参数进行更新和完善,更新后的参数再次跑到隐藏层去学习,从而最小化损失函数, 一直循环直到结果收敛。 在梯度下降算法中, 沿着梯度的反方向方向跨多大步叫做学习率或步长。
※ 梯度下降中更新的参数(Parameters )指 : refer to coefficients in linear regression and weights in neural networks.
对于机器学习模型优化的问题,当我们需要求解最小值的时候,朝着梯度下降的方向走,就能找到最优值了。 |
(批量, batch)梯度下降每次用整个训练集计算梯度更新权重, 随机梯度下降(Stochastic Gradient Descent,SGD)每次用一个训练样本计算梯度更新权重, 小批量梯度下降(mini-batch)每次用部分训练样本计算梯度更新权重,比如50。 |
损失函数(loss function)或代价函数(cost function)用来度量预测错误程度. 也就是说,评价一个机器学习算法好坏时,需要提前定义一个损失函数,来判断这个算法是否是最优的,而后面不断地优化求梯度下降,使得损失函数最小,也是为了让一个算法达到意义上的最优.
交叉熵: 交叉熵(cross entropy)用来评估当前训练得到的概率分布与真实的概率分布的差异情况,减少交叉熵损失就是在提高模型的预测准确率。 |
激励函数/激活函数(activation function) 作用: 加入非线性因素,从而解决线性模型不能解决的问题。 |
常用的激励函数: sigmoid函数 Tanh函数 ReLU函数 softmax函数
※ 有开发者声称80%以上的工程都优先使用ReLU函数作为激励函数。 |
拟合(fitting) |
● under fitting: 欠拟合→样本不够或算法不精, 测试样本特性没学到 ● fitting right: 拟合完美→恰当地拟合测试数据, 泛化能力强 ● overfitting: 过拟合→"一丝不苟"地拟合测试数据, 泛化能力弱 ※ 泛化/广义化(generalize), 例如将"大雁"泛化为"鸟类" |
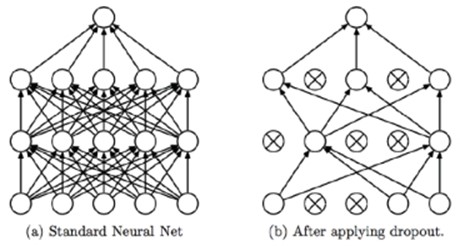
※ 解决过拟合的一些方法: ● 降低数据量 ● 正则化(regularization) ● 丢弃(dropout) |
※ L1和L2正则化(L1 and L2 Regularization) L1和L2正则化就是在代价函数后面再加上一个正则化项: ℓ1-norm和ℓ2-norm (也叫做L1范数和L2范数), 它们用于防止过拟合.
● L1正则化项是: 所有权重w的绝对值的和,乘以λ/n(这里不像L2正则化项那样,需要再乘以1/2,原因如下)
※ C0代表原始的代价函数,后面那一项就是L1正则化项
● L2正则化项是: 所有参数w的平方的和,除以训练集的样本大小n。
λ就是正则项系数,权衡正则项与C0项的比重。另外还有一个系数1/2,1/2经常会看到,主要是为了后面求导的结果方便,后面那一项求导会产生一个2,与1/2相乘刚好凑整。
※ L1正则化可以产生稀疏权值矩阵,即产生一个稀疏模型, 因此可以用于特征选择. ※ L2正则化的效果是减小w,也就是权重衰减(weight decay)→可以防止模型过拟合(overfitting);一定程度上,L1也可以防止过拟合
※ ||v||叫作范数(norm), 即向量v的长度. |
※ 使用了L1正则化项的回归称为 Lasso Regression(套索回归); 使用了L2正则化项的回归称为Ridge Regression(岭回归). |
Dropout(丢弃): 是一种超参, 用于防止过拟合, 在训练中随机的删掉节点以及他们之间所属的关系。
|
※ 特征选择(feature selection)和降维(dimensionality reduction) |
● 目的相同: 试图去减少特征数据集中的属性(或者称为特征)的数目. ● 达到目的的方法不同: ① 降维的方法主要是通过属性间的关系,如组合不同的属性得新的属性,这样就改变了原来的特征空间; ② 特征选择的方法是从原始特征数据集中选择出子集,是一种包含的关系,没有更改原始的特征空间。 |
Tensorflow |
Google开源的基于数据流图(data flow graph)的科学计算库, 适合用于深度学习等机器学习算法. Tensorflow支持CPU和GPU()搭配NVIDIA显卡两种设备,支持单机和分布式计算。 |
Tensorflow的基本概念 |
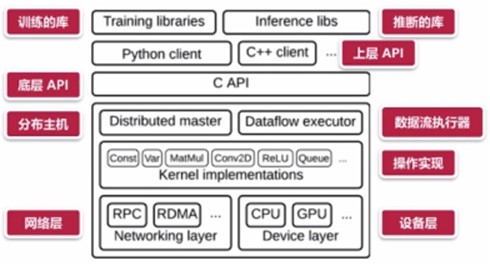
在TensorFlow中: ① 算法都被表示成计算图(computational graphs, 也叫数据流图(data flow graph)),可以把计算图看做是一种有向图, 用来表述一个计算任务. ※ Tensorflow的任务(task)与服务器(server)相关联(associate), 一个服务器由两个部分组成,第一部分是master,用于创建session,第二部分是worker,用于执行具体的计算。 ※ 为什么在运行session对象的方法的时候, 可以不用创建一个Graph对象? 因为: TensorFlow的计算都是基于图的, 如果不特殊指定,会使用系统默认图。只要定义了操作,必然会有一个图(自定义的或启动默认的)。 ----自定义图的方法:g=tf.Graph() ----查看系统当前的图:tf.get_default_graph()
② 图中的节点(node)表示操作.
③ 边: 代表不同操作(op)之间的连接,因为它们将数据从一个节点传输到另一个节点。(不同操作之间的数据流动)
④ 在边上流动的数据叫作张量(tensor), 一个张量可以看做是多维的数组或者高维的矩阵。 需要注意的是张量本身并没有保存任何值,张量仅仅提供了访问数值的一个接口,可以把它看做是数值的一种引用。 ※ Numpy的array类似Tensorflow的tensor
⑤ 在TensorFlow中,所有操作都必须在会话(session)中执行,会话负责分配和管理各种资源。 ※ Session是一个类,作用是把graph ops部署到Devices(CPUs/GPUs)上,并提供具体执行这些op的方法。 |
Tensorflow的详细架构:
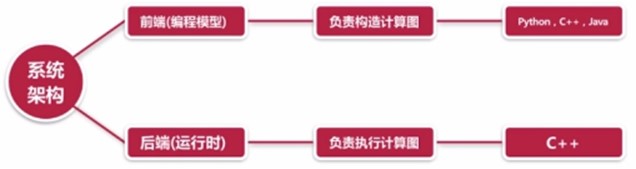
Tensorflow的基本架构:
|
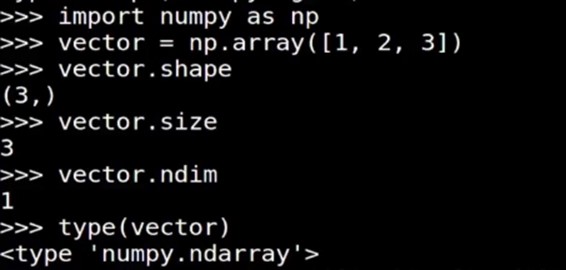
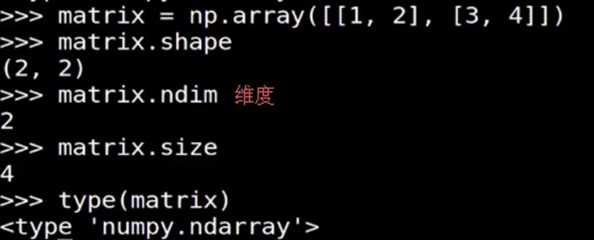
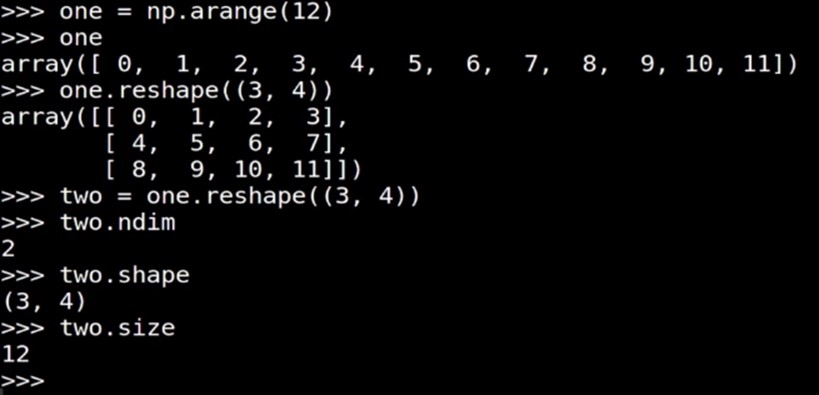
向量的shape, size, ndim, type 矩阵的shape, size, ndim, type |
一维数组->向量 二维数组->矩阵(行、列数目相同时, 叫方阵) 把矩阵 A 的行 换成同序数的列 得到的矩阵,叫做 A 的转置矩阵,记作 AT。
大部分元素是0的矩阵称为稀疏矩阵.
Tensorflow使用三个密集张量:indices,values,dense_shape,来表示一个稀疏张量。 Tensorflow represents a sparse tensor as three separate dense tensors: indices, values, and dense_shape. |
阶(dimension/rank/order): 二阶就是 2*2的矩阵 三阶就是3*3的矩阵 |
|
向量点乘(内积、点积、数量积)和叉乘(外积、向量积) |
标量 [scalar quantity]∶只有大小但没有方向概念的量(如质量或时间) 矢量/向量 [vector] 有大小和方向的物理量,如速度、动量、力.
向量的内积是一标量 向量的外积是一矢量(就是向量) |
內积:
外积:
|
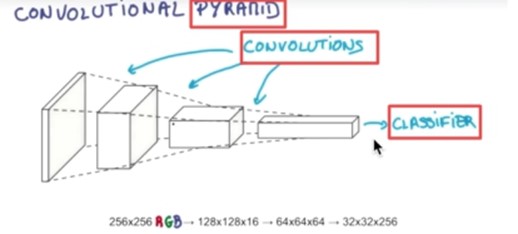
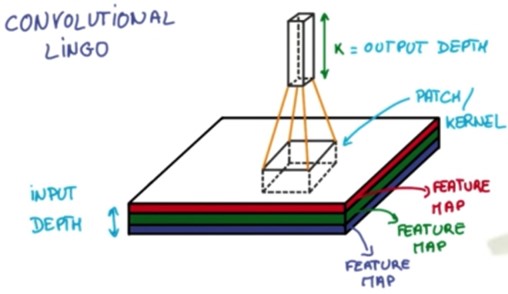
卷积神经网络, CNN(Convolutional Neural Networks) |
卷积神经网络简单讲就是把一个图片的数据传递给CNN,原涂层是由RGB组成,然后CNN把它的厚度加厚,长宽变小,每做一层都这样被拉长,最后形成一个分类器:
如果想要分成十类的话,那么就会有0到9这十个位置,这个数据属于哪一类就在哪个位置上是1,而在其它位置上为零。 在 RGB 这个层,每一次把一块核心抽出来,然后厚度加厚,长宽变小,形成分类器:
|
Recurrent Neural Networks, RNN, 循环神经网络 |
※ 处理图片分类的时候,可以把图片一张一张放入分类器中独立进行判断。但是处理语音以及文字的时候,不能把发音独立,也不能把文字独立,要连起来分析才行。传统的神经网络做不到这一点。 ※ 传统的神经网络模型,它是有向无环(circle)的/无回路的,就是在隐藏层中各个神经元之间是没有联系的,而实际上我们的大脑并不是这样运作的,所以有了RNN模型,它的隐藏层的各个神经元之间是有相互作用的,能够处理那些输入之间前后有关联的问题。
当前馈神经网络被扩展成包含反馈(feedback)连接/反馈回路时,它们被称为循环神经网络(recurrent neural network)。 前馈神经网络的每个神经元只与前一层的神经元相连, 它接收前一层的输出,并输出给下一层, 各层间没有反馈。
RNN网络的本质特征是在处理单元之间既有内部的反馈连接又有前馈连接(feedforward)。 |
※ 递归神经网络(RNN)是两种人工神经网络的总称。一种是时间递归神经网络(recurrent neural network),另一种是结构递归神经网络(recursive neural network)。时间递归神经网络的神经元间连接构成矩阵,而结构递归神经网络利用相似的神经网络结构递归构造更为复杂的深度网络。RNN一般指代时间递归神经网络。 |
※ 为了捕捉时序数据中的长期依赖关系,为了避免梯度消失(gradient vanishing)和梯度爆炸(gradient explosion), 门控循环单元(GRU)和长短期记忆(LSTM)被广泛应用。
长短期记忆(英语:Long Short-Term Memory,LSTM)是一种时间递归神经网络(RNN), 更确切地说法是一个可以长时间持续的短期记忆模型(a model for the short-term memory which can last for a long period of time)
LSTM通过"门(gate)"让信息选择性通过,从而实现遗忘或记忆的功能。 |
※ LSTM比隐马尔科夫模型(HMM)的表现更好. ※ 就像鱼, 它的记忆只有7秒, 但这种记忆能力是长时间持续的.
※ 梯度消失: 主要是因为网络层数太多,太深,导致梯度无法传播。 ※ 梯度爆炸: 主要是因为梯度太大,所以可以通过减小学习率(梯度变化直接变小)、减小batch size(累积梯度更小)、 features规格化(避免突然来一个大的输入)来优化。 |
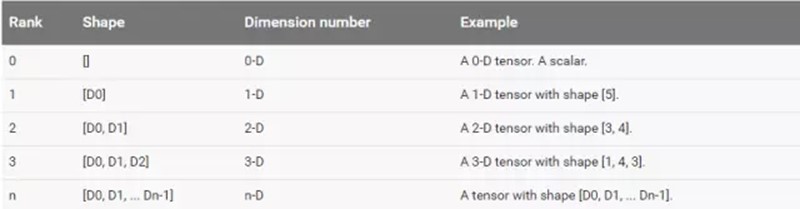
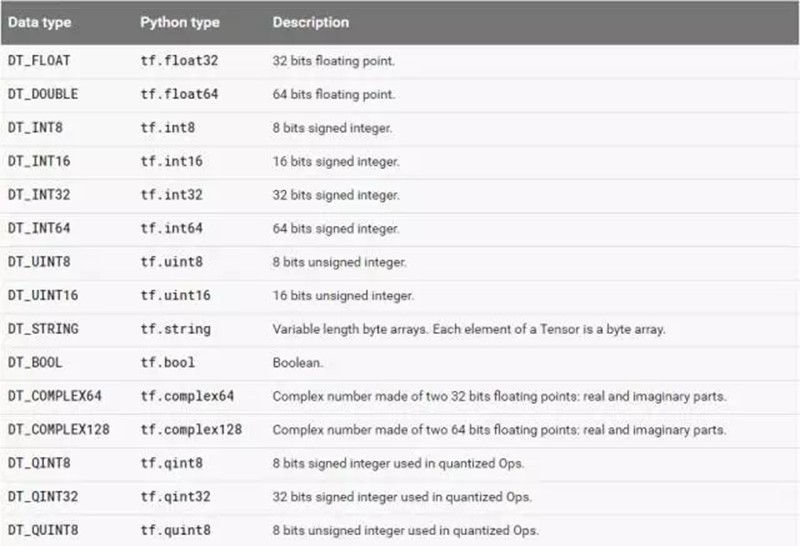
Tensorflow的数据结构有着rank,shape,data types, 的概念: |
(1)rank Rank一般是指数据的维度,其与线性代数中的rank不是一个概念。其常用rank举例如下。
(2)shape
Shape指tensor每个维度数据的个数,可以用python的list/tuple表示。下图表示了rank,shape的关系。
(3)data type Data type,是指单个数据的类型。常用DT_FLOAT,也就是32位的浮点数。下图表示了所有的types。
|
precision ratio(精确率),recall ratio(召回率),accuracy ratio(准确率),F-measure/F-score(精确率P和召回率R的调和平均值) | |||||||||
首先认识四个与其相关参数:
| |||||||||
假如某个班级有男生80人,女生20人,共计100人.目标是找出所有女生. 现在某人挑选出50个人,其中20人是女生,另外还错误的把30个男生也当作女生挑选出来了. 其中:TP=20 FP=30 FN=0 TN=50 精确率=40%, 正确地被检索出来20女生/检索出来的50人) 准确率=70 %, (70 / 100), 70指的是正确地被检索出来的20女 + 正确地未被检索出来的50男生), 召回率=100%, 正确地被检索出来的20女生/(事实的20个女生+ 0 个误判为男生的女生)】 调和平均值= 2 * 0.4 * 1 / (0.4 + 1) = 0.571, 2PR/(P+R), P指精确率, R值召回率 |




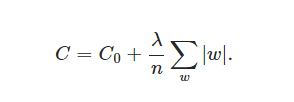
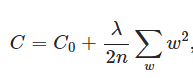
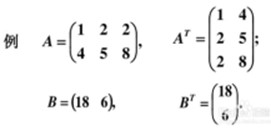

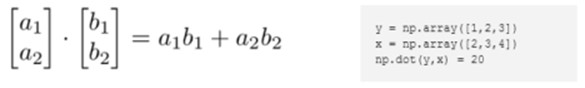
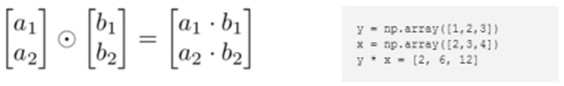

 posted on
posted on

