几个重要数学读法
x趋于C时(经常的情况是"趋于无穷大时"),f(x)的极限是L。 the limit of f of x, as x approaches c, is L ※ f(x) can be made to be as close to L as desired by making x sufficiently close to c. |
f'(x) 或 ※ 导数 f''(x) ※ 二阶导数是斜率变化快慢的反应,表征曲线的凸凹性。 |
|
若z=f(x,y),那么 |
函数f(x)的不定积分 the indefinite integral of f(x)
函数f(x)在a,b的闭区间(即,[a, b])内的定积分 the definite integral of the function of x from a to b |
n元函数
一元函数(function of one variable)的图像y=f(x)在二维坐标里是曲线; 二元函数(function of two variables)的图像z=f(x,y)在三维坐标里是曲面; 三元函数(function of three variables)的图像w=f(x,y,z)在四维坐标里是立体; 只不过因为现实空间是三维的,所以需要一点想像力来想像四维坐标,及坐标里的立体。 |
极限
limit Thus for the limit of a function to exist as the independent variable approaches c , the left-hand and right-hand limits must be equal.
if and only if
※ 如果函数f(x)在自变量x的变化过程中存在极限,即常数A,那么我们可以说f(x)收敛到A,简称f(x)收敛(convergence);否则,称f(x)发散(divergence)。 |
|
|
导数
Derivative The instantaneous rate of change of a function with respect to its variable. 函数随其变量的即时变化率 Derivative is the slope of the tangent line to a function graph, e.g. a curve, at a certain point. Also called differential coefficient ,fluxion 微商/倒数函数图像(如曲线)某一点切线的斜率。
严格定义: 如果函数f(x)在(a,b)中每一点处都可导,则称f(x)在(a,b)上可导,则可建立f(x)的导函数,简称导数,记为f'(x). |
|
微分
differentiation The process of computing a derivative is called differentiation 微分:计算导数的过程
|
|
导数与微分的计算
设 u = u(x),v = v(x)为可导函数,c 是常数,则有:
|
|
|
偏导数/偏微商
partial derivative The derivative with respect to a single variable of a function of two or more variables, regarding other variables as constants. 偏导数/偏微商:多变量函数对其中一个变量的微商,其余变量视作常数.
|
|
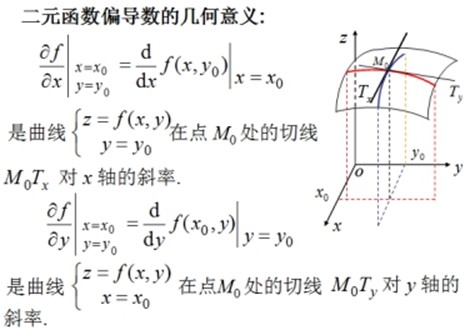
二元函数偏导数的几何意义
过M0点作平面y=y0 / 过M0点作平面x=x0:
|
|
|




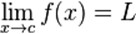

 :
: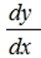 所表示的是一个极限值,而不是两个数量
所表示的是一个极限值,而不是两个数量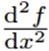

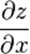
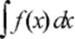
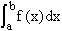
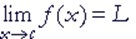


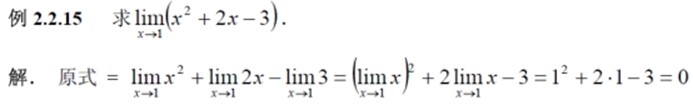
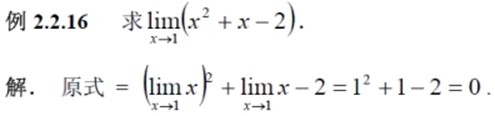













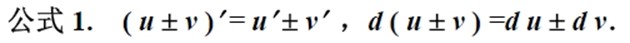

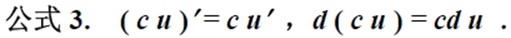
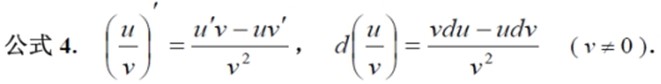









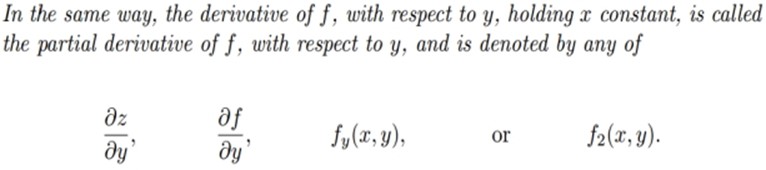








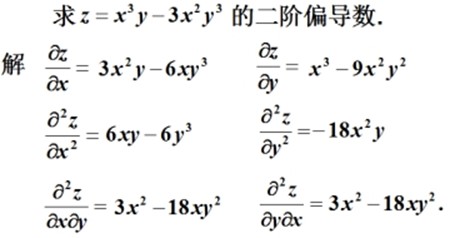
 posted on
posted on

