① 双亲表示法 ② 孩子表示法(其改进为"双亲孩子表示法") ③ 孩子兄弟表示法 |
① 双亲表示法 |
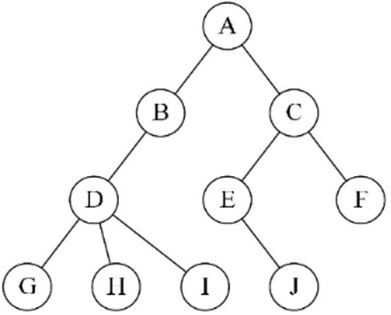
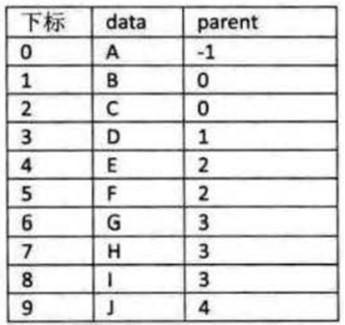
思想: 假设以一组连续空间存储树的结点,同时在每个结点中,附设一个指示器指示其双亲结点在数组中的位置。 数的结点结构:
/* 树的双亲表示法结点结构定义 */ #define MAX_TREE_SIZE 100 typedef int TElemType; /* 树结点的数据类型,目前暂定为整型 */
typedef struct PTNode /* 结点结构 */ { TElemType data; /* 结点数据 */ int parent; /* 双亲位置 */ } PTNode;
typedef struct /* 树结构 */ { PTNode nodes[MAX_TREE_SIZE]; /* 结点数组 */ int r, n; /* 根的位置和结点数 */ } PTree; |
② 孩子表示法 思想: 每个结点有多个指针域,其中每个指针指向一棵子树的根结点,我们把这种方法叫做多重链表表示法 方案一: 每个结点的指针域的个数就等于树的度(缺点: 浪费空间)
方案二: 每个结点指针域的个数等于该结点的度(缺点: 初始化和维护起来难度大)
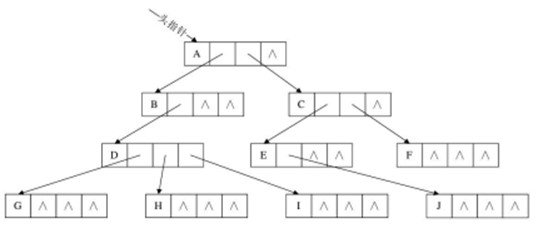
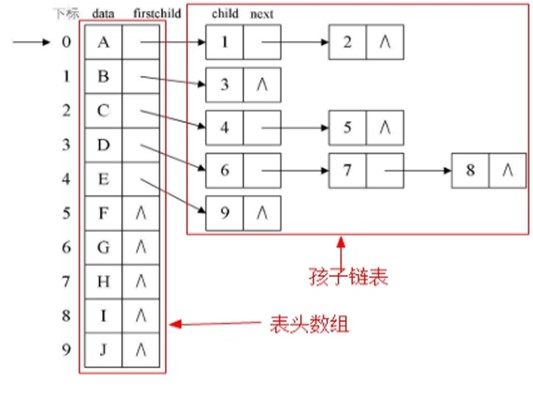
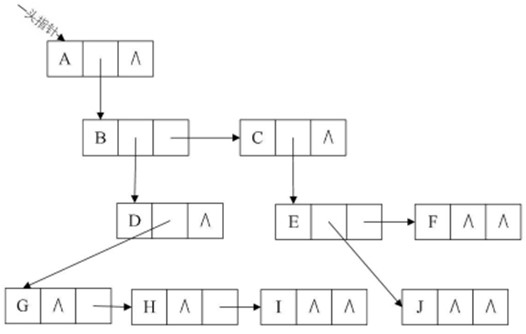
方案三: 针对上述两个方案缺点改进的孩子表示法 思想: 把每个结点的孩子结点排列起来,以单链表作存储结构,则n个结点有n个孩子链表,如果是叶子结点则此单链表为空。然后n个头指针又组成一个线性表,采用顺序存储结构,存放进一个一维数组中. 改进的孩子表示法有两种结点结构:
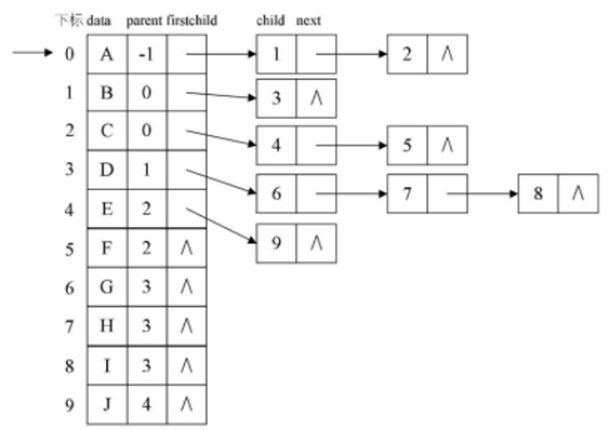
※ 方案三还有一种改进, 就是在表头结点里加一个存放双亲下标的成员, 如上面的右图所示, 这就是进一步完善的"双亲孩子表示法". |
/* 双亲孩子表示法的结构定义 */ #define MAX_TREE_SIZE 100
typedef struct CTNode /* 孩子链表的孩子结点 */ { int child; //孩子节点的下标 struct CTNode *next; //指向下一个孩子节点的指针 } *ChildPtr;
typedef struct /*表头数组的表头结点 */ { TElemType data; int parent; //存放双亲的下标 ChildPtr firstchild; } CTBox;
typedef struct /* 整个树的结构 */ { CTBox nodes[MAX_TREE_SIZE]; /* 表头结点组成的表头数组 */ int r,n; /* r:根的下标; n: 结点数 / } CTree; |
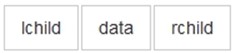
思想: 任意一棵树,它的结点的第一个孩子如果存在就是唯一的,它的右兄弟如果存在也是唯一的。因此,我们设置两个指针,分别指向该结点的第一个孩子和此结点的右兄弟:
|
/* 树的孩子兄弟表示法结构定义 */ typedef struct CSNode { TElemType data; struct CSNode *firstchild, *rightsib; } CSNode, *CSTree; |
//起始部分 |
#include "stdio.h" #include "stdlib.h" #include "io.h" #include "math.h" #include "time.h"
#define OK 1 #define ERROR 0 #define TRUE 1 #define FALSE 0
#define MAXSIZE 100 /* 存储空间初始分配量 */ #define MAX_TREE_SIZE 100 /* 二叉树的最大结点数 */
typedef int Status; /* Status是函数的类型,其值是函数结果状态代码,如OK等 */ typedef int TElemType; /* 树结点的数据类型,目前暂定为整型 */ typedef TElemType SqBiTree[MAX_TREE_SIZE]; /* 0号单元存储根结点; SqBiTree(Sequential BiTree) */ /* 例如:SqBiTree bt; 意味着: TELemtype bt[100]; 即int bt[100] */ |
//定义一个Position结构体, 成员包括某结点所在的层次以及所在层次的序号 |
typedef struct { int level,order; /* 结点的层,本层序号(按满二叉树计算) */ }Position;
TElemType Nil=0; /* 设整型以0为空 */ |
//打印各结点数据域的内容 |
Status visit(TElemType c) { printf("%d ",c); return OK; } |
/* 构造空二叉树T。因为T是固定数组,不会改变,故不需要写成&T */ |
Status InitBiTree(SqBiTree T) //下面的操作是: 传入一个顺序结构存储的树T, 然后打印树的各个结点的值 { int i; for(i=0;i<MAX_TREE_SIZE;i++) T[i]=Nil; /* 初值为0 */ return OK; } |
/* 构造顺序存储的二叉树T, 这里按层序遍历的次序输入二叉树中各个结点的值(字符型或整型) */ |
Status CreateBiTree(SqBiTree T) { int i=0; while(i<10) //下面是通过循环的方式给树的各节点赋值 { T[i]=i+1;
if(i!=0&&T[(i+1)/2-1]==Nil&&T[i]!=Nil) /* i!=0表示此结点(不空), T[(i+1)/2-1]==Nil表示无父节, T[i]!=Nil表示不是根 */ { printf("出现无父节点的非根结点%d\n",T[i]); exit(ERROR); } i++; } while(i<MAX_TREE_SIZE) { T[i]=Nil; /* 将空赋值给T的后面的结点 */ i++; }
return OK; } |
/* 初始条件: 二叉树T存在 */ /* 操作结果: 若T为空二叉树,则返回TRUE,否则FALSE */ |
#define ClearBiTree InitBiTree /* 在顺序存储结构中,两函数完全一样 */
Status BiTreeEmpty(SqBiTree T) { if(T[0]==Nil) /* 根结点为空,则树空 */ return TRUE; else return FALSE; } |
/* 初始条件: 二叉树T存在。操作结果: 返回T的深度 */ |
//注意, i代表结点的个数, j代表T的深度, 一个满二叉树每层的分数为2的(n-1)次幂 int BiTreeDepth(SqBiTree T) { int i,j=-1; for(i=MAX_TREE_SIZE-1;i>=0;i--) /* 找到最后一个结点 */ if(T[i]!=Nil) break; i++; do j++; while(i>=powl(2,j));/* 计算2的j次幂 */ return j; } |
/* 初始条件: 二叉树T存在 */ /* 操作结果: 当T不空,用e返回T的根,返回OK;否则返回ERROR,e无定义 */ |
Status Root(SqBiTree T,TElemType *e) { if(BiTreeEmpty(T)) /* T空 */ return ERROR; else { *e=T[0]; return OK; } } |
/* 初始条件: 二叉树T存在,e是T中某个结点(的位置) */ /* 操作结果: 返回处于位置e(层,本层序号)的结点的值 */ |
TElemType Value(SqBiTree T,Position e) { return T[(int)powl(2,e.level-1)+e.order-2]; } |
/* 初始条件: 二叉树T存在,e是T中某个结点(的位置) */ /* 操作结果: 给处于位置e(层,本层序号)的结点赋新值value */ |
Status Assign(SqBiTree T,Position e,TElemType value) { int i=(int)powl(2,e.level-1)+e.order-2; /* 将层、本层序号转为矩阵的序号 */ if(value!=Nil&&T[(i+1)/2-1]==Nil) /* 给叶子赋非空值但双亲为空 */ return ERROR; else if(value==Nil&&(T[i*2+1]!=Nil||T[i*2+2]!=Nil)) /* 给双亲赋空值但有叶子(不空) */ return ERROR; T[i]=value; return OK; } |
/* 初始条件: 二叉树T存在,e是T中某个结点 */ /* 操作结果: 若e是T的非根结点,则返回它的双亲,否则返回"空" */ |
TElemType Parent(SqBiTree T,TElemType e) { int i; if(T[0]==Nil) /* 空树 */ return Nil; for(i=1;i<=MAX_TREE_SIZE-1;i++) if(T[i]==e) /* 找到e */ return T[(i+1)/2-1]; return Nil; /* 没找到e */ } |
/* 初始条件: 二叉树T存在,e是T中某个结点 */ /* 操作结果: 返回e的左孩子。若e无左孩子,则返回"空" */ |
TElemType LeftChild(SqBiTree T,TElemType e) { int i; if(T[0]==Nil) /* 空树 */ return Nil; for(i=0;i<=MAX_TREE_SIZE-1;i++) if(T[i]==e) /* 找到e */ return T[i*2+1]; return Nil; /* 没找到e */ } |
/* 初始条件: 二叉树T存在,e是T中某个结点 */ /* 操作结果: 返回e的右孩子。若e无右孩子,则返回"空" */ |
TElemType RightChild(SqBiTree T,TElemType e) { int i; if(T[0]==Nil) /* 空树 */ return Nil; for(i=0;i<=MAX_TREE_SIZE-1;i++) if(T[i]==e) /* 找到e */ return T[i*2+2]; return Nil; /* 没找到e */ } |
/* 初始条件: 二叉树T存在,e是T中某个结点 */ /* 操作结果: 返回e的左兄弟。若e是T的左孩子或无左兄弟,则返回"空" */ |
TElemType LeftSibling(SqBiTree T,TElemType e) { int i; if(T[0]==Nil) /* 空树 */ return Nil; for(i=1;i<=MAX_TREE_SIZE-1;i++) if(T[i]==e&&i%2==0) /* 找到e且其序号为偶数(是右孩子) */ return T[i-1]; return Nil; /* 没找到e */ } |
/* 初始条件: 二叉树T存在,e是T中某个结点 */ /* 操作结果: 返回e的右兄弟。若e是T的右孩子或无右兄弟,则返回"空" */ |
TElemType RightSibling(SqBiTree T,TElemType e) { int i; if(T[0]==Nil) /* 空树 */ return Nil; for(i=1;i<=MAX_TREE_SIZE-1;i++) if(T[i]==e&&i%2) /* 找到e且其序号为奇数(是左孩子) */ return T[i+1]; return Nil; /* 没找到e */ } |
/* PreOrderTraverse()调用 */ |
void PreTraverse(SqBiTree T,int e) { visit(T[e]); if(T[2*e+1]!=Nil) /* 左子树不空 */ PreTraverse(T,2*e+1); if(T[2*e+2]!=Nil) /* 右子树不空 */ PreTraverse(T,2*e+2); } |
/* 初始条件: 二叉树存在 */ /* 操作结果: 先序遍历T。 */ |
Status PreOrderTraverse(SqBiTree T) { if(!BiTreeEmpty(T)) /* 树不空 */ PreTraverse(T,0); printf("\n"); return OK; } |
/* InOrderTraverse()调用 */ |
void InTraverse(SqBiTree T,int e) { if(T[2*e+1]!=Nil) /* 左子树不空 */ InTraverse(T,2*e+1); visit(T[e]); if(T[2*e+2]!=Nil) /* 右子树不空 */ InTraverse(T,2*e+2); } |
/* 初始条件: 二叉树存在 */ /* 操作结果: 中序遍历T。 */ |
Status InOrderTraverse(SqBiTree T) { if(!BiTreeEmpty(T)) /* 树不空 */ InTraverse(T,0); printf("\n"); return OK; } |
/* PostOrderTraverse()调用 */ |
void PostTraverse(SqBiTree T,int e) { if(T[2*e+1]!=Nil) /* 左子树不空 */ PostTraverse(T,2*e+1); if(T[2*e+2]!=Nil) /* 右子树不空 */ PostTraverse(T,2*e+2); visit(T[e]); } |
/* 初始条件: 二叉树T存在 */ /* 操作结果: 后序遍历T。 */ |
Status PostOrderTraverse(SqBiTree T) { if(!BiTreeEmpty(T)) /* 树不空 */ PostTraverse(T,0); printf("\n"); return OK; } |
/* 层序遍历二叉树 */ |
void LevelOrderTraverse(SqBiTree T) { int i=MAX_TREE_SIZE-1,j; while(T[i]==Nil) i--; /* 找到最后一个非空结点的序号 */ for(j=0;j<=i;j++) /* 从根结点起,按层序遍历二叉树 */ if(T[j]!=Nil) visit(T[j]); /* 只遍历非空的结点 */ printf("\n"); } |
/* 逐层、按本层序号输出二叉树 */ |
void Print(SqBiTree T) { int j,k; Position p; TElemType e; for(j=1;j<=BiTreeDepth(T);j++) { printf("第%d层: ",j); for(k=1;k<=powl(2,j-1);k++) { p.level=j; p.order=k; e=Value(T,p); if(e!=Nil) printf("%d:%d ",k,e); } printf("\n"); } } |
//主函数 |
int main() { Status i; Position p; TElemType e; SqBiTree T; InitBiTree(T); CreateBiTree(T); printf("建立二叉树后,树空否?%d(1:是 0:否) 树的深度=%d\n",BiTreeEmpty(T),BiTreeDepth(T)); i=Root(T,&e); if(i) printf("二叉树的根为:%d\n",e); else printf("树空,无根\n"); printf("层序遍历二叉树:\n"); LevelOrderTraverse(T); printf("前序遍历二叉树:\n"); PreOrderTraverse(T); printf("中序遍历二叉树:\n"); InOrderTraverse(T); printf("后序遍历二叉树:\n"); PostOrderTraverse(T); printf("修改结点的层号3本层序号2。"); p.level=3; p.order=2; e=Value(T,p); printf("待修改结点的原值为%d请输入新值:50 ",e); e=50; Assign(T,p,e); printf("前序遍历二叉树:\n"); PreOrderTraverse(T); printf("结点%d的双亲为%d,左右孩子分别为",e,Parent(T,e)); printf("%d,%d,左右兄弟分别为",LeftChild(T,e),RightChild(T,e)); printf("%d,%d\n",LeftSibling(T,e),RightSibling(T,e)); ClearBiTree(T); printf("清除二叉树后,树空否?%d(1:是 0:否) 树的深度=%d\n",BiTreeEmpty(T),BiTreeDepth(T)); i=Root(T,&e); if(i) printf("二叉树的根为:%d\n",e); else printf("树空,无根\n");
return 0; }
|
//起始部分 |
#include "string.h" #include "stdio.h" #include "stdlib.h" #include "io.h" #include "math.h" #include "time.h"
#define OK 1 #define ERROR 0 #define TRUE 1 #define FALSE 0
#define MAXSIZE 100 /* 存储空间初始分配量 */
typedef int Status; /* Status是函数的类型,其值是函数结果状态代码,如OK等 */ |
/* 用于构造二叉树 */ |
int index=1; typedef char String[24]; /* 0号单元存放串的长度 */ String str; //相当于char str[24]
Status StrAssign(String T,char *chars) //字符串相互赋值的函数 { int i; if(strlen(chars)>MAXSIZE) return ERROR; else { T[0]=strlen(chars); for(i=1;i<=T[0];i++) T[i]=*(chars+i-1); return OK; } } |
//访问结点的值 |
typedef char TElemType;
TElemType Nil=' '; /* 字符型以空格符为空 */
Status visit(TElemType e) { printf("%c ",e); return OK; } |
//二叉树的二叉链表的结点结构的定义:
|
typedef struct BiTNode /* 结点结构 */ { TElemType data; /* 结点数据 */ struct BiTNode *lchild,*rchild; /* 左右孩子指针 */ }BiTNode,*BiTree; //BiTNode代表结点, BiTree代表树 |
/* 构造空二叉树T */ |
Status InitBiTree(BiTree *T) { *T=NULL; return OK; } |
/* 初始条件: 二叉树T存在。操作结果: 销毁二叉树T */ |
void DestroyBiTree(BiTree *T) { if(*T) { if((*T)->lchild) /* 有左孩子 */ DestroyBiTree(&(*T)->lchild); /* 销毁左孩子子树 */ if((*T)->rchild) /* 有右孩子 */ DestroyBiTree(&(*T)->rchild); /* 销毁右孩子子树 */ free(*T); /* 释放根结点 */ *T=NULL; /* 空指针赋0 */ } } |
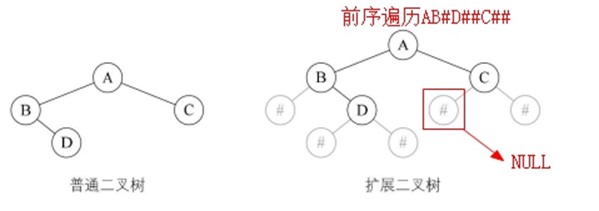
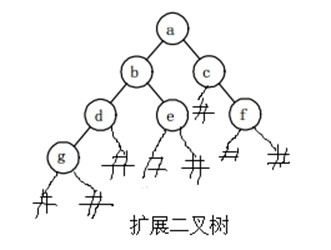
/* 按前序输入二叉树中结点的值(一个字符) */ /* #表示空树,构造二叉链表表示二叉树T。 */ //为了能让每个结点确认是否有左右孩子,我们对它进行了扩展, 即是将二叉树中每个结点的空指针引出一个虚结点,其值为一特定值,比如"#":
|
void CreateBiTree(BiTree *T) { TElemType ch;
/* scanf("%c",&ch); */ ch=str[index++];
if(ch=='#') *T=NULL; else //如果ch!=#, 那么就生成一个新结点 { *T=(BiTree)malloc(sizeof(BiTNode)); //sizeof(BiTNode)得到的是结构体的大小 if(!*T) //相当于if(T==0) exit(OVERFLOW); (*T)->data=ch; /* 生成根结点的数据 */ CreateBiTree(&(*T)->lchild); /* 构造左子树 */ CreateBiTree(&(*T)->rchild); /* 构造右子树 */ } } |
/* 初始条件: 二叉树T存在 */ /* 操作结果: 若T为空二叉树,则返回TRUE,否则FALSE */ |
Status BiTreeEmpty(BiTree T) { if(T) return FALSE; else return TRUE; } |
#define ClearBiTree DestroyBiTree//意思是ClearBiTree()和DestroyBiTree()意思是相同的
/* 初始条件: 二叉树T存在。操作结果: 返回T的深度 */ int BiTreeDepth(BiTree T) { int i,j; if(!T) return 0; if(T->lchild) i=BiTreeDepth(T->lchild); else i=0; if(T->rchild) j=BiTreeDepth(T->rchild); else j=0; return i>j?i+1:j+1; } |
/* 初始条件: 二叉树T存在。操作结果: 返回T的根 */ |
TElemType Root(BiTree T) { if(BiTreeEmpty(T)) return Nil; else return T->data; }
/* 初始条件: 二叉树T存在,p指向T中某个结点 */ /* 操作结果: 返回p所指结点的值 */ TElemType Value(BiTree p) { return p->data; } |
/* 给p所指结点赋值为value */ |
void Assign(BiTree p,TElemType value) { p->data=value; }
/* 初始条件: 二叉树T存在 */ /* 操作结果: 前序递归遍历T */ |
/* 初始条件: 二叉树T存在 */ /* 操作结果: 前序递归遍历T */ |
void PreOrderTraverse(BiTree T) { if(T==NULL) return; printf("%c",T->data);/* 显示结点数据,可以更改为其它对结点操作 */ PreOrderTraverse(T->lchild); /* 再先序遍历左子树 */ PreOrderTraverse(T->rchild); /* 最后先序遍历右子树 */ } |
/* 初始条件: 二叉树T存在 */ /* 操作结果: 中序递归遍历T */ |
void InOrderTraverse(BiTree T) { if(T==NULL) return; InOrderTraverse(T->lchild); /* 中序遍历左子树 */ printf("%c",T->data);/* 显示结点数据,可以更改为其它对结点操作 */ InOrderTraverse(T->rchild); /* 最后中序遍历右子树 */ } |
/* 初始条件: 二叉树T存在 */ /* 操作结果: 后序递归遍历T */ |
void PostOrderTraverse(BiTree T) { if(T==NULL) return; PostOrderTraverse(T->lchild); /* 先后序遍历左子树 */ PostOrderTraverse(T->rchild); /* 再后序遍历右子树 */ printf("%c",T->data);/* 显示结点数据,可以更改为其它对结点操作 */ } |
//主函数 |
int main() { int i; BiTree T; TElemType e1; InitBiTree(&T);
StrAssign(str,"ABDH#K###E##CFI###G#J##");
CreateBiTree(&T);
printf("构造空二叉树后,树空否?%d(1:是 0:否) 树的深度=%d\n",BiTreeEmpty(T),BiTreeDepth(T)); e1=Root(T); printf("二叉树的根为: %c\n",e1);
printf("\n前序遍历二叉树:"); PreOrderTraverse(T); printf("\n中序遍历二叉树:"); InOrderTraverse(T); printf("\n后序遍历二叉树:"); PostOrderTraverse(T); ClearBiTree(&T); printf("\n清除二叉树后,树空否?%d(1:是 0:否) 树的深度=%d\n",BiTreeEmpty(T),BiTreeDepth(T)); i=Root(T); if(!i) printf("树空,无根\n");
return 0; }
|
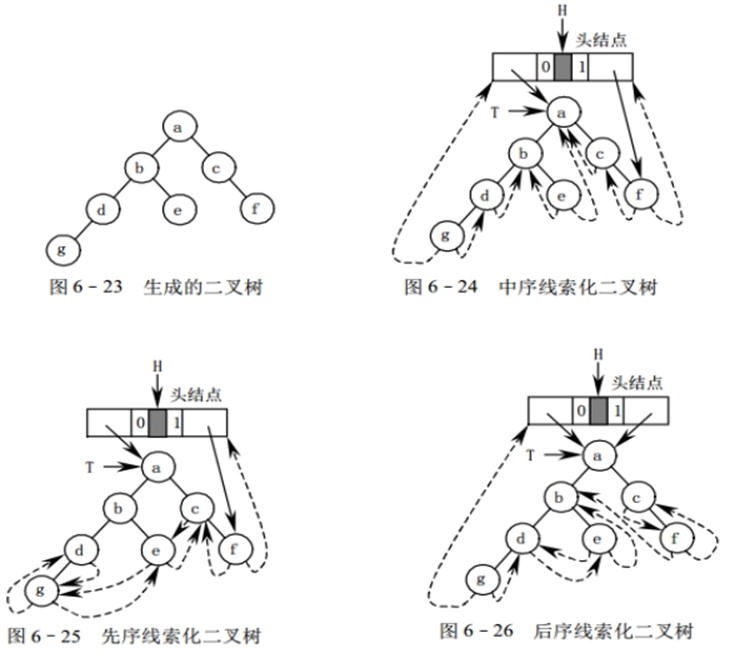
概念: 指向前驱和后继的指针称为线索,加上线索的二叉链表称为线索链表,相应的二叉树就称为线索二叉树(Threaded Binary Tree)。 线索化:对二叉树以某种次序(前, 中, 后)遍历使其变为线索二叉树的过程(即在遍历过程中用线索取代空指针)。
线索链表的结点:
ltag为0时, lchild指向该结点的左孩子,为1时指向该结点的前驱。 rtag为0时, rchild指向该结点的右孩子,为1时指向该结点的后继。
从结点左边出发的线指向该节点的前驱, 从结点右边出发的线指向该节点的后继. 左上图的遍历: 前序遍历: abdgecf 中序遍历: gdbeacf 后序遍历: gdebfca
|
线索化的意义: 从任一结点出发都能快速找到其前驱和后继,且不必借助堆栈。 如果二叉树需要经常遍历, 则采用线索二叉树较好(因为借助线索二叉树遍历二叉树, 无需堆栈/递归算法) |
//起始部分 |
#include "string.h" #include "stdio.h" #include "stdlib.h" #include "io.h" #include "math.h" #include "time.h"
#define OK 1 #define ERROR 0 #define TRUE 1 #define FALSE 0
#define MAXSIZE 100 /* 存储空间初始分配量 */
typedef int Status; /* Status是函数的类型,其值是函数结果状态代码,如OK等 */ typedef char TElemType; typedef enum {Link,Thread} PointerTag; /* Link==0表示指向左右孩子指针, */ /* Thread==1表示指向前驱或后继的线索 */ |
//二叉线索存储结点结构 |
typedef struct BiThrNode /* 二叉线索存储结点结构 */ { TElemType data; /* 结点数据 */ struct BiThrNode *lchild, *rchild; /* 左右孩子指针 */ PointerTag LTag; PointerTag RTag; /* 左右标志 */ } BiThrNode, *BiThrTree;
TElemType Nil='#'; /* 字符型以#符为空 */
Status visit(TElemType e) { printf("%c ",e); return OK; } |
/* 按前序输入二叉线索树中结点的值,构造二叉线索树T */ /* 0(整型)/空格(字符型)表示空结点 */ |
Status CreateBiThrTree(BiThrTree *T) { TElemType h; scanf("%c",&h);
if(h==Nil) *T=NULL; else { *T=(BiThrTree)malloc(sizeof(BiThrNode)); if(!*T) exit(OVERFLOW); (*T)->data=h; /* 生成根结点(前序) */ CreateBiThrTree(&(*T)->lchild); /* 递归构造左子树 */ if((*T)->lchild) /* 有左孩子 */ (*T)->LTag=Link; CreateBiThrTree(&(*T)->rchild); /* 递归构造右子树 */ if((*T)->rchild) /* 有右孩子 */ (*T)->RTag=Link; } return OK; } |
//中序遍历进行中序线索化 |
BiThrTree pre; /* 全局变量,始终指向刚刚访问过的结点 */ /* 中序遍历进行中序线索化 */ void InThreading(BiThrTree p) { if(p) { InThreading(p->lchild); /* 递归左子树线索化 */ if(!p->lchild) /* 如果某结点的左指针域为空 */ { p->LTag=Thread; /* 前驱线索 */ p->lchild=pre; /* 左孩子指针指向前驱 */ } if(!pre->rchild) /* 前驱没有右孩子 */ { pre->RTag=Thread; /* 后继线索 */ pre->rchild=p; /* 前驱右孩子指针指向后继(当前结点p) */ } pre=p; /* 保持pre指向p的前驱 */ InThreading(p->rchild); /* 递归右子树线索化 */ } } |
/* 中序遍历二叉树T,并将其中序线索化,Thrt指向头结点 */ |
Status InOrderThreading(BiThrTree *Thrt,BiThrTree T) { *Thrt=(BiThrTree)malloc(sizeof(BiThrNode)); if(!*Thrt) exit(OVERFLOW); (*Thrt)->LTag=Link; /* 建头结点 */ (*Thrt)->RTag=Thread; (*Thrt)->rchild=(*Thrt); /* 右指针回指 */ if(!T) /* 若二叉树空,则左指针回指 */ (*Thrt)->lchild=*Thrt; else { (*Thrt)->lchild=T; pre=(*Thrt); InThreading(T); /* 中序遍历进行中序线索化 */ pre->rchild=*Thrt; pre->RTag=Thread; /* 最后一个结点线索化 */ (*Thrt)->rchild=pre; } return OK; } |
/* 中序遍历二叉线索树T(头结点)的非递归算法 */ |
Status InOrderTraverse_Thr(BiThrTree T) { BiThrTree p; p=T->lchild; /* p指向根结点 */ while(p!=T) { /* 空树或遍历结束时,p==T */ while(p->LTag==Link) p=p->lchild; if(!visit(p->data)) /* 访问其左子树为空的结点 */ return ERROR; while(p->RTag==Thread&&p->rchild!=T) { p=p->rchild; visit(p->data); /* 访问后继结点 */ } p=p->rchild; } return OK; } |
//主函数 |
int main() { BiThrTree H,T; printf("请按前序输入二叉树(如:'ABDH##I##EJ###CF##G##')\n"); CreateBiThrTree(&T); /* 按前序产生二叉树 */ InOrderThreading(&H,T); /* 中序遍历,并中序线索化二叉树 */ printf("中序遍历(输出)二叉线索树:\n"); InOrderTraverse_Thr(H); /* 中序遍历(输出)二叉线索树 */ printf("\n");
return 0; } |
//上面的程序:
|
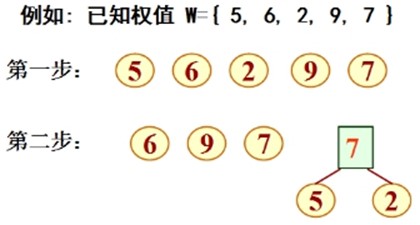
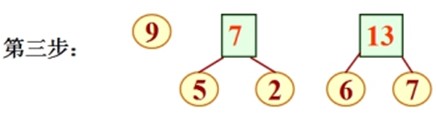
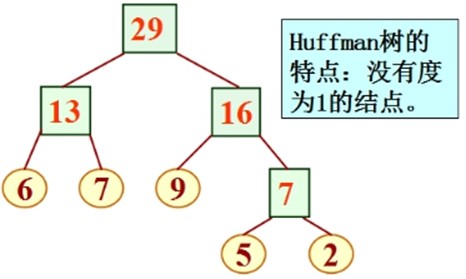
//最优二叉树/Huffman树: 带权路径长度WPL最小的二叉树 //构造Huffman树的基本思想: 权值大的结点用短路径,权值小的结点用长路径。 //构造Huffman树的步骤(即Huffman算法): (1) 由给定的 n 个权值{ w1, w2, …, wn }构成n棵二叉树的集合F = { T1, T2, …, Tn } (即森林) ,其中每棵二叉树 Ti 中只有一个带权为 wi 的根结点,其左右子树均空。 (2) 在F 中选取两棵根结点权值最小的树 做为左右子树构造一棵新的二叉树,且让新二叉树根结点的权值等于其左右子树的根结点权值之和。 (3) 在F 中删去这两棵树,同时将新得到的二叉树加入 F中。 (4) 重复(2) 和(3) , 直到 F 只含一棵树为止。这棵树便是Huffman树。
|
赫夫曼编码属于贪心算法. 贪心算法(又称 贪婪算法)是指,在对问题求解时总是做出在当前看来是最好的选择。不从整体最优上加以考虑,他所做出的仅是在某种意义上的局部 最优解。
文本文件的编码方式: ① 等长编码 假设一个文本文件面存有abcdef六个字符 方案1: 采用ASCII码, 那么对应的二进制应该为: 01100001·01100010·01100011·01100100·01100101·01100110; 方案2: 创建一种新的编码, 如: 000·001·010·011·100·101;
这样,相比ASCII码压缩了近乎3/8, 但是如果我们用普通编辑器打开文件的话,会发现全是乱码,解决方法是a. 开发一个对应编码的编辑器了; b. 保存的时候我们使用新的较短的编码,在读取的时候,再转换成ASCII码.
② 变长编码 在现实中,各个字符在文件里面占有的比例一般是不同的, 例如现在存在一个有100个字符的ASCII码文件,其出现次数分别为:
使用等长编码占用的位数为:(45+13+12+16+9+5)∗3=300
我们采用一种变长编码的形式来重新压缩这个文件,将占有比重大的字符编码变短,将占有比重小的文件编码拉长:
占用的位数为:45∗1+13∗3+12∗3+16∗3+9∗4+5∗4=224,相比于上面的等长编码,大约节省了25%的空间.
③ 前缀码 前缀码设计原则: 没有任何码字是其他码字的前缀 由哈夫曼树求得的编码为最优前缀码.
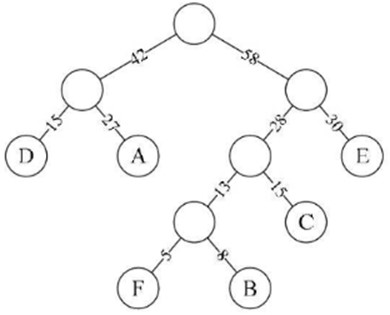
假设六个字母的频率为A 27,B 8,C 15,D15,E 30,F 5,合起来是100%, 我们完全可以重新按照赫夫曼树来规划它们。
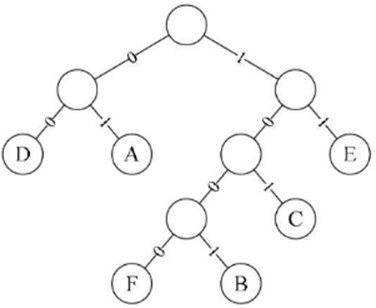
左图为构造赫夫曼树的过程的权值显示。右图为将权值左分支改为0,右分支改为1后的赫夫曼树。 我们对这六个字母用其从树根到叶子所经过路径的0或1来编码,可以得到如下编码:
将文字内容为"BADCADFEED"再次编码,对比可以看到结果串变小了: 等长编码二进制串:001000011010000011101100100011(共30个字符) 赫夫曼编码二进制串:1001010010101001000111100(共25个字符)
|
//赫夫曼编码的实现
|
#include <stdio.h> #include <limits.h> #include <stdlib.h> #include <string.h>
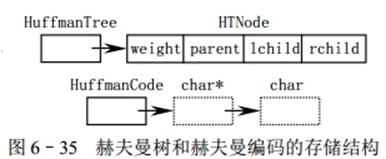
typedef struct { unsigned int weight; unsigned int parent,lchild,rchild; }HTNode,*HuffmanTree; // 动态分配数组存储赫夫曼树 typedef char **HuffmanCode; // 动态分配数组存储赫夫曼编码表 |
// 返回i个结点中权值最小的树的根结点序号,该函数将由下面的select()函数调用 |
int min(HuffmanTree t,int i) { int j,flag; unsigned int k=UINT_MAX; // 取k为不小于可能的值(无符号整型最大值) for(j=1;j<=i;j++) if(t[j].weight<k&&t[j].parent==0) // t[j] 是树的根结点 k=t[j].weight,flag=j; t[flag].parent=1; // 给选中的根结点的双亲赋1,避免第2次查找该结点 return flag; } |
// 在i个结点中选择2个权值最小的树的根结点序号, s1为其中序号小的那个 |
void select(HuffmanTree t,int i,int &s1,int &s2) { int j; s1=min(t,i); s2=min(t,i); if(s1>s2) { j=s1; s1=s2; s2=j; } } |
// w存放n个字符的权值(均>0) ,构造赫夫曼树HT,并求出n个字符的赫夫曼编码HC |
void HuffmanCoding(HuffmanTree &HT,HuffmanCode &HC,int *w,int n) // 算法 6.12 { int m,i,s1,s2,start; unsigned c,f; HuffmanTree p; char *cd; if(n<=1) return; m=2*n-1; HT=(HuffmanTree)malloc((m+1)*sizeof(HTNode)); // 0号单元未用 for(p=HT+1,i=1;i<=n;++i,++p,++w) { (*p).weight=*w; (*p).parent=0; (*p).lchild=0; (*p).rchild=0; } for(;i<=m;++i,++p) (*p).parent=0; for(i=n+1;i<=m;++i) // 建赫夫曼树 { // 在 HT[1~ i-1] 中选择 parent为 0且 weight最小的两个结点,其序号分别为 s1和 s2 select(HT,i-1,s1,s2); HT[s1].parent=HT[s2].parent=i; HT[i].lchild=s1; HT[i].rchild=s2; HT[i].weight=HT[s1].weight+HT[s2].weight; } // 从叶子到根逆向求每个字符的赫夫曼编码 HC=(HuffmanCode)malloc((n+1)*sizeof(char*)); // 分配 n个字符编码的头指针向量 ([0] 不用 ) cd=(char*)malloc(n*sizeof(char)); // 分配求编码的工作空间 cd[n-1]='\0'; // 编码结束符 for(i=1;i<=n;i++) { // 逐个字符求赫夫曼编码 start=n-1; // 编码结束符位置 for(c=i,f=HT[i].parent;f!=0;c=f,f=HT[f].parent) // 从叶子到根逆向求编码 if(HT[f].lchild==c) cd[--start]='0'; else cd[--start]='1'; HC[i]=(char*)malloc((n-start)*sizeof(char)); // 为第 i个字符编码分配空间 strcpy(HC[i],&cd[start]); // 从 cd复制编码 (串 ) 到 HC } free(cd); // 释放工作空间 } |
//主函数 |
void main() { HuffmanTree HT; HuffmanCode HC; int *w,n,i; printf("请输入权值的个数 (>1): "); scanf("%d",&n); w=(int*)malloc(n*sizeof(int)); printf("请依次输入 %d个权值 (整型 ):\n",n); for(i=0;i<=n-1;i++) scanf("%d",w+i); HuffmanCoding(HT,HC,w,n); for(i=1;i<=n;i++) puts(HC[i]); }
|










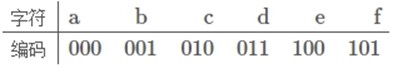




 posted on
posted on
