OO第一单元总结

基于度量来分析自己的程序结构

第一次作业与第二次作业我采用的架构基本相同，都没有涉及到组合与求导的分离，第三次则进行了重构，实现了这一点。
基于此我度量类的属性个数、方法个数、每个方法规模、每个方法的控制分支数目、类总代码规模，并计算了经典的OO度量
，分析类的内聚和相互间的耦合情况，具体指标如下

Complexity Metrics（复杂度分析）

这部分我们需要使用的主要是方法和类的复杂度分析。
方法的复杂度分析主要基于循环复杂度的计算。循环复杂度是一种表示程序复杂度的软件度量，由程序流程图中的“基础路径”数量得来。

1. ev(G)：即Essentail Complexity，用来表示一个方法的结构化程度，范围在[1,v(G)]之间，值越大则程序的结构越“病态”，其计算过程和图的“缩点”有关。
2. iv(G)：即Design Complexity，用来表示一个方法和他所调用的其他方法的紧密程度，范围也在[1,v(G)]之间，值越大联系越紧密。
3. v(G)：即循环复杂度，可以理解为穷尽程序流程每一条路径所需要的试验次数。

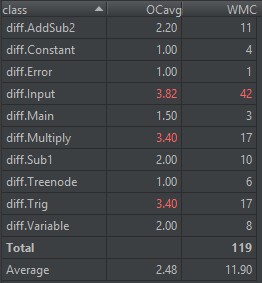
对于类，有OCavg和WMC两个项目。

1. OCavg：类的方法的平均循环复杂度。
2. WNC：类的方法的总循环复杂度。

Dependency Metrics（依赖度分析)

1. Cyclic：指和类直接或间接相互依赖的类的数量。这样的相互依赖可能导致代码难以理解和测试。
2. Dcy和Dcy：计算了该类直接依赖的类的数量，带表示包括了间接依赖的类。
3. Dpt和Dpt：计算了直接依赖该类的类的数量，带表示包括了间接依赖的类。

第二次作业

类图如下所示，没有使用任何继承与接口特性。

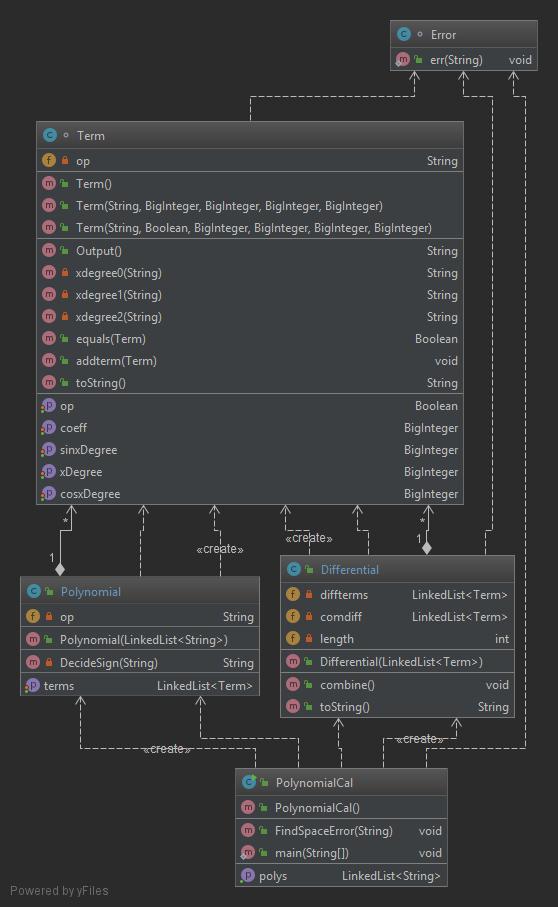
度量表如下所示

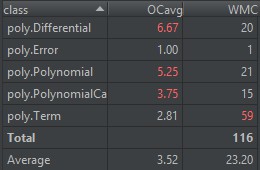
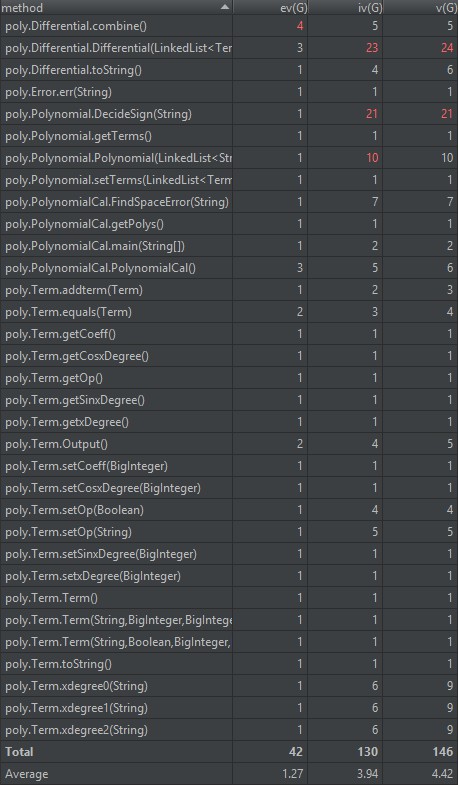
第三次作业

这次作业在之前基础上重构，使用了继承机制，并且严格将组合逻辑与求导方法分离，将接口与实现分离。
本次作业采用编译原理中的递归子程序法读入数据，保存为一棵表达式数，然后对这棵树进行递归求导。
具体见如下类图

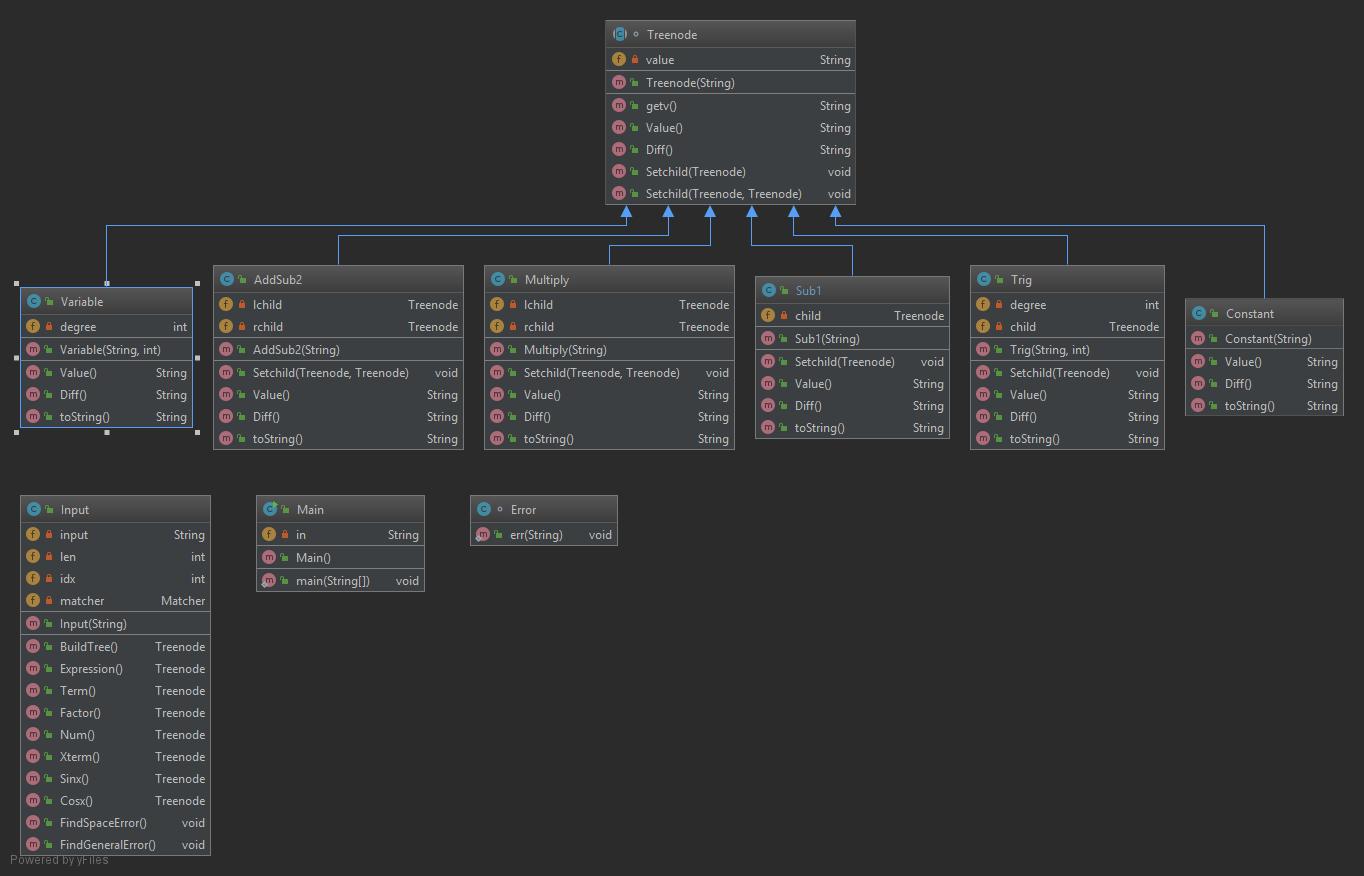
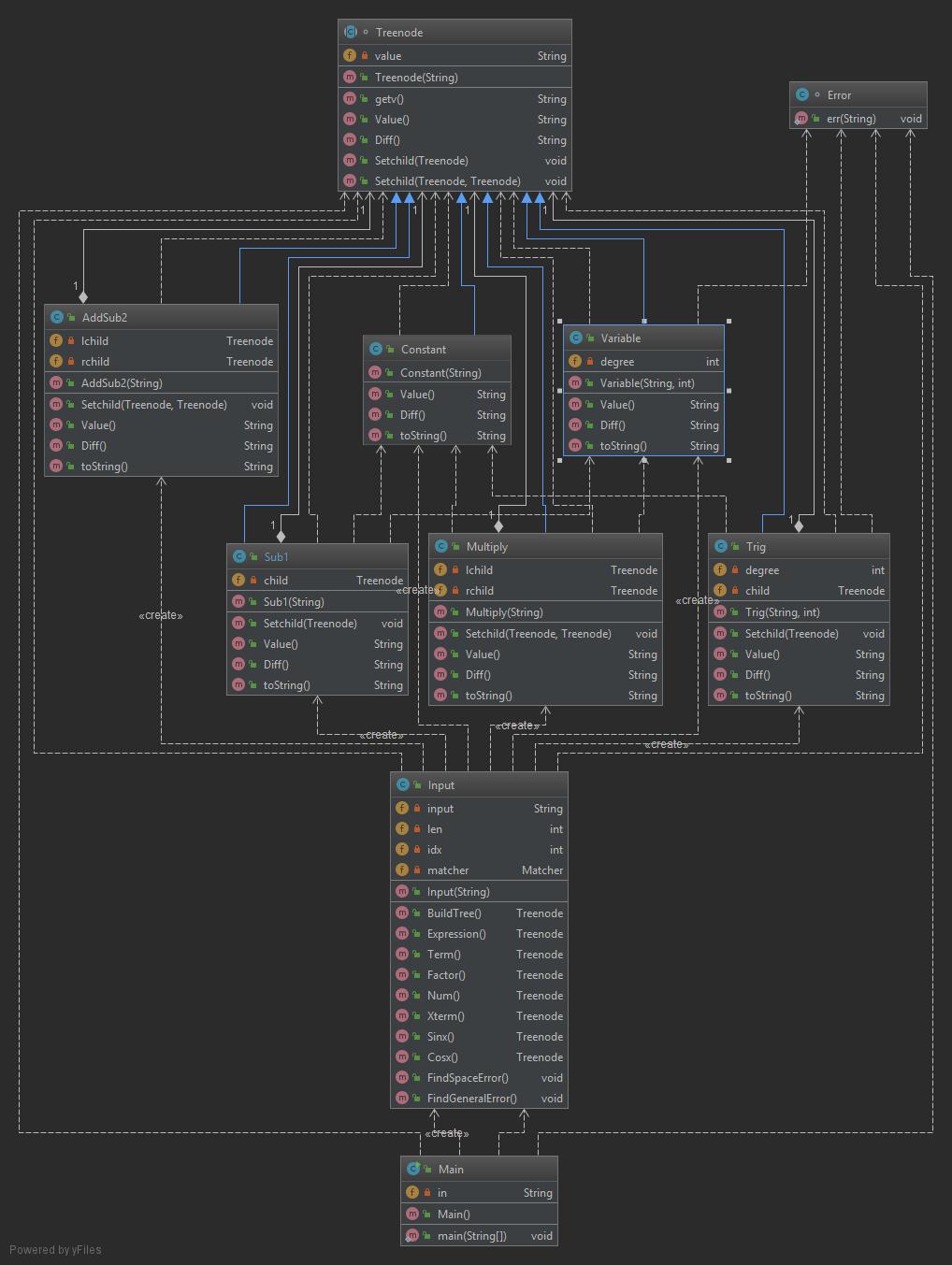
度量表如下所示

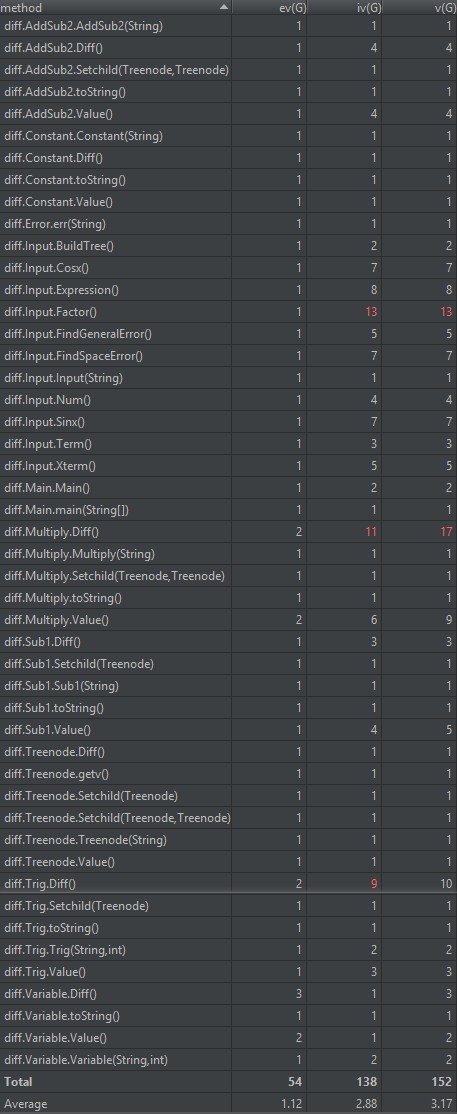
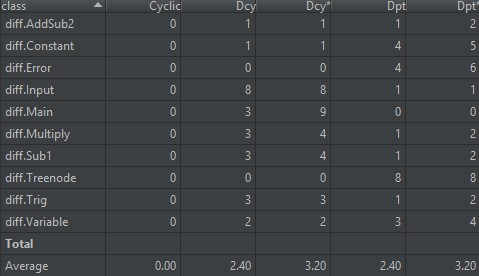
BUG分析

第一次作业

主要bug在于没有处理大数计算，没有用到BigInteger类，由此导致在整形溢出时会陷入异常

第二次作业

主要在于优化表达式的时候条件考虑不清楚，导致优化后的结果反而错误

第三次作业

主要在于优化表达式的时候条件考虑不清楚，导致优化后的结果反而错误

Applying Creational Pattern

面向过程的思维是一次性处理所有的输入数据，判断格式，构建数据容器存储数据，求导，相加，输出……繁冗的细节决定了面向过程思想必然不能解决问题；
然而用面向对象的思想就应该是，因子分类，共同继承一个抽象类factor，项是由因子组成的链表；表达式看成是项组成的列表。如此层层递进，数据的存储将
变得十分简便。在前两次作业中，我没有体会到面向对象的特性，将所有项都归为了 x^n1*sinn2*cos^n3 的形式，但是这种做法在第三次作业中完全不具备
可拓展性。因此我重构了所有方法，创建出单独的sin，cos和x的幂次这三个基本类，然后创建出加法乘法与嵌套三重规则，针对不同的情况各自独立的实
现求导规则，然后由一颗表达式树串在一起，即可实现递归求导。以后会继续努力，继续体会OO的思想，减少面向过程编程的想法。