BUAA OO 第一单元总结与反思
BUAA OO 第一单元总结与反思
写在前面
本篇博客重点对三次作业进行需求分析,并在此基础上给出架构方案设计、代码结构分析与测试思路,最后讲述了自己在完成三次作业后的整体感受与体会。
尽管我在第一次作业花费了多日思考且无从下手,但也正是由于我在第一次作业中采用了助教推荐的递归下降算法进行表达式的解析,并且在架构的过程中注重考虑了可拓展性,因此本单元并未进行代码的重构,三次作业所花费的时间也是依次递减的。
第一次作业
需求分析
本次作业要求我们能够读入一个包含加、减、乘、乘方(**)以及括号(其中括号的深度至多为 1 层)的单变量表达式,表达式的规范由形式化表述进行限定,最终输出恒等变形展开所有括号后的表达式。
在参考了许多资料,经过长时间思考后,我首先对读入的表达式进行预处理,去除空白字符和连续符号,然后将表达式分为Expr->Term->Factors三个层级,表达式包含项,项包含因子,因子分为表达式因子和常数/x因子,而表达式因子又可以分为多个项......如此递归下降,直至全部分解成常数/x因子为止,即可完成解析。(细细思考一下不难发现,这样的设计已经可以满足多层括号嵌套的计算化简了。)
架构方案设计
考虑到设计的层次性、可拓展性已经后续作业可能出现的各种功能需求,我采取了编译中常见的递归下降算法来作为解析表达式的核心逻辑,这一底层核心架构也贯穿了整个三次作业。
本次作业的UML类图如下所示:
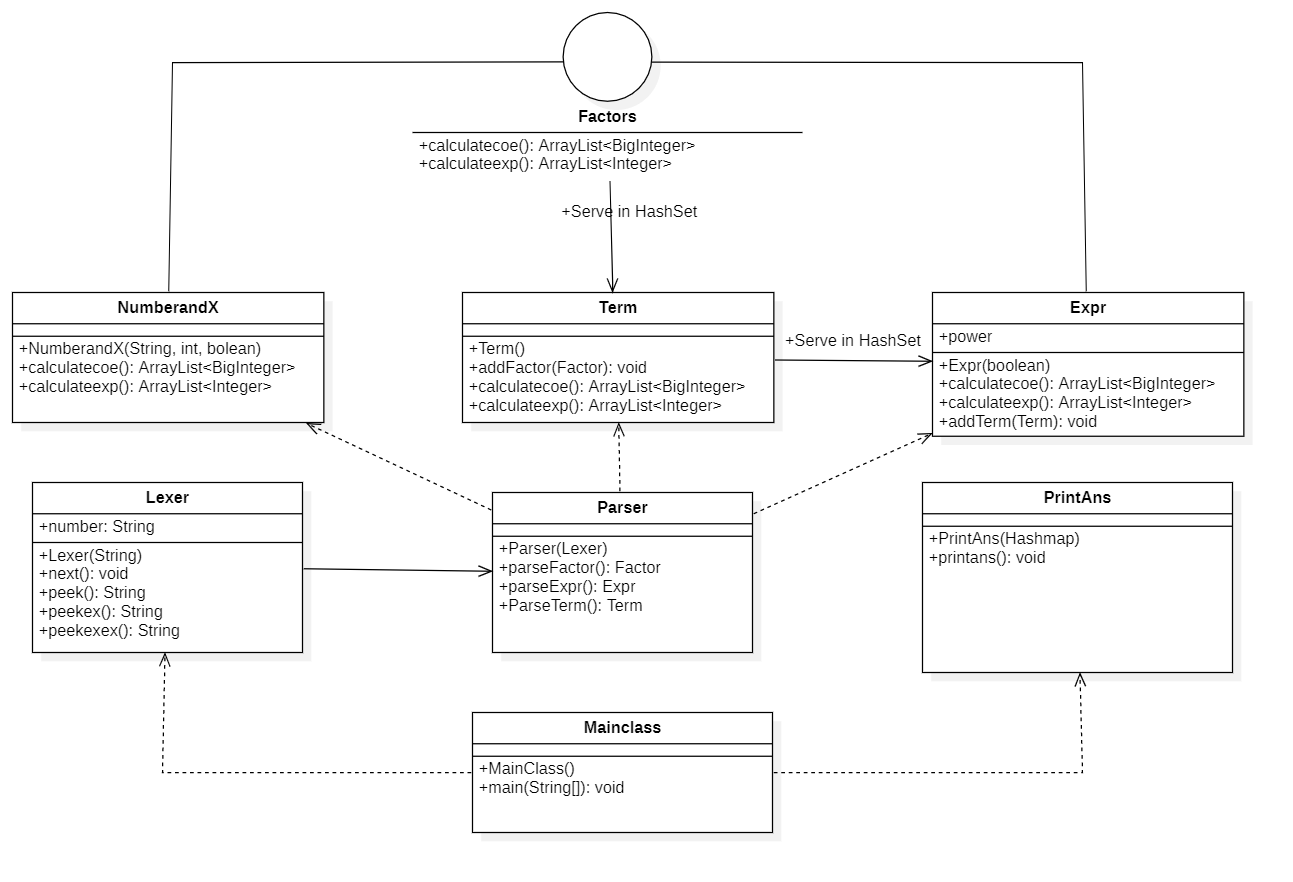
在我们的解析工作完成之后,我们的表达式树所有的叶子节点都是数字/x因子,此时我们不难想到用一个统一的表达形式ax^b来表达一个因子,即对于每个因子由数对<a,b>来唯一确定,再考虑到合并同类项的实现,使用HashMap这一数据结构来存储就显得理所应当了。
输出优化策略
- x ** 2 --> x * x
- 当存在系数为正的项时,任选其一放在第一个输出
当我们做到以上两点时,我相信本次作业的性能分一定能拿满了!
代码结构分析
首先从类的维度来分析:
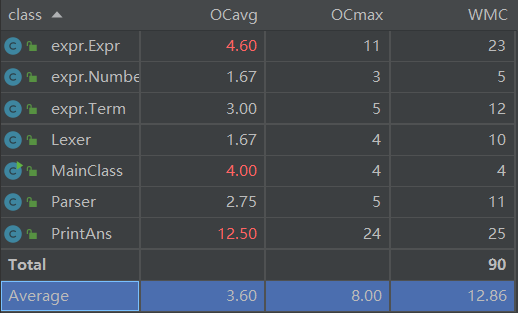
对于这三个评价标准的理解如下:
- 3:代表类的方法的平均循环复杂度。
- OCmax:代表类的方法的最高循环复杂度。
- WMC:代表类的总循环复杂度。
然后我们从更细分的方法维度来分析:
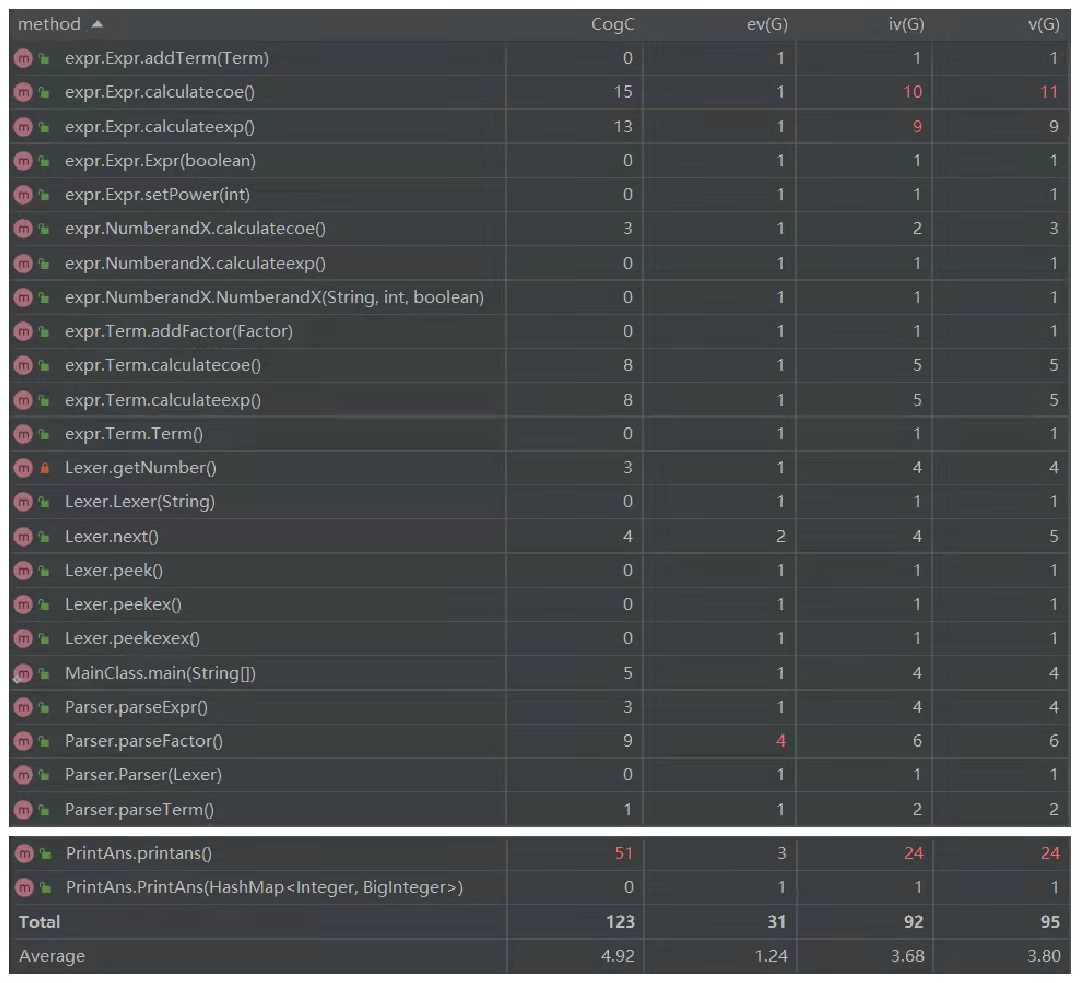
首先对一下表格中的评价标准进行解释:
- ev(G):基本复杂度,是用来衡量程序非结构化程度的。
- Iv(G):模块设计复杂度,是用来衡量模块判定结构,即模块和其他模块的调用关系。
- v(G):模块判定结构复杂度,数量上表现为独立路径的条数。
- CogC:认知复杂度。
整体来看,除了类PrintAns中的printans()方法在复杂度上一骑绝尘远远甩开其他方法之外,整体的复杂度较为均衡且比较低,基本符合了设计的思想。下面让我们单独来看看这个方法。
public void printans() {
StringBuilder anss = new StringBuilder();
//第一项输出正数
for (Integer i : ans.keySet()) {
if (ans.get(i).compareTo(BigInteger.valueOf(0)) > 0) {
if (ans.get(i).equals(BigInteger.valueOf(1))) {
if (i == 0) {
anss.append(ans.get(i)); } else if (i == 1) {
anss.append("x"); } else if (i == 2) {
anss.append("x*x"); } else if (i >= 3) {
anss.append("x**").append(i); }
} else {
anss.append(ans.get(i));
if (i == 1) {
anss.append("*x"); } else if (i == 2) {
anss.append("*x*x"); } else if (i >= 3) {
anss.append("*x**").append(i); } }
ans.remove(i);
break; } }
//
for (Integer i : ans.keySet()) {
if (!ans.get(i).equals(BigInteger.valueOf(0))) {
if (i == 0) {
anss.append("+").append(ans.get(i));
} else if (i == 1) {
if (ans.get(i).equals(BigInteger.valueOf(1))) {
anss.append("+x");
} else if (ans.get(i).equals(BigInteger.valueOf(-1))) {
anss.append("-x");
} else {
anss.append("+").append(ans.get(i)).append("*x");
}
} else if (i == 2) {
if (ans.get(i).equals(BigInteger.valueOf(1))) {
anss.append("+x*x");
} else if (ans.get(i).equals(BigInteger.valueOf(-1))) {
anss.append("-x*x");
} else {
anss.append("+").append(ans.get(i)).append("*x*x");
}
} else {
if (ans.get(i).equals(BigInteger.valueOf(1))) {
anss.append("+x**").append(i);
} else if (ans.get(i).equals(BigInteger.valueOf(-1))) {
anss.append("-x**").append(i);
} else {
anss.append("+").append(ans.get(i)).append("*x**").append(i);
}
}
}
}
if (anss.length() == 0) {
System.out.print(0);
} else {
if (anss.charAt(0) == '+') {
anss.delete(0, 1);
}
String ansss = String.valueOf(anss);
ansss = ansss.replaceAll("\\x2B-", "-");
System.out.print(ansss);
}
}
不难发现,这个方法有着较为庞大的if-else分支语句嵌套的结构,导致独立路径的条数多,判定结构的复杂程度就高;同时程序非结构化程度也相当高,通俗来讲就是不够”面向对象“,而过于“面向过程”,多个原因叠加导致这个方法模块认知复杂度较高。尽管我的代码没有检测出bug,但根据hank其他同学的经验来看,这样的部分的确是我们的“重点关注对象”,是bug出现的重灾区。
对于改进办法,我认为可以将其拆分为两个方法,一个用来实现term内的输出,另一个用来实现不同term之间的连接输出。笔者在第二三次作业中就采用了这种方法,从而有效降低了这个类的复杂度。当然在我看,为了更好的优化输出结构获得更好的性能分数,在代码静态分析的合理性上做出一定的牺牲也是具有合理性的。
测试思路与bug分析
本次作业在强侧与互测中均未发现bug,同时化简较为彻底,在强侧中获得了100分。
对自身程序的测试,首先进行模块化测试,针对不同模块的特定功能构造针对性样例测试。然后进行整体测试,主要是使用连续的正负号,以及幂函数,表达式因子的不同构造,从而实现对代码整体正确性的检测。
对于互测除上述方法之外,还应该针对该份代码的化简逻辑进行阅读与理解,找到其中可能存在的逻辑漏洞,然后构造针对性样例进行hank。
第二次作业
需求分析
第二次作业需要在第一次作业的基础上,完成对自定义函数、求和函数与三角函数的多项式的化简,最终输出恒等变形展开所有括号后的表达式。
本茨作业依然沿用了递归下降的解析方法,同时增加了三角函数因子类,此时再考虑到合并同类项的需求,之前的数据结构已经无法满足需求,最终经过考量采用了 HashMap<HashMap<String, Integer>, BigInteger> 的嵌套HashMap结构来存储数据,三个参数依次代表了因子的字符串内容,因子的次数,因子所处项的系数。
架构方案设计
由于本次新增的函数限制较多,形式比较单一,因此为了方便我采用了在预处理阶段检测出自定义函数和求和函数,然后直接调用处理方法返回替换后、能够符合解析要求的表达式,替换掉原先的字符串。最后对预处理完成之后的表达式进行解析和计算化简。
本次作业的UML类图如下所示:
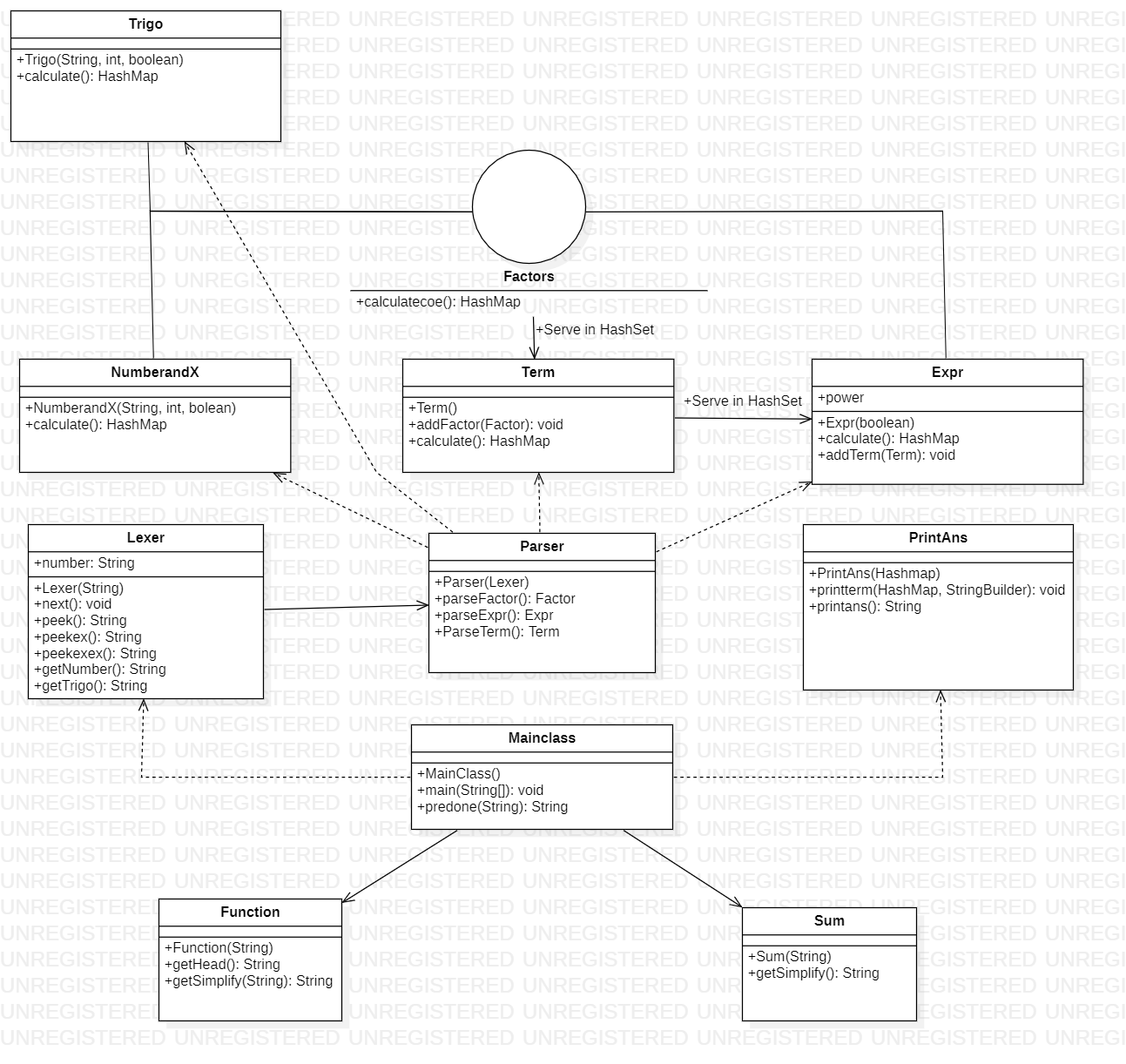
其实这样的架构并不够好,对Function、Sum两个类的可拓展性较差,当有更复杂的需求出现时(第三次作业),这样的架构显然就不够合适了。
代码结构分析
静态分析的结果如下:


通过观察笔者发现,出去calculate()这个方法的相对高复杂可以预见之外,我们主类的入口函数复杂度也相当高;经过阅读代码我发现,核心的原因是我进行了较为复杂的预处理,即相对第一次新增加的检测函数,调用方法并完成替换的过程,这一部分代码段结构较为复杂,也比较的面向过程,因此导致整个复杂度大大提升。
导致这一问题的本质原因其实就是不够合理的架构选择,当我在完成作业之后,看着主类里又长又臭的大段代码,也很难不意识到这个问题。因此我在下一次的作业中果断优化了架构,进而解决了这个问题。
输出优化策略
- x ** 2 --> x * x
- 当存在系数为正的项时,任选其一放在第一个输出
- sin(0) --> 0 cos(0) --> 1
- sin(-number) --> -sin(number) cos(-number) --> cos(number)
对于其他一系列三角函数公式化简策略,笔者认真思考了其实现的可能性,最终没有采用。一是因为实现的复杂性,要想覆盖一个三角公式的所有情形是较为困难的,也许我们能轻易实现sin(x)2+cos(x)2 = 1,但诸如3xsin(x)2+2*x*cos(x)2乃至更复杂的形式则不容易完全实现;二是因为投入产出比低,有效使用概率太低,而且极有可能因小失大,导致了正确性上的谬误。
本次作业最终强测拿到了95.1157分,个人感觉较为满意。
测试思路与bug分析
本次作业的架构尽管不够理想,但顺利通过了强侧,在互测中被 sin(0)^0 这一数据hank了一次,个人认为这是数学中的未定义行为,不应当作为合法数据,当然之前的指导书中似乎也有0^0==1的特殊规定,因此也算是一个小失误吧。
在互测中我也成功hank他人2次,本次作业中我认为关于三角函数的化简是极易考虑不周而出错的,尤其是第四条化简策略中三角因子次数为偶数时,许多同学任然保留的负号而导致错误。同时我也发现,采用预解析模式的同学,或是几乎没有优化化简的同学,反而不容易出现bug,hank难度较高,可能这也未尝不是一种好的策略。
第三次作业
需求分析
第三次作业中需要完成的任务为:读入一系列自定义函数的定义以及一个包含幂函数、三角函数、自定义函数调用以及求和函数的表达式,输出恒等变形展开所有括号后的表达式,同时本次没有了嵌套括号的限制。
架构方案设计
由于第二次作业的架构缺陷,我果断进行了架构的修改,,将Function类和Sum类也实现了Factor接口,,让其成为与表达式因子类似的可再分解的因子,最终表达式树的叶子节点依然全部为常数/x因子或三角函数因子。
本次作业的UML类图如下所示:
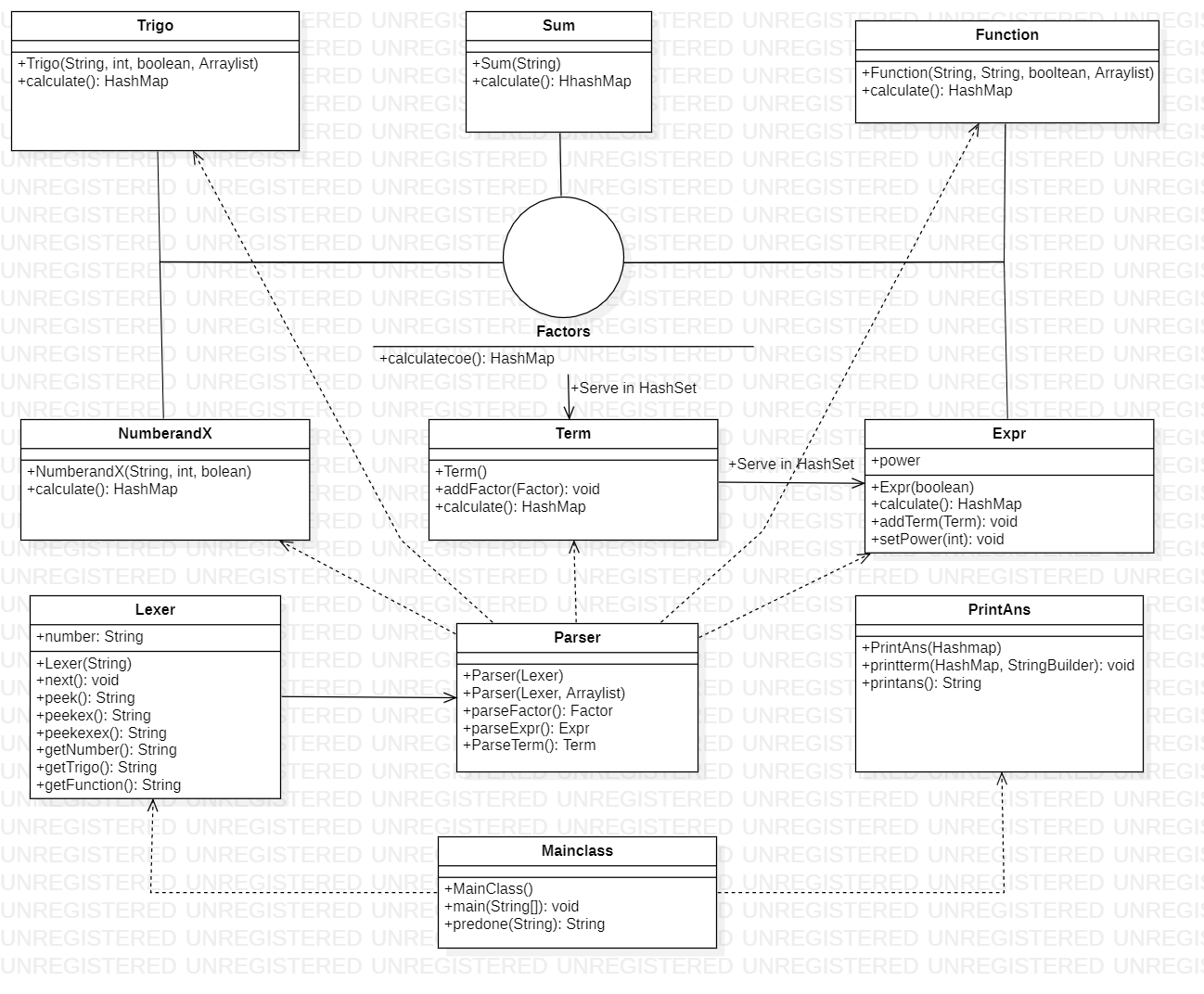
可以明显看出,本次作业的架构比第二次好了许多,UML图的层次也更加清晰,更加美观。
代码结构分析
静态分析的结果如下:
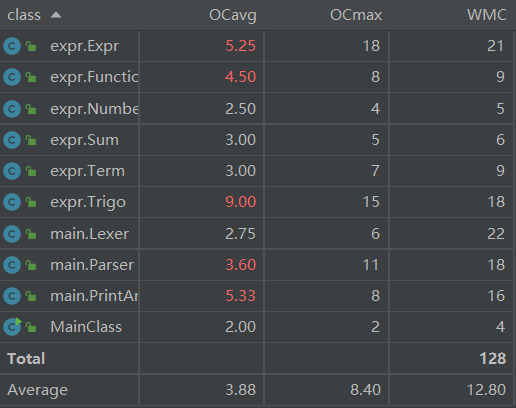

与第二次结果较为相似,整个复杂度也没有明显提升,故不再赘述。
测试思路与bug分析
本次测试依然是采用模块化测试+整体测试的模式来进行。注意简单样例对新增功能的重分测试,同时亦可将前两次强侧的数据拿来再次测试,以保证我们在增量开发的过程中未导致原有功能产生bug。
尽管本次作业的架构我个人感觉比较满意,但却犯了一些致命的错误。首先是有一段代码本应当注释掉我却忘记注释了,导致在互测中被多次触发导致bug。同时,由于我在for循环的循环条件和循环中调用.calculate()方法(正确的做法应当是先在循环开始前将.calculate()的结果存入一个新的变量中,在for循环中使用该变量而不是频繁调用.calculate() ),导致我的时间复杂度成指数增长,在强测中有三个测试点因此而TLE。
当然本次互测我也成功hank他人12次,主要的检测点为sum函数上下界的数据范围,测出了不少没有用BigInteger存储的同学,同时还有一些同学对三角函数内表达式化简的处理存在明显的逻辑漏洞,对于非因子的结果未加上必要的括号。
反思与反省
本来可以以一个比较完美的结果结束第一单元,我却因为疏忽大意和不良的代码习惯而导致了不少丢分,如果我做了更充分的自我测试,一定能够在提交之前发现那段没有注释掉的代码,如果我能在开发过程中及时想起老师不止一次关于不良代码习惯大力批判,也许就能避免TLE。看着寥寥几行的修改就能够完成所有这些bug的修复,我更加懊悔。不过事后平静下来仔细想想,许多东西的确都是在付出了相当的代价之后才能深入人心。权当是对自己不够成熟的一次惩罚吧。
心得体会
第一单元的OO之旅已经结束了,尽管从结果上看有不小的遗憾,但是从学习过程与收获的角度上来看,至少我认为是十分丰富的。这是第一次面向对象设计与构造课程第一单元的作业,也是我第一次接触JAVA,第一次系统学习面向对象的编程思想(JYP老师则认为不应该将面向对象局限成一种编程思想,它应当是一种认识世界的思想)。这三周以来,每周五的晚上到周六的凌晨,我总能在自习室遇到几个熟悉的小伙伴,似乎已经形成了一种心照不宣的默契。从第一次作业的整整两天翻阅资料无从下手,到后来能够理清相对清晰的架构再相对有条不紊的进行代码编写,我不仅有了代码水平上的提升,更重要的是克服了内心的障碍,让我对一些看似难于下手的新东西有了尝试的勇气与自信,这份勇气与自信也是我面对今后更大挑战的底气。
希望接下来的OO之旅更加精彩,也更加顺利。



