基于吴恩达的深度学习
实验顺序(根据对应的README.md)
Supervised Machine Learning: Regression and Classification
week1
- Overview of Machine Learning:加入社区和课程相关内容,可忽略
- Supervised vs. UnsupervisedMachine Learning:了解python,jupyter和markdown
- Practice Quiz Supervised vs unsupervised learning:区分监督学习与无监督学习的类型
- Regression model
- 线性回归的模型表示:构建了两个样例的线性回归,并且用matploit进行绘制
- 成本函数
- Practice Quiz Regression Model:梯度下降的实习,具体包括代价函数公式,代价函数求导公式,梯度下降公式的实现,学习率的设置
- Train the model with gradient descent:简单测试
- Practice quiz Train the model with gradient descent
week2
C1_W2_Lab01_Python_Numpy_Vectorization_Soln
C1_W2_Lab02_Multiple_Variable_Soln
C1_W2_Lab03_Feature_Scaling_and_Learning_Rate_Soln:主要说明了z-score normalization的使用,如何训练模型,如何使用训练后的模型以及对学习率,参数值大小的影响
C1_W2_Lab04_FeatEng_PolyReg_Soln:scikit-learn使用
sklearn.linear_model.SGDRegressor:梯度下降回归模型[sklearn.preprocessing.StandardScaler:z-score标准化week3
C1_W3_Lab01_Classification_Soln:最后一个Cell的按钮似乎有些问题
C1_W3_Lab02_Sigmoid_function_Soln:了解sigmoid function,以及样本点对阈值对应的z值的影响
C1_W3_Lab03_Decision_Boundary_Soln:阈值与决策边界的区别与联系
C1_W3_Lab04_LogisticLoss_Soln
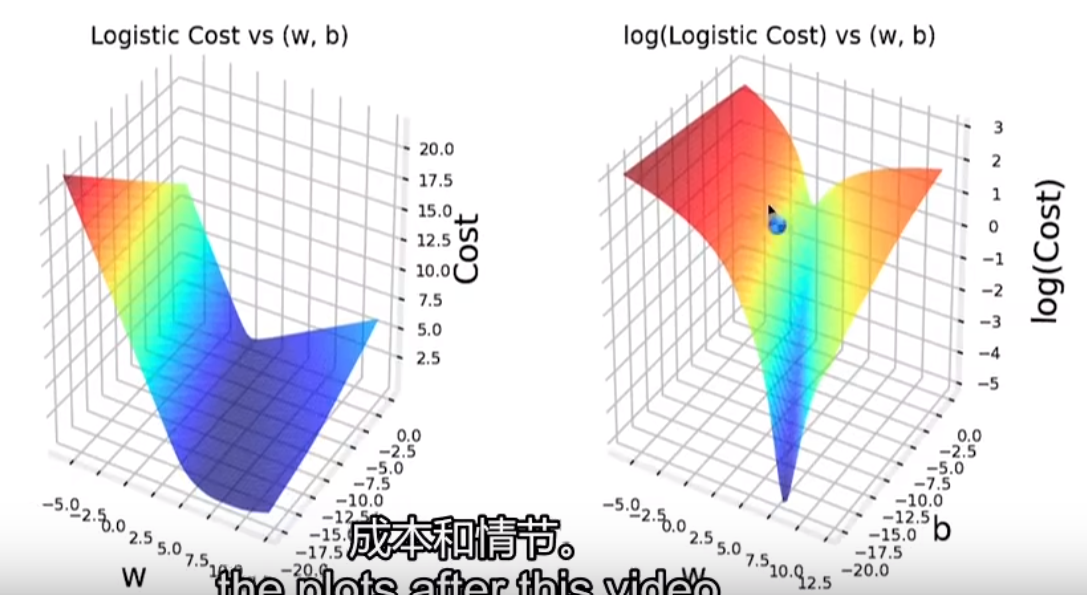
- 平方误差成本函数不适用于逻辑回归,因为不够平滑
- 逻辑成本函数的特点
C1_W3_Lab05_Cost_Function_Soln:逻辑回归中的成本函数
C1_W3_Lab06_Gradient_Descent_Soln:逻辑回归中的梯度下降
C1_W3_Lab07_Scikit_Learn_Soln:使用scikit-learn训练模型,并通过
print("Accuracy on training set:", lr_model.score(X, y))验证准确度,其中X是训练数据的特征,y是训练数据的目标值C1_W3_Lab08_Overfitting_Soln:过拟合样例,实际上无法使用
C1_W3_Lab09_Regularization_Soln:正则化改变了成本函数的计算公式,进而改变了梯度下降的计算公式。图表无法点击
C1_W3_Logistic_Regression
sigmoid函数
成本函数
梯度下降函数
预测
注:文档给出的准确率是92,但我这里最终只有91
特征工程(属于week2的内容)
正规化
Advanced Learning Algorithms
week1
C2_W1_Lab01_Neurons_and_Layers:
构建线性回归模型
查看tensorflow中训练好的参数(weights,bias):
linear_layer.get_weights()构建逻辑回归模型
C2_W1_Lab02_CoffeeRoasting_TF:
对训练数据的归一化(单独的一层)
get_weights获得的矩阵:w1[0]代表第一个神经元需要的参数[-0.72 1. 0.1 ]问题:关于咖啡豆烘焙的例子,为什么第一个隐藏层定义了三个神经元(
w1.shape(1)),而且这三个神经元使用的都同样是输入层的两个特征,这似乎没有意义啊?C2_W1_Lab03_CoffeeRoasting_Numpy:用numpy实现神经网络
C2_W1_Assignment:通过神经网络实现识别图像中的0/1
print(f"model.input.shape.as_list():{model.input}")调用错误:似乎需要模型初始化后才能调用,建议后面的代码运行完后再回过头来尝试- 使用矩阵实现所有计算
week2
week3
C2_W3_Assignment:若给的分类
y=[1, 2, 0],yhat=[1, 2, 3],则的计算方式为Unsupervised Learning: Recommenders, Reinforcement Learning
week1
C3_W1_KMeans_Assignment:使用k-means进行图片压缩
原图像
128*128*24(长*宽*像素)注:rgb每个8位
压缩后的图像
128*128*4压缩原理:使用k-means算法,选取最高频的16个像素点,代替所有像素点
C3_W1_Anomaly_Detection:异常检测,且使用了精度,召回率,分数选择最佳的参数
week2
C3_W2_Collaborative_RecSys_Assignment:协同过滤,数据集包含用户对电影的评分,向量w,x维度由自己定义
C3_W2_RecSysNN_Assignment:基于内容的过滤,数据集包含用户对电影的评分,电影的特征向量,用户的特征向量等
注:基于内容的过滤最后需要将两个神经网络的输出向量做点乘,但似乎向量之间的元素看上去是没有对应关系。注意到整个神经网络的输出值是两者的点乘,进而通过成本函数和梯度下降使两者拟合
week3
- C3_W3_A1_Assignment:windows系统无法使用
Display(visible=0, size=(840, 480)).start();注:
- 课程每个部分的week数正好与实验统一
- 使用jupyter notebook 想要matplotlib交互,将%matplotlib widget改成%matplotlib notebook
1|0一、深度学习的基本概念
-
深度学习与机器学习的关系:深度学习是机器学习的一个子集,主要使用神经网络
-
通用人工智能(Artificial General Intelligence,AGI):使用机器学习使用
-
训练集(training set):用于训练模型的数据集,通常用表示训练集中第i行的训练数据,也称为特征
-
目标集(target set):与训练集相对的结果值,通常用y表示
-
成本函数(cost function)
-
分类:根据有无结果(监督)
-
监督学习
-
特点:有训练集,有目标集,进而可以构造函数
-
分类
-
回归(Regression):函数连续,一对一
常见的目标函数形式:
-
:特征值个数,
注:下表表示特征值
-
:特征值系数的个数,,其中n为最高项阶数
算法:
- 线性回归
- 决策树
- 随机森林
- 支持向量回归
- 神经网络
-
-
分类(classification):函数离散,多对一
算法:
- 决策树
- 随机森林
- 支持向量机
- 神经网络
应用:图像识别
-
-
-
无监督学习
- 特点:有训练集,也可能有目标集,但目标集不用于程序学习,而是供人参考来设置参数
- 分类
- 聚类(Clustering)
- 异常检测(Anomaly detection)
-
-
线性回归:通过线性函数拟合
-
特点:在机器学习中,我们提到的线性函数通常是指一次线性函数
-
步骤
- 输入训练集和目标集
- 构建线性函数f
- 输入待估测的数值x,得到对应的
-
构建拟合函数:
-
代价函数(cost function)
-
比较拟合函数和代价函数:变量不同,拟合函数以x为变量,代价函数以a,b为变量
-
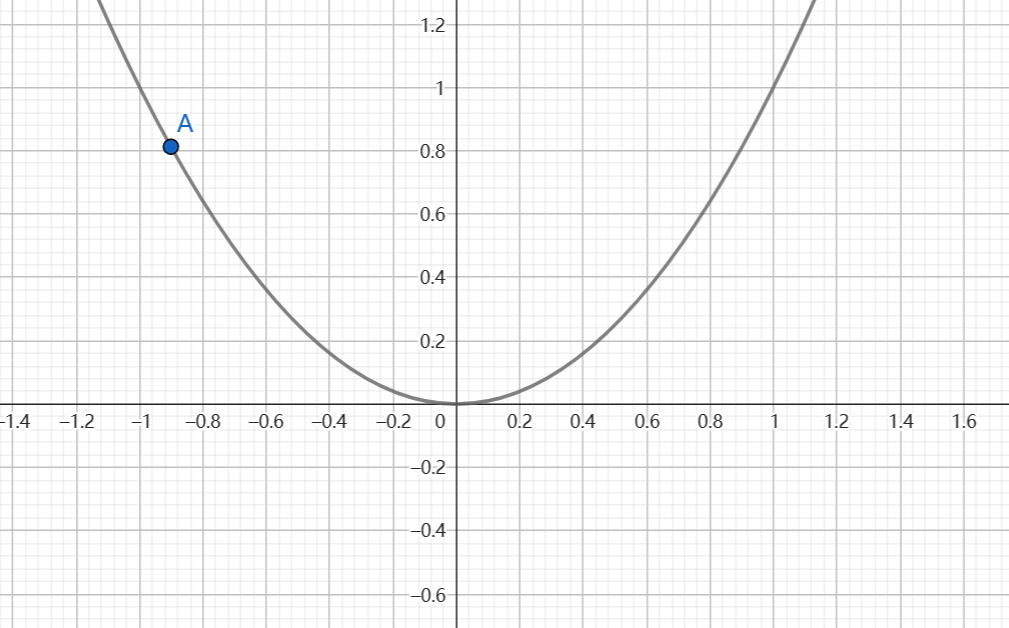
梯度下降:
-
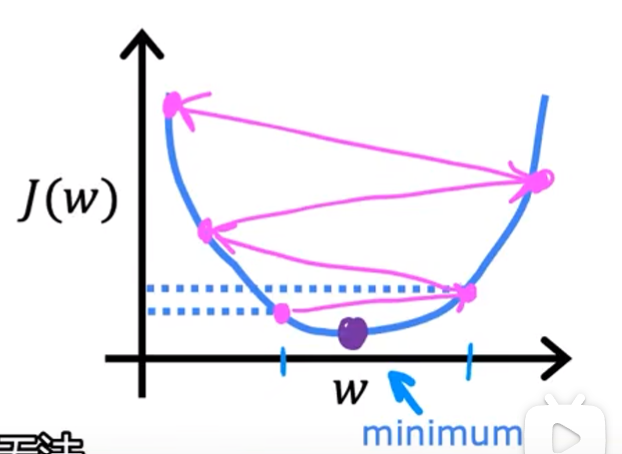
梯度下降原理,以线性函数为例,因为这是一种常见的极小值点情形
-
同时更新两个参数的梯度下降公式:
-
- :学习率
- :代价函数
注:对于有两个变量的函数,可以看做是一个三维图像,需要同时对两个变量做梯度下降处理
-
-
code
注:
-
计算
-
,且
注:
- 从数学的角度看,这个公式可以简化为
- 这里的求导运算是我们手动完成的
-
,且
-
-
赋值
-
注:这里梯度的实际上是一个向量,代指了下降最快的方向
-
-
-
线性拟合的基本流程
- 确定拟合函数
- 确定成本函数
- 最小化成本函数值,如通过梯度下降确定参数
- 确定起始点
- 确定梯度方向
- 确定学习率
2|0二、多元线性回归
-
多元线性回归
-
特点:有多个特征值
-
表达式:
-
拟合函数:
注:表示点击,
-
成本函数:
-
梯度下降函数:
-
-
-
正规方程(Normal Formula):非迭代的梯度下降算法,只适用于多元线性回归,且在特征值大于10000时会变得比较慢
注:该方法通常不需要机器学习的研究者实现,但应该知晓在机器学习相关的api调用的底层可能使用了该方法
-
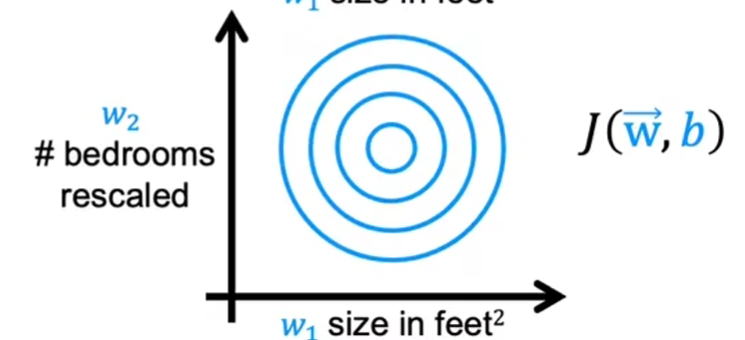
特征缩放(Feature Scaling)
-
作用:通过使各个特征的数量级一致,改善梯度下降的效果。具体来说,在特征的数量级过大时提高收敛速度,在特征的数量级过小时避免震荡
-
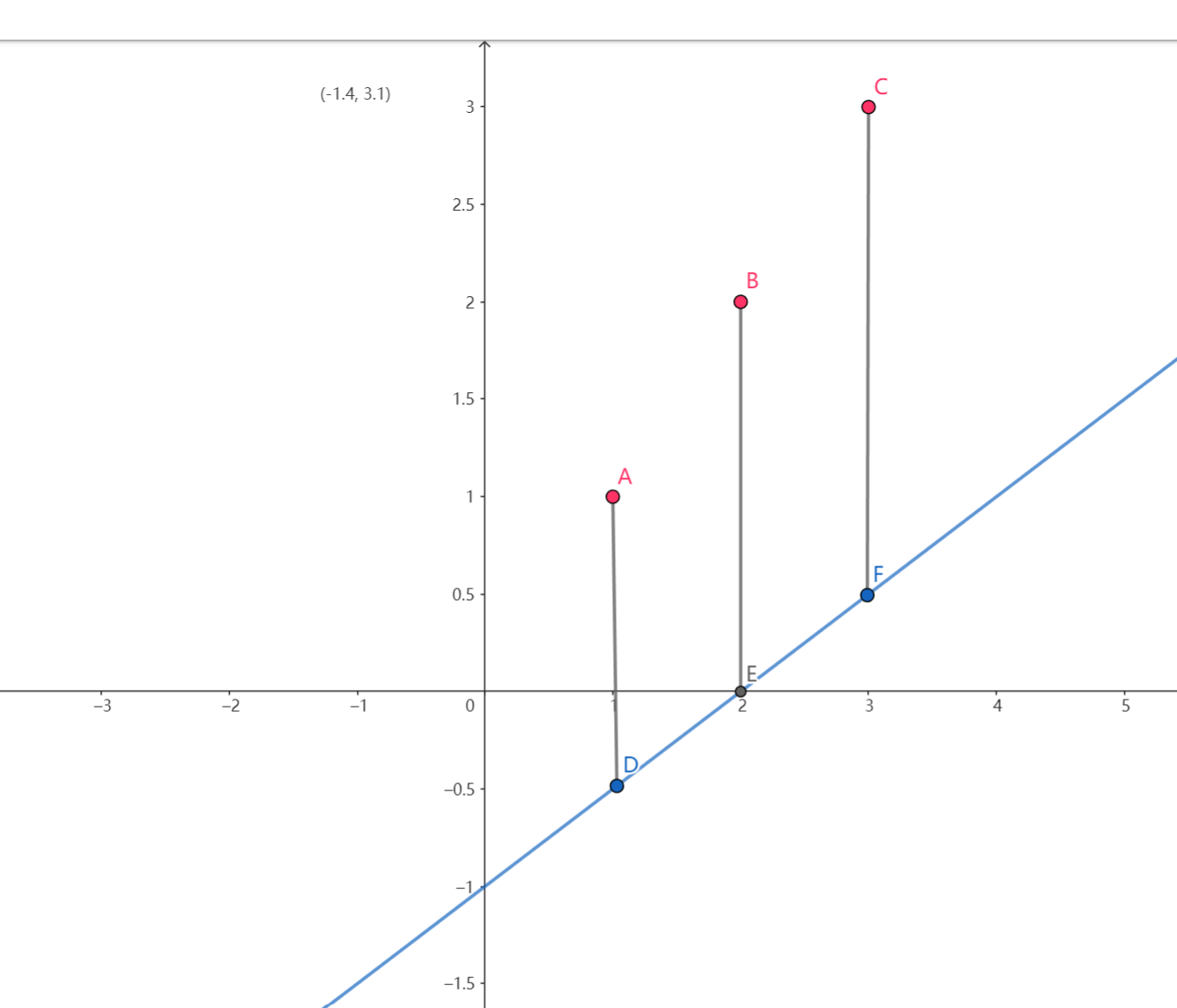
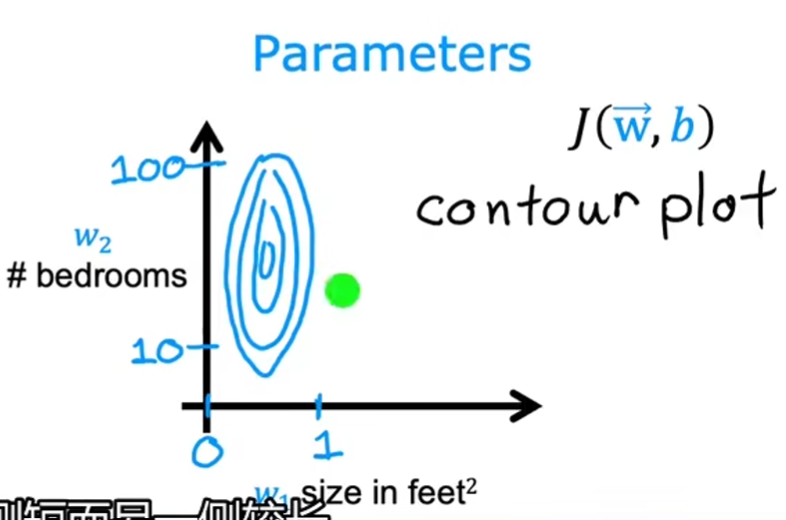
基本原理:不同的特征有不同的范围,以两个特征值的等高线图为例
-
实现的几种方式()
-
除以最大值的归一化
公式:
特点:最大值为1,最小值非0,故映射范围小于1,映射范围
-
均值归一化(Mean normalization)
公式:设为均值,择有
特点:使y轴两侧的样本点数一样多,同时使y的映射范围为
-
Z-score normalization
公式:设为标准差,则有
注:将看做是均值,看做,映射后分布接近于标准正态分布,超过的数据集中在之间
-
-
通过归一化后的参数进行模型预测:通常将学习率设置为
1.0e-1注:归一化后模型中的参数通常不会差一个数量级
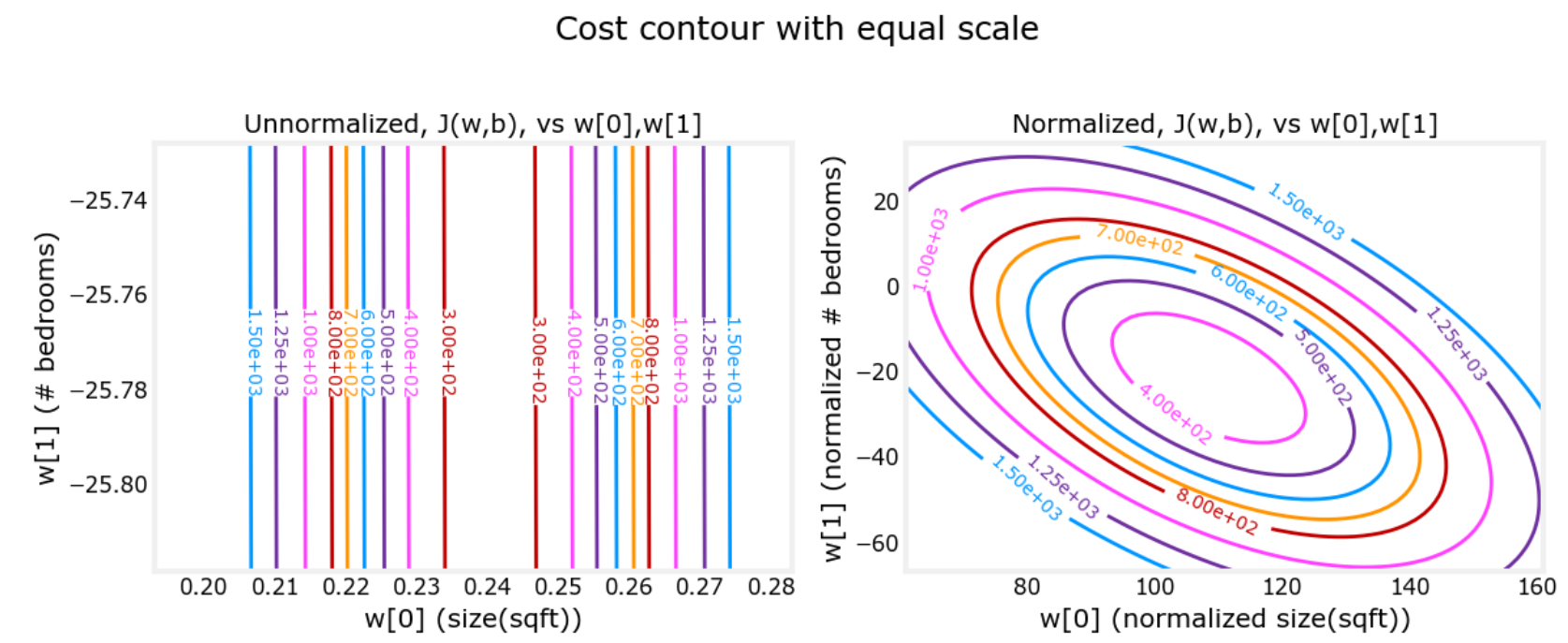
-
使用归一化的模型:当我们用一个归一化后的模型通过房子大小等特征预测房价时,需要将对应的房子大小等特征归一化处理后再输入,进而得到对应的房价
-
-
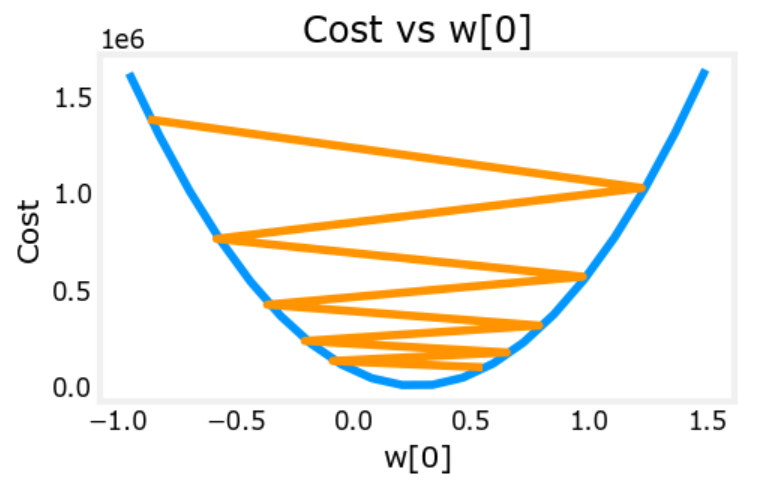
判断梯度下降是否有效
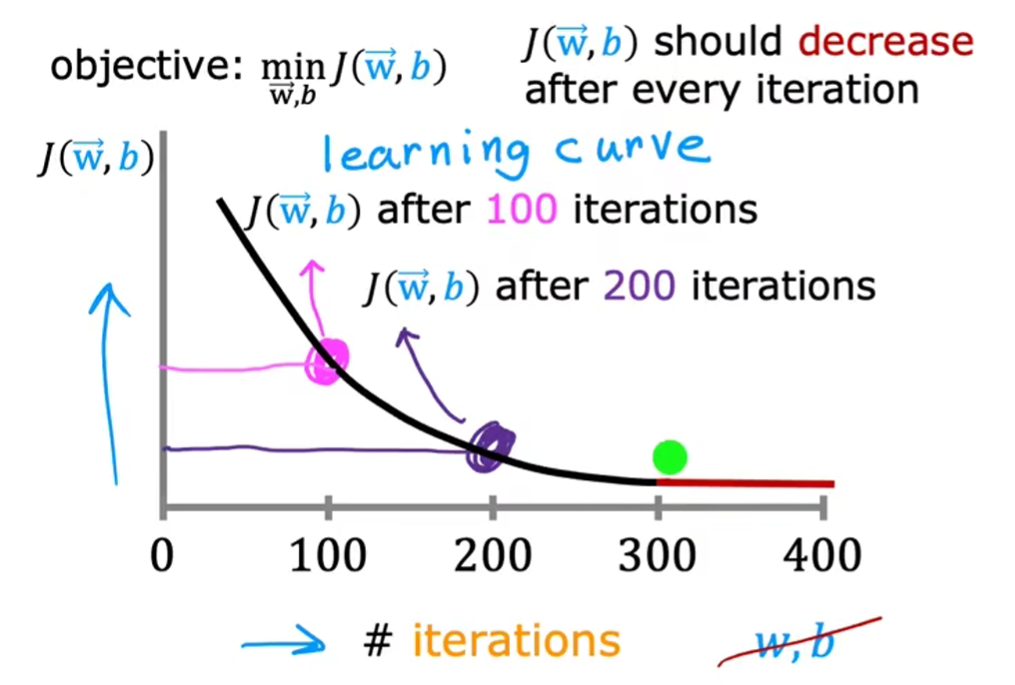
注:
- 横轴:迭代次数
- 纵轴:成本
如何看图
- 理想情况下,随着横轴的增长,纵轴总是减小的。如果变大,则说明学习率过大,从而出现了震荡
- 当迭代次数达到300次,函数以基本收敛
自动化的收敛判断:可以设收敛阈值为,如果随着迭代次数的增多,成本函数的下降值小于收敛阈值,则可以判定为收敛
注:实际上这里设置收敛阈值是极其苦难的
-
如何设置学习率:由小到大测试,如果遇到震荡就调小一点
-
特征工程:通过某种转换方式对应map_feature函数,将原始的特征空间映射到一个新的特征空间
优点:增加参数,参考例2,如果原本只有两个参数,转换后有27个参数,多项式拟合效果更好
缺点:可能导致过拟合
例:
-
对于一个房子有长和宽两个特征,则面积(长*宽)可以作为一个新的特征
-
某个将两个特征转换的map_feature函数
-
-
多项式回归(Polynominal Regression)
基本形式:
注:
- 表示第i个特征
- 每个特征值都是一个独立的多项式
3|0三、分类
-
分类介绍
-
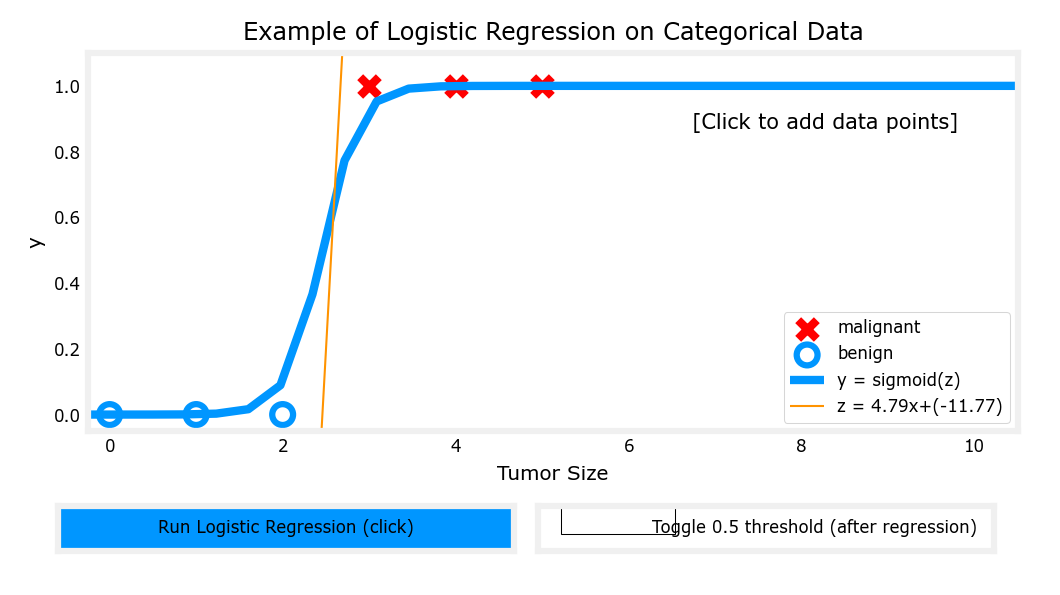
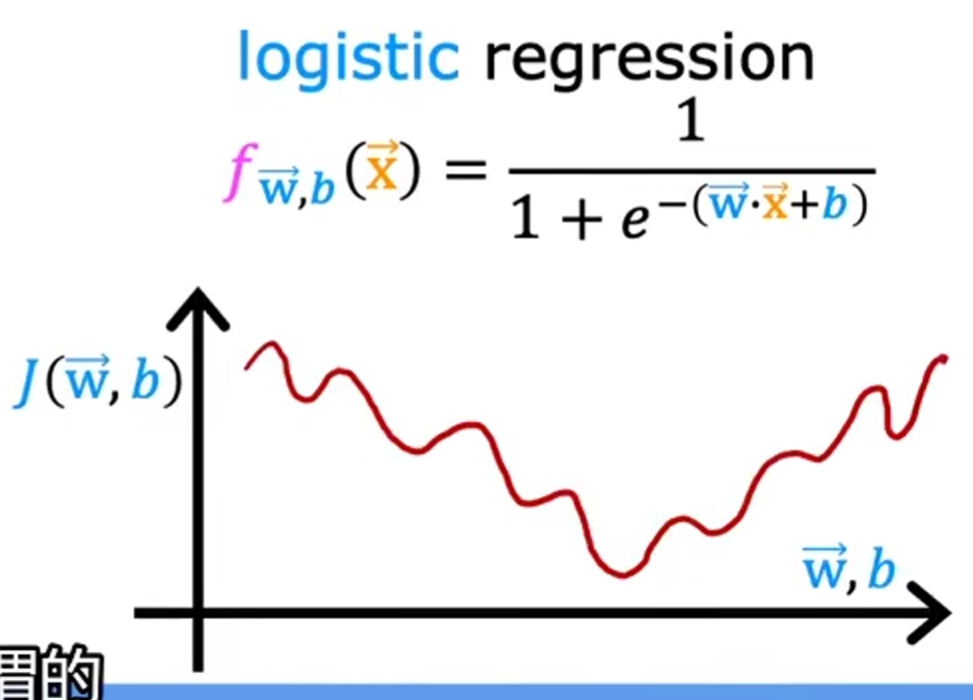
逻辑回归
激活函数(sigmoid function/logistic function):
注:
-
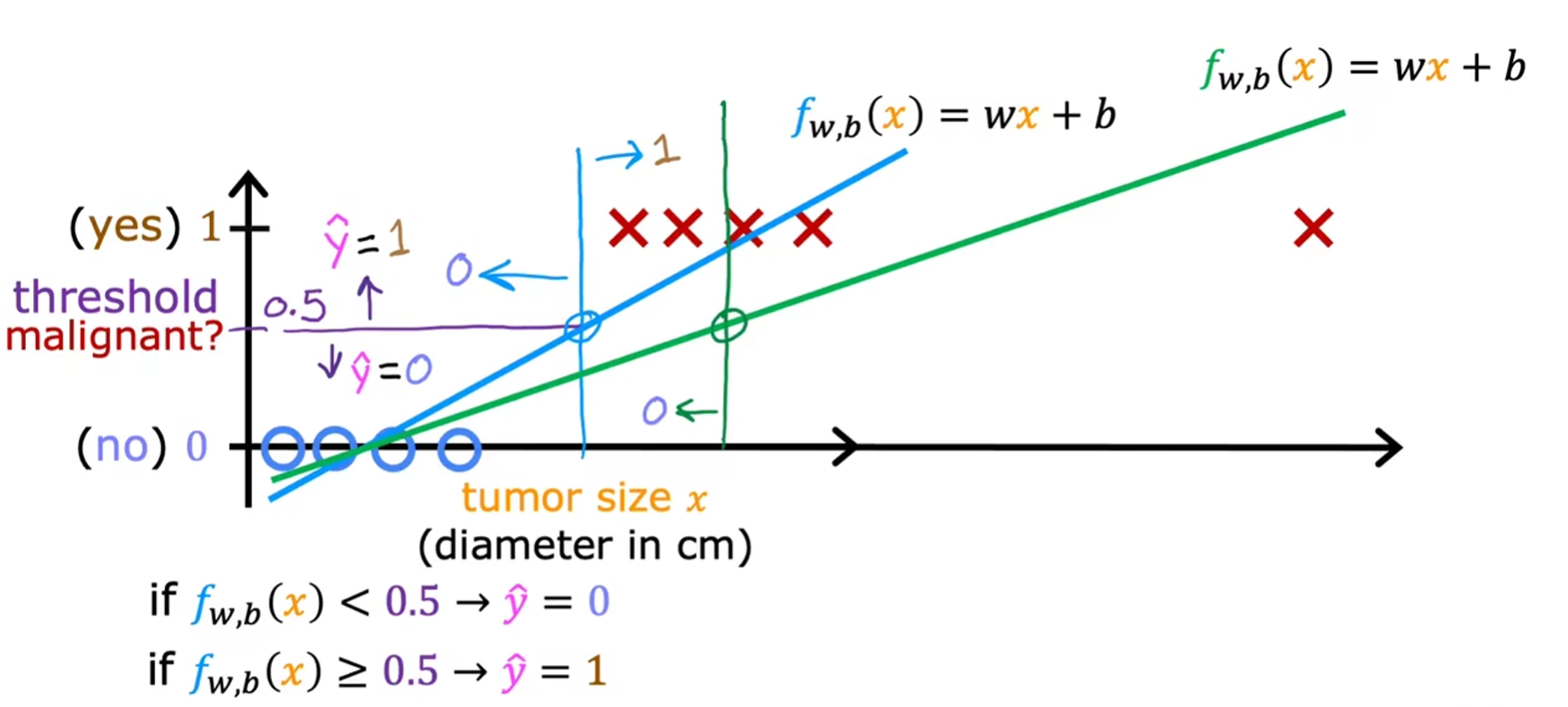
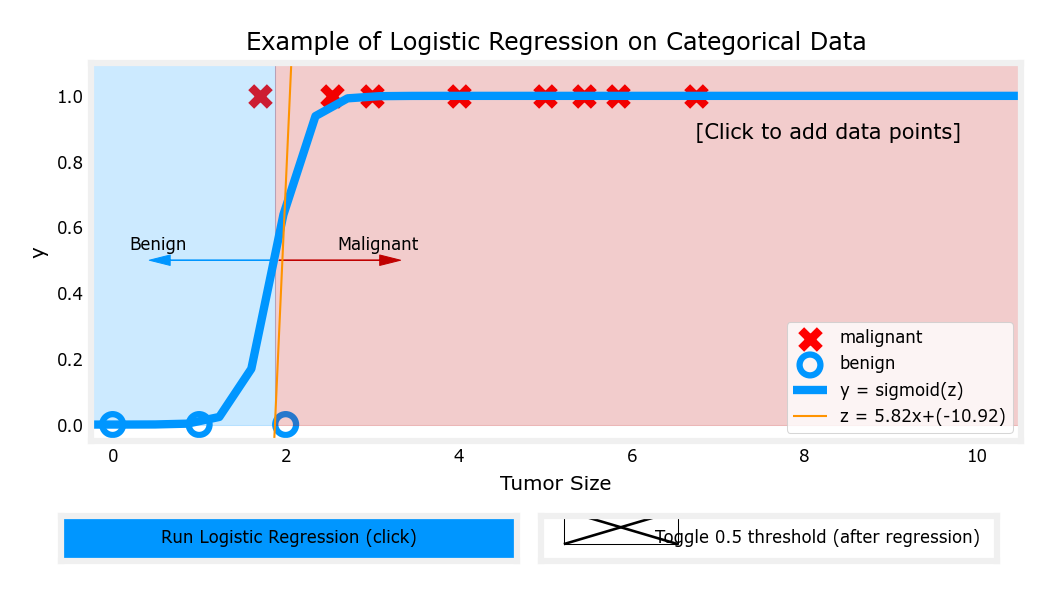
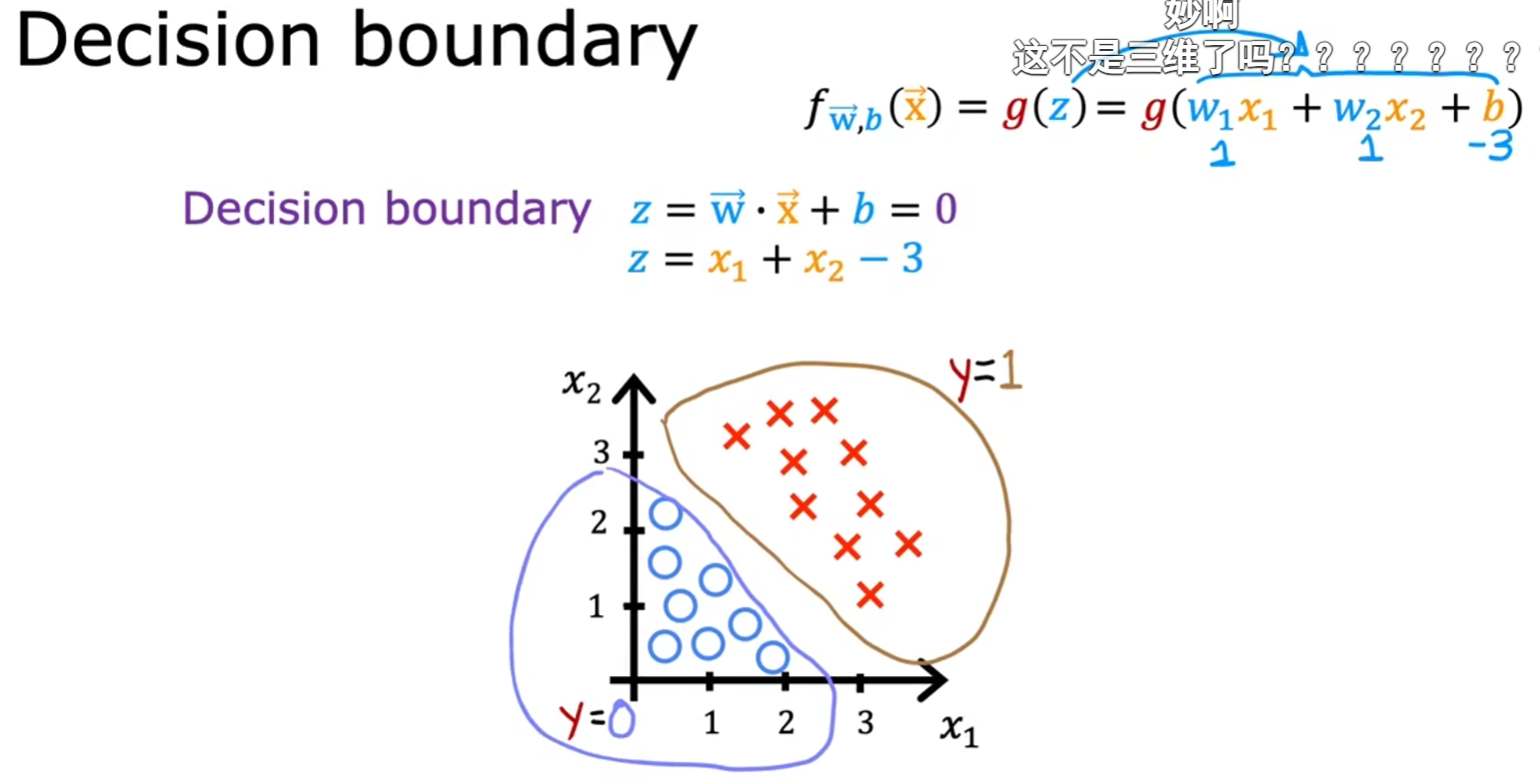
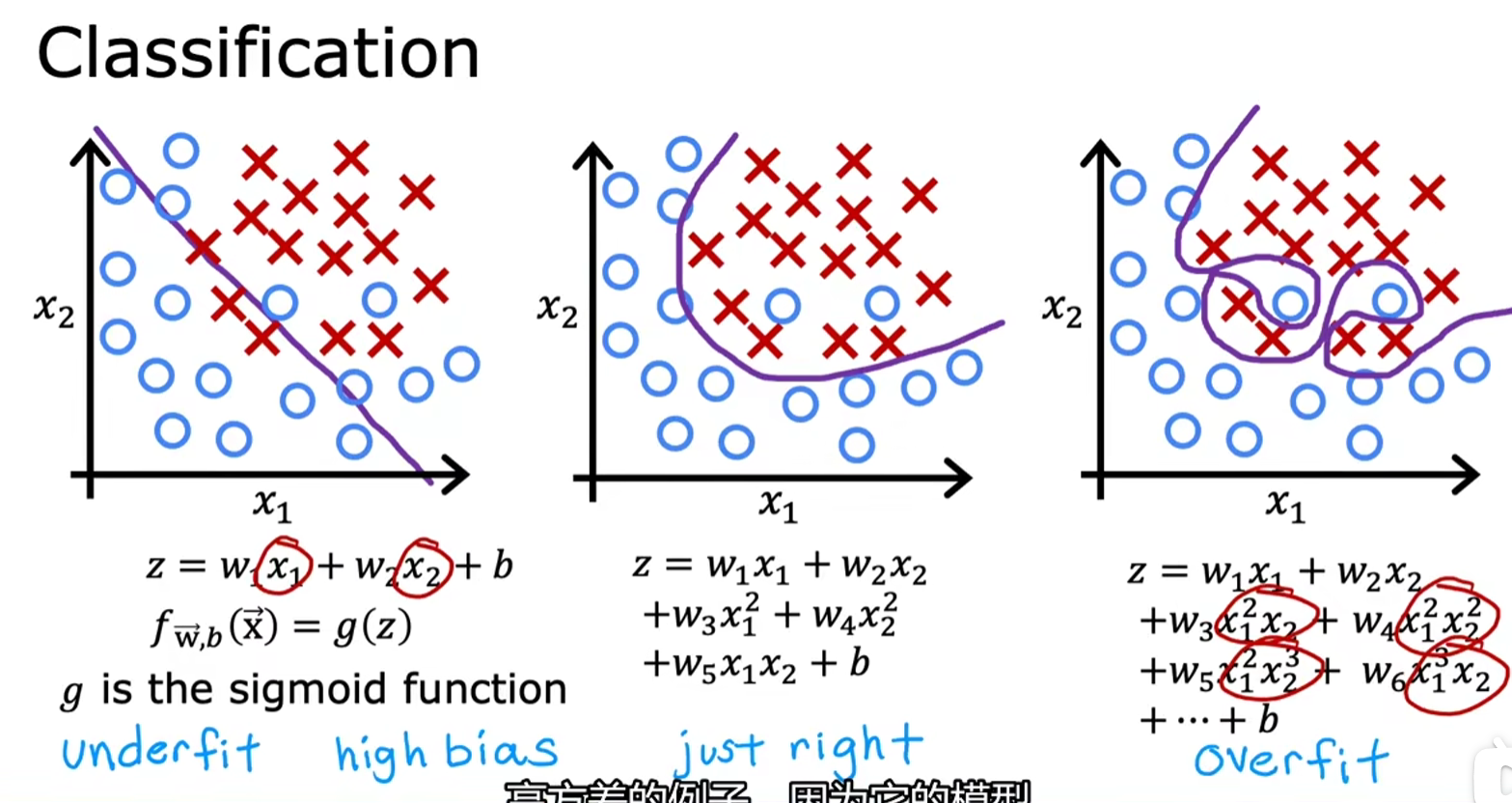
决策边界(decision boundary)
二维特征
- 由于圆圈代表的第三维z数值为0,叉叉代表的第三维z数值为1
- 不妨令z=0,即可解得圆圈的边界
-
逻辑回归中的成本函数
-
梯度下降
-
对成本函数求导:其中
注:这里w是系数(设是的系数),b是常数项
-
在计算时对所有参数做同步更新
-
code
-
-
过拟合(overfitting)问题
-
欠拟合与过拟合
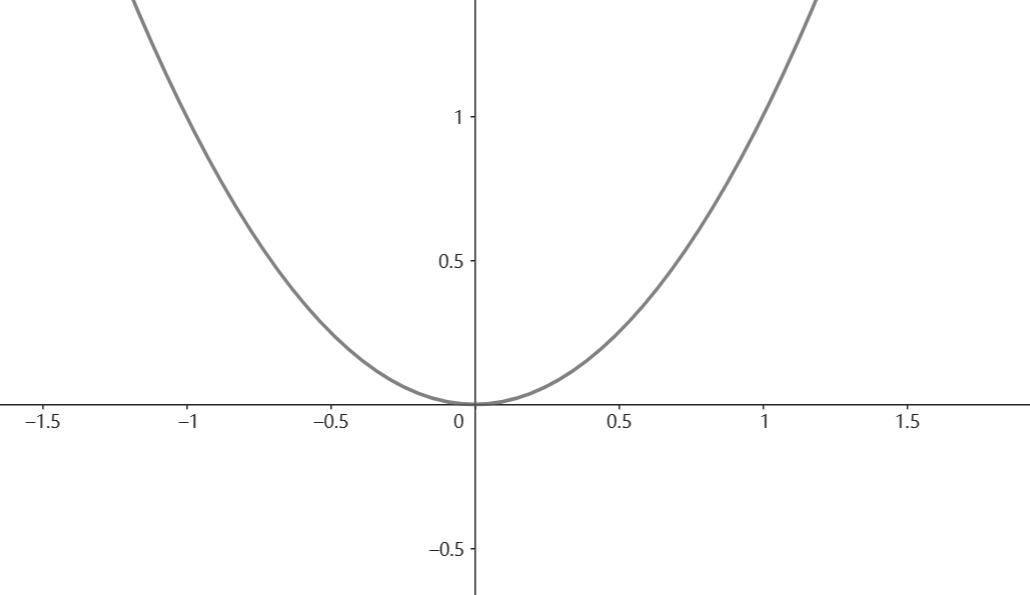
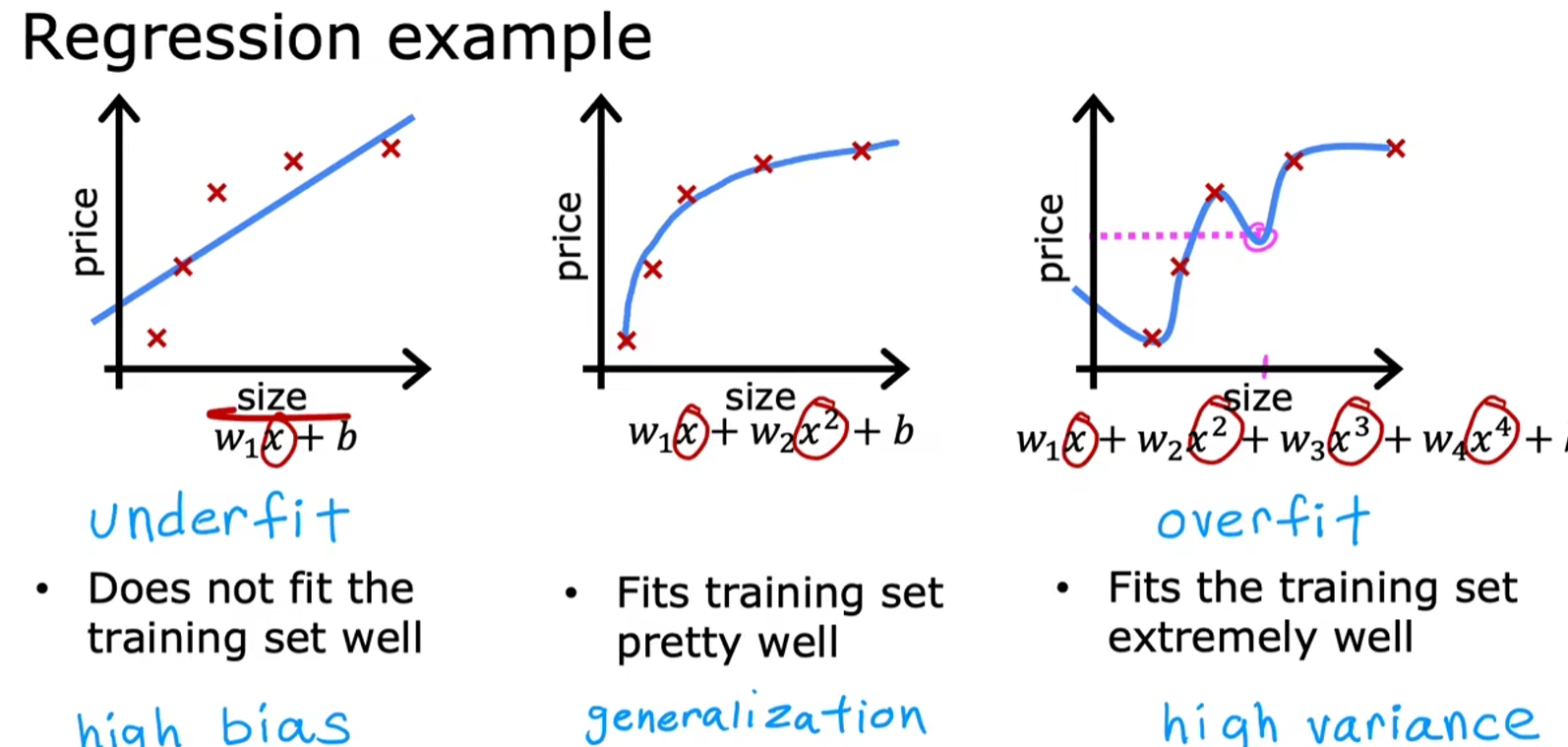
- 欠拟合:最高项的阶数较低,回归函数与样本偏差较大(对应图1)
- 过拟合:由于满足样例的回归函数可能有多种,当最高项的阶数较高,因为通常这种情况下曲线会变得不那么平滑,因而不适用于新的样例。如图中,第三个样本点与第四个样本点之间的拟合数据,显然这与我们生活认知中的面积越大,房价越高相出入,无法进行很好地泛化(generalization)
-
泛化:从下面更进一步的例子看,第三种拟合方式确实更贴近数据集,但由于过渡不够平滑,无法很好地进行泛化,因此更倾向于使用第二种阶位更低的拟合方式
-
处理
-
收集更多的数据:数据越多,拟合得越准确
-
特征选择(feature election):特征之间的相关性越好,拟合效果也越好。因为通过忽略无关或冗余的特征可以减少模型的复杂度,从而防止过拟合。
-
正则化:缩小高阶特征数据的系数影响,即使系数越小越好,最好为0避免出现过拟合的现象
注:通常不修改常系数
-
-
-
正则化(regularization)
注:正则化只影响参数w,不影响参数b
-
使用正则化后的成本函数:
- :误差
- (regu):正则项
- :正则化参数
注:
- 对于线性回归和逻辑回归,正则项相同
- 成本函数优化的目标不变,仍然是越小越好
-
对正则化后的成本函数求导
-
正则化参数的影响
- 当正则化参数较小:即取0,成本函数退化为初始版本,容易出现过拟合的情况
- 当正则化参数较大:显然,的权值会整体较大,为了使保持较小,在极端情况下应该让,故此时有目标函数退化为平行于x轴的直线,即欠拟合
- 综上:对于正则化参数的选取,可以参考学习率过大或过小都不好。
-
正则化的两种方式
-
code
-
正则化之后的成本函数表示
-
正则化之后的梯度下降表示
-
-
4|0四、神经网络(深度学习)的基本概念
-
基本概念
-
相关领域:语音识别,计算机视觉(cv),自然语言处理(nlp)
-
使用实例
-
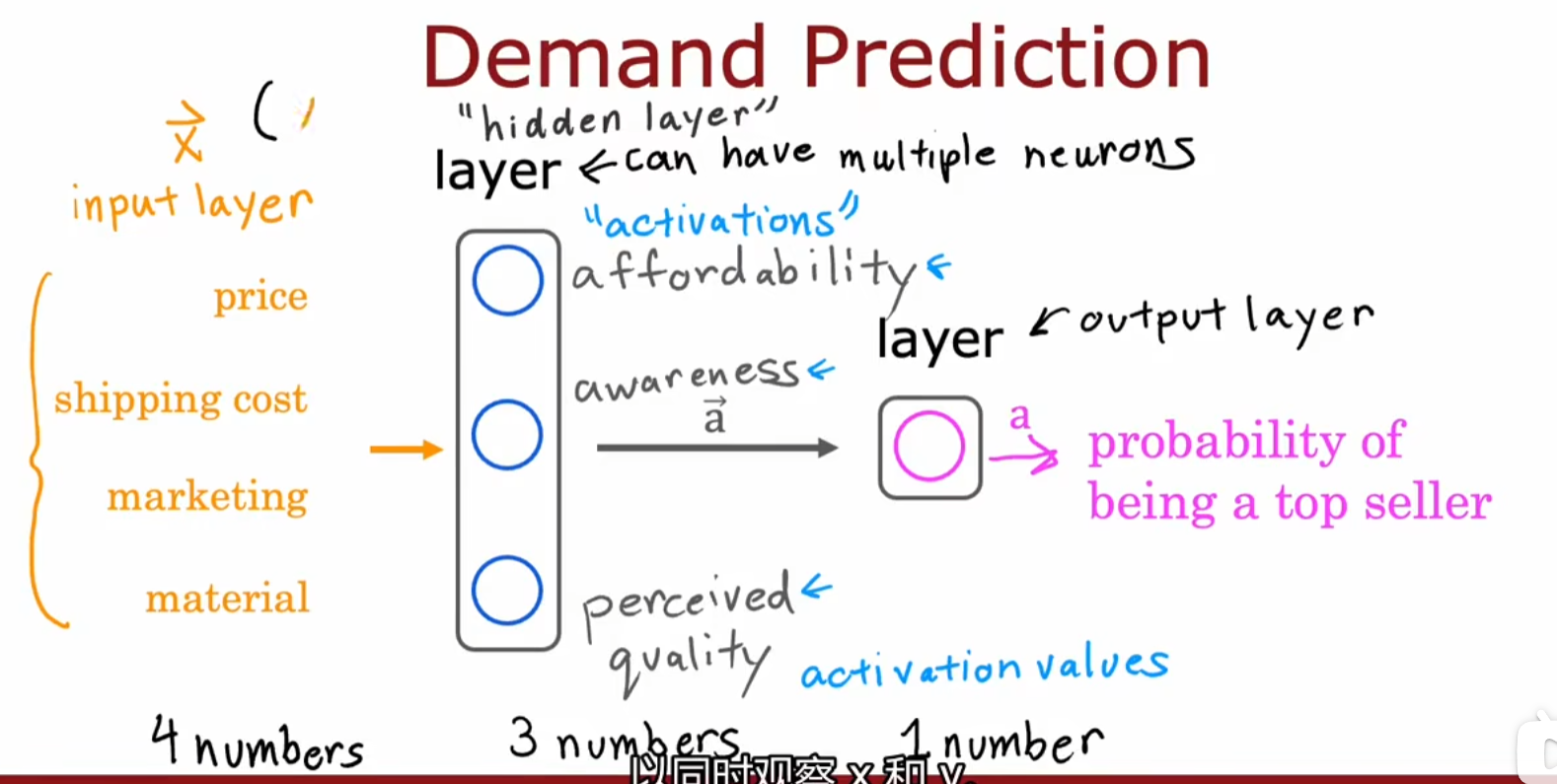
基本数据层(input layer):price,shipping cost,marketing,material
-
隐藏层/多层感知器(hidden layer/multilayer perceptron):分为独立的affordability(对应price,shipping cost数据),awareness(对应marketing数据),perceived quality(对应price,material数据)三个神经元,每个神经元所对应的函数都是linearner regression,logistics regression等。
输出:activation values
注:隐藏层的层数和每层的神经元个数才是重点
-
输出层(output layer):将上一层的输入作为输出,从而预测top seller的概率
-
-
图像感知举例(cv)
-
-
如何构建一层神经网络
-
第i层的表达式:
- :表示第几层,输入是第层的数据
- :表示第几个单元,对于第0层来说就是输入的特征数
- :表示第l层的第j个单元输出结果,是一个标量
-
前向传播算法(forward propagation)
注:
- 通常越靠近Output,每层的单元数越少
- 训练模型用的是反向传播,计算时用的是前向传播
-
-
tensorflow使用
-
定义数据集
注:每一行包含所有的特征
-
tensorflow与numpy中matrix的转换
-
构建模型:确定神经网络的层次,每层的神经元个数,激活函数
-
编译模型:确定损失函数,学习率
-
训练模型:通过数据获得参数w,b
-
模型预测
-
-
单个网络层上的前向传播
作用:获得前一个层的输入,求当前层的输出
常见的网络层:dense layer,卷积层(convolutional layer)
-
强人工智能
AI
- ANI(Artificial narrow intelligence):self-driving car,web search
- AGI(Artificial general intelligence)
-
高效神经网络
5|0五、神经网络训练
-
tensorflow训练
-
构建神经网络
-
确定成本函数
BinaryCrossentropy():对应分类中基于损失函数的成本函数 -
训练模型
-
-
激活函数
-
常见激活函数
-
linear function:
- 值域:
- 适用:明天股票相对今天股票变化,因为此时值域可以为正负
-
sigmoid:
-
值域:
-
适用:二分问题的输出层
-
-
Rectified Linear Unit(ReLU,整流线性单元):
值域:
注:与sigmoid比较可知,当,在sigmoid中,在ReLU中
-
-
激活函数选择
-
输出层:根据输出结果的值域选择激活函数
-
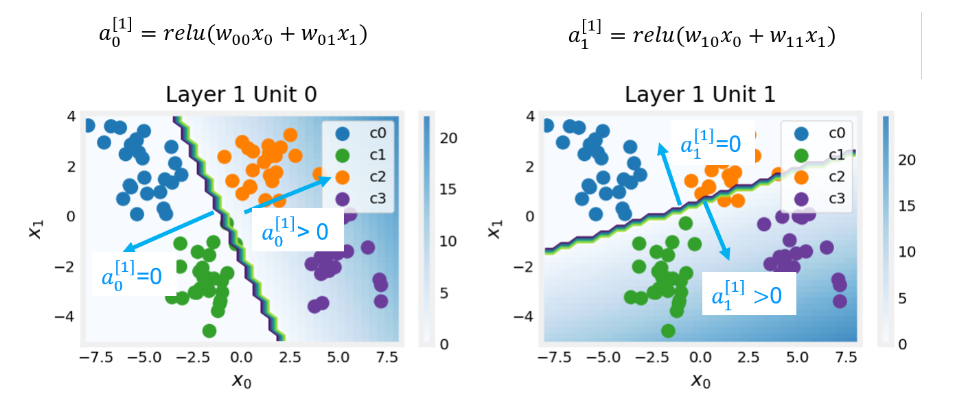
隐藏层
-
ReLU是最常见的选择,而不是sigmoid,原因如下:
-
ReLU计算简单,速度较快
-
观察ReLU和sigmoid的图像可知,ReLU一端平坦,sigmoid两端平坦,故前者对应的成本函数导数值较大,梯度下降快
注:目标函数和成本函数之间的关系是间接的
-
-
不建议在隐藏层中使用linear function
-
-
-
为什么需要使用多种多样的激活函数,而不是统一使用线性激活函数:重复使用线性激活函数,相当于只使用了一次线性激活函数
-
-
多分类问题
-
思想:将0/1问题泛化为0/1/2/3问题。若在前者的问题中,等于0的概率为a,则等于1的概率为1-a;进而在后者的问题中,等于0的概率仍为a,但等于2/3/4的概率为1-a
-
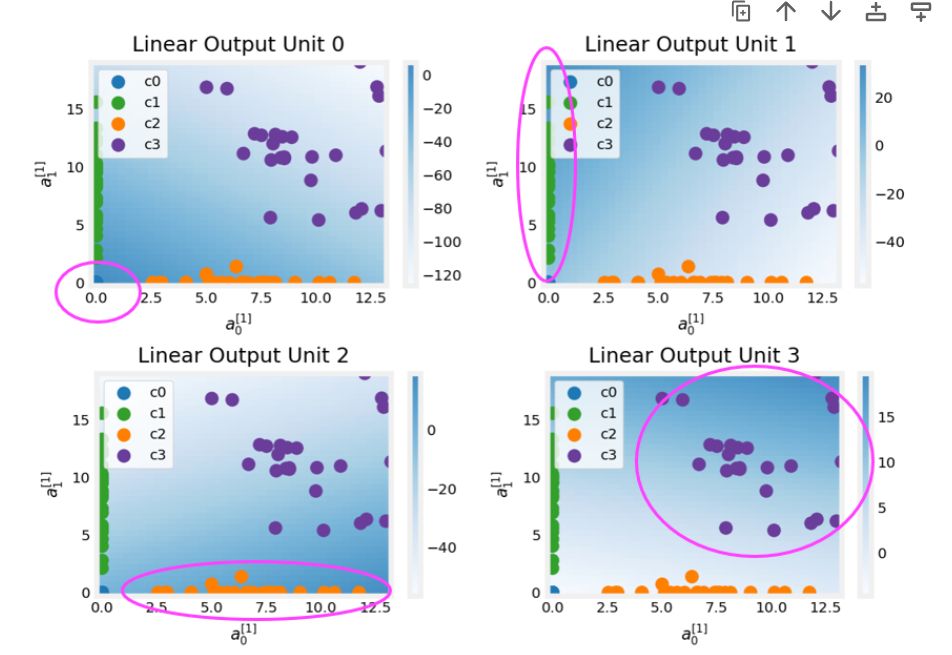
输出层:神经元个数等于分类个数
-
逻辑回归函数(softmax regression):
注:
- 和sigmoid一样,都是放在输出层
- 使用softmax而不是的好处有很多,
-
通过损失函数定义成本函数
-
改进:由于CPU计算的精度高于浮点数存储的精度,故不使用中间变量可以缩小计算误差
-
源代码
-
注:这一步的存储是导致误差放大的关键
-
-
-
修改后的代码
注:
-
这里合并了计算步骤,去除了中间存储的误差
-
进而导致修改最终输出为
linear,还需要额外进行一次softmax -
softmax避免溢出的实现:令,则可以有
思想:分数可以通过分子分母同乘除以避免分子分母单独计算时的溢出
-
显然第一项有溢出的风险,故同样令,可以简化为
=
思想:令,可以简化为
-
-
-
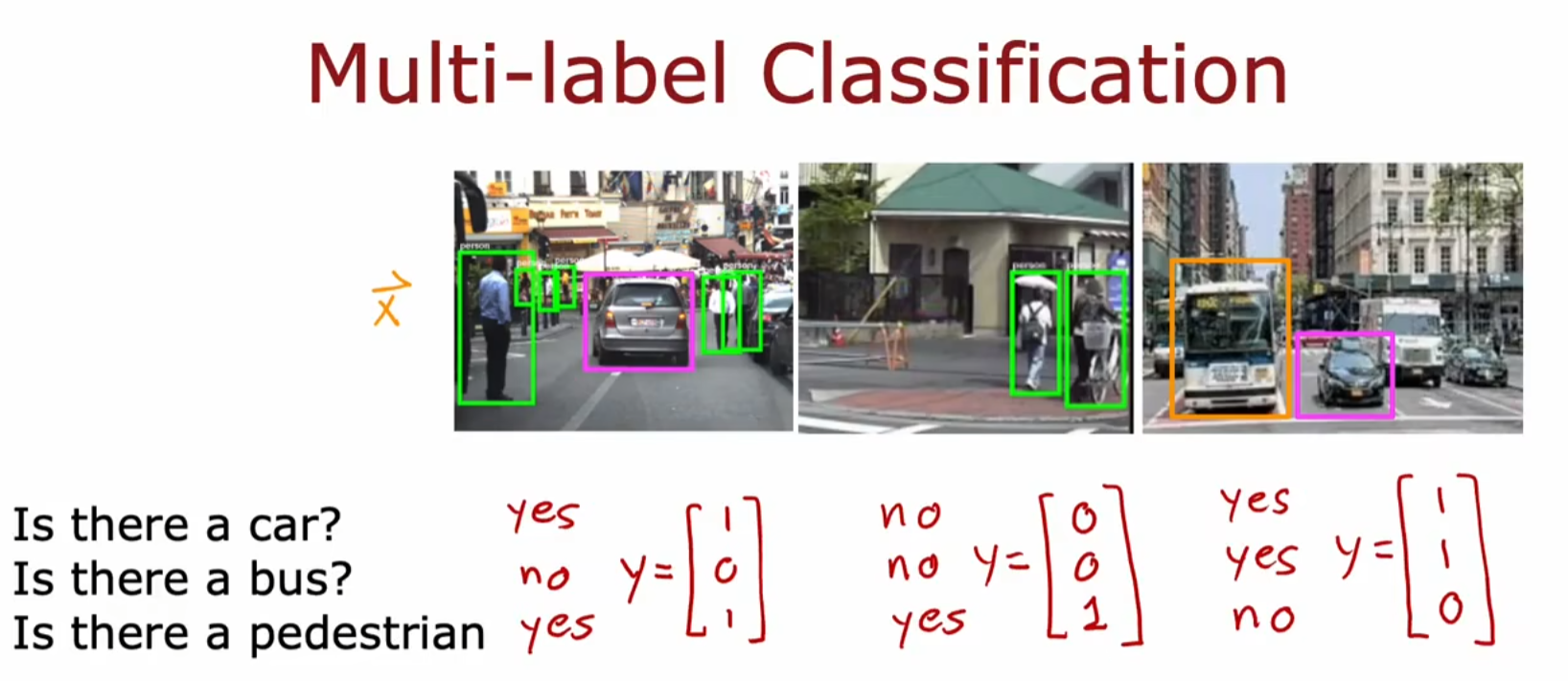
多标签分类:同时检测多个目标
思想:输出层有多个神经元
-
-
高级优化
-
梯度下降优化
Adam(Adam Algorithm Intuition):亚当算法,一般不断增加学习率参数,遇到震荡减小学习率参数
注:每个目标函数参数有自己的学习率参数
-
其它网络层
卷积层(convolutional layer):包含多个神经元,每个神经元对应原图像的子区间
优点:
- 加速计算
- 需要较少的数据拟合,且不容易过拟合
-
-
计算图:分解计算成本函数计算过程,tensorflow中用于自动计算导数,也说明了前向传播和后向传播的原理
6|0六、机器学习经验
-
偏差与方差
-
基本概念:直接对比欠拟合和过拟合理解,偏差与方差是欠拟合/过拟合的表示形式,欠拟合/过拟合是偏差与方差的本质
-
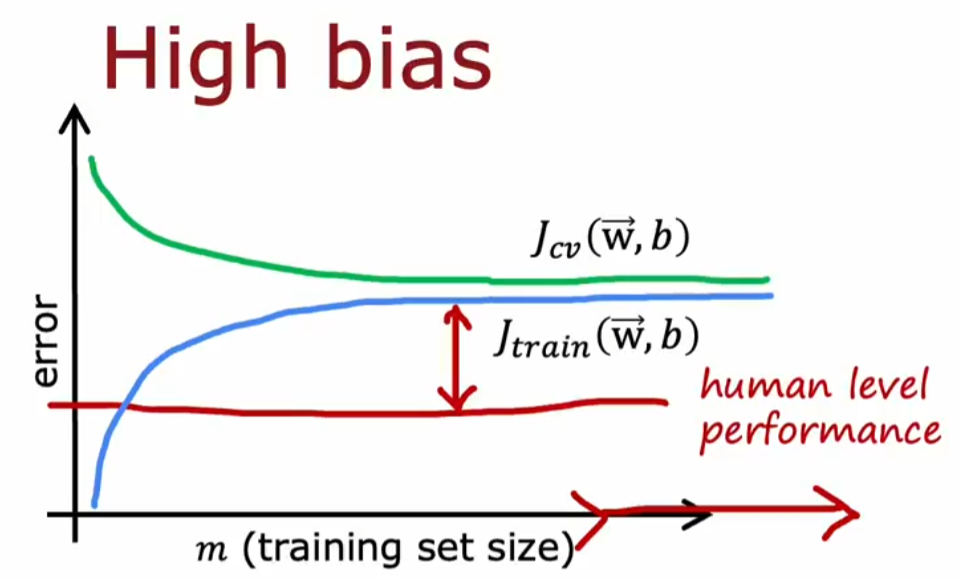
高偏差(bias)的表现:较大,较大,即欠拟合
-
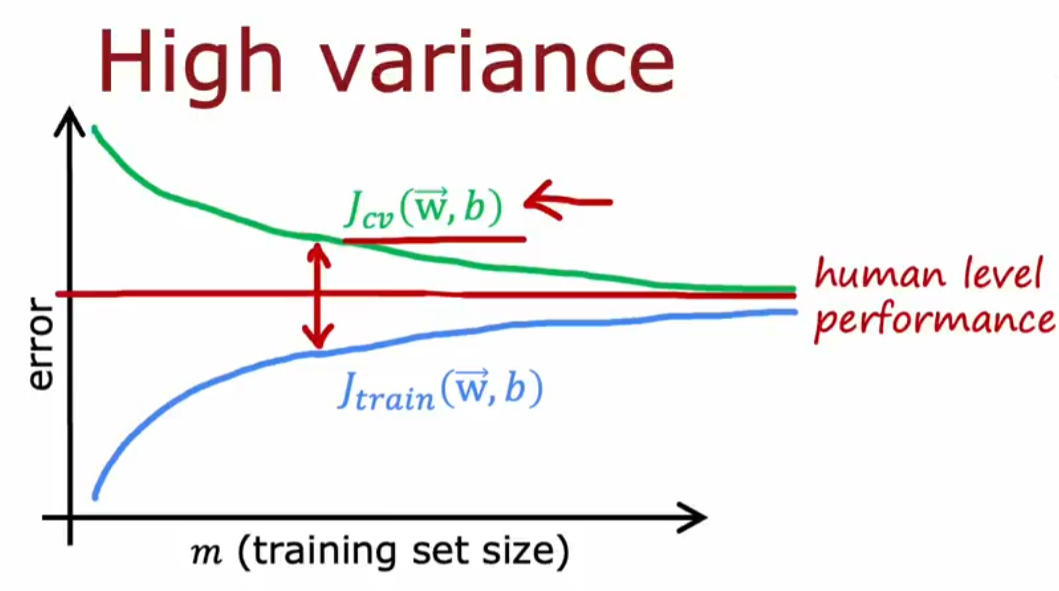
高方差(virance)的表现:较小,较大,过拟合
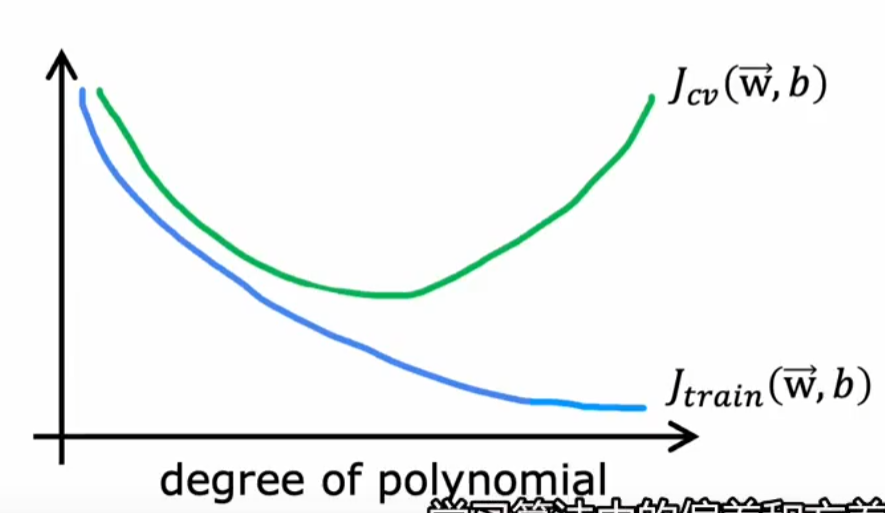
注:左侧欠拟合,右侧过拟合
-
-
多特征值模型的性能评估
- 分割数据集:如将0.6的数据作为训练集,0.2的数据作为交叉验证集,0.2的数据作为测试集
- 数据集使用:这里实际上可以理解为用训练集训练参数w和b,用交叉验证(Cross Validation)数据训练参数d——多项式阶数和选择模型,最终用训练数据评估最终选定的模型的泛化特性(Generalization)
- 数据集计算:
- 计算测试样例的误差:
- 计算训练数据的误差:
- 交叉验证集的训练方法:
- 制定性能评测标准
- 以人类自身能力为基准:假如人的标准值只有10.6%,,为10.8%,为14.8%。比较标准值和可知,偏差(bias)较小;比较和可知,方差(virance)较大;
- 其它已经实现过的算法:如果不能超过其它算法,当前所做的也就没有意义啊
-
数据集大小与偏差,方差的关系:结合学习曲线,即train数据集大小和的关系
注:绘制学习曲线的方法比较繁琐,实际用的不多,但需要清楚添加数据主要适用于高方差的情况
-
正则化参数与偏差,方差的关系:调制正则化参数,找到使最小,且相对小的值
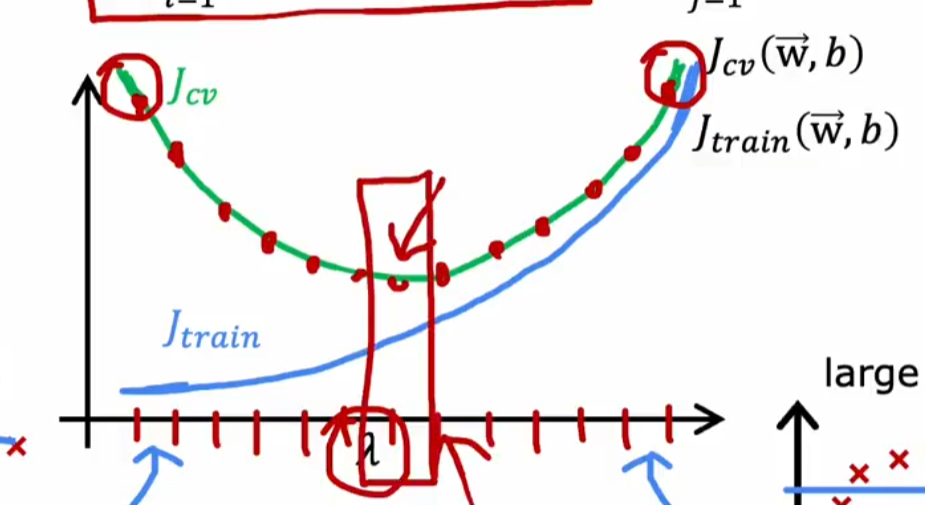
注:注意到上下两个图相似,实际上degree和的关系是,过大,degree则会尽量小(直接拟合为);过小(如等于0),degree则会尽量大
-
总结解决策略
- 获取更多数据:有助于解决高方差(过拟合)问题
- 增加选取的特征值:有助于解决高偏差(欠拟合)问题
- 减少选取的特征值:有助于解决高方差(过拟合)问题
- 使用多项式拟合:有助于解决高偏差(欠拟合)问题
- 增加正则化参数:有助于解决高偏差(欠拟合)问题
- 减少正则化参数:有助于解决高方差(过拟合)问题
注:
- 其实以上两个方面就是从数据和模型(包括特征值个数,正则化参数设置)两个角度出发解决问题
- 具体原因需要结合以下两块内容的解释
-
-
神经网络构建与偏差,方差的关系
- 第一步查看是否高偏差:若是,则构建更大的神经网络
- 第二步查看是否高方差:若是,获取更多数据
- 回到第一步,继续检查是否有高偏差
注:
- 在正则化运用得当的前提下,大型神经网络通常不会过拟合
- 缺陷在于需要更多的计算量
-
机器学习流程:以垃圾邮件识别的神经网络模型为例
-
确定模型,数据
-
获得数据:
-
例如通过钓鱼执法,使大量虚假的邮件地址被垃圾邮件运营商获得,进而获得大量的垃圾邮件数据
-
数据增强:修改原测试数据,获得新测试数据
-
图像数据:在原图像数据基础上放大,缩小,变形
-
语音数据:在原语音数据基础上添加噪音
-
-
数据合成:如利用电脑中的字体形成多种多样的文字图片
-
-
迁移学习(transfer learning)
- 流程
- 下载一个预训练好的模型:尽可能功能相似,如果我现在是想做一个数字和字母识别的模型,那我应该去找类似的比如动物识别的模型
- 根据已有的数据进行微调
- 若可用的测试数据集较小:只重新训练输出层
- 若可用的测试数据集较大:训练所有层
- 原理:模型的多个层次可以相互借鉴,例如对于物体识别
- 边缘检测层
- 角点检测层
- 形状检测层
- 流程
-
-
训练模型
-
诊断模型:错误诊断,根据主题,属性或特征对错误的数据集进行手动分组
例如一共有100个错误样例,其中:
- 医药相关:21
- 故意的拼写错误:3
- 非常规邮件地址:7
- 密码盗窃/钓鱼:18
- 图片:5
显然,可以重点解决医药相关和密码盗窃/钓鱼问题
注:
- 前提是人能对样例做出判断,例如对于什么样的广告人会点击,就很难做出人为判断,故不适用该错误诊断方法
- 分组并不需要保证不重不漏
- 如果错误的数据集比较大,可以从中抽出100规模的数据集进行分组,因为这能保证你在合理的时间能完成手动分组
-
这里开始慢慢变成了一个工程型问题,即先确定一个基本的模型框架,然后根据测试数据的结果
- 继续调整模型,以细化解决部分突出问题
- 继续获取数据,主要获得突出问题的测试数据
-
完整周期
- 确定项目目标
- 收集数据
- 训练模型
- 部署模型
-
政治,道德与伦理:再部署前进行审核
- 符合政治正确
- 符合道德
- 多样化
- 了解行业标准
- 指定
mitigation plan:如回滚版本,人工介入等
-
倾斜数据集(skewed data set)
-
存在问题:不同类别之间样本数量严重失衡的数据集,例如有关罕见病的数据集,倘若患有罕见病的概率是1%,此时模型预测的罕见病概率是0.5%,我们很难直观地说模型是否有效,因此需要借助额外的工具
-
构建混淆矩阵(Confusion Matrix)
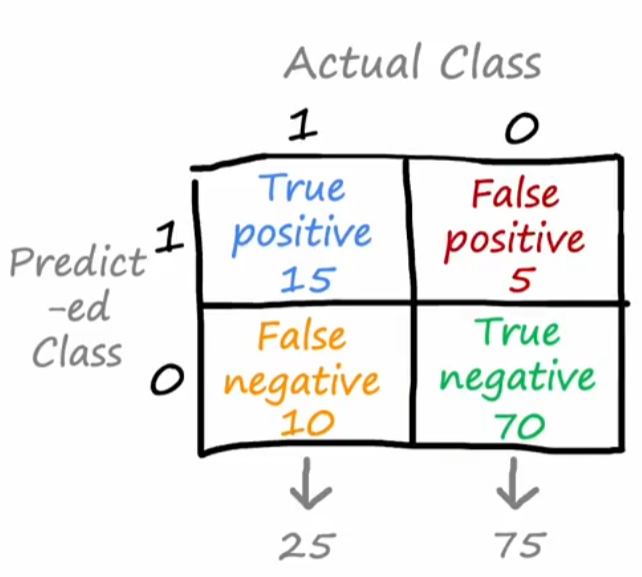
-
计算精度和召回率:通常两者都是越高越好,但实际上相互约束
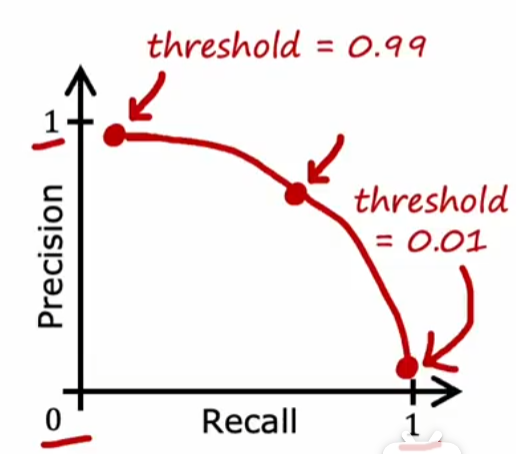
-
精度(precision):被预测病人中罕见病正确预测的百分比=
精度较低:提高threshold,即在可能性较大时才将其预测为病人 => 可能会导致低召回率
-
召回率(recall):实际病人中正确预测罕见病的百分比=
召回率较低:降低threshold,即在可能性较低时就将其预测为病人 => 可能会导致低精度
-
-
自动选定合适的threshold方法:使用算数平均数
思想:
- 选取a,b相对大一组数据:使用算数平均数
- 选取a,b相对大一组数据且惩罚较小的a或b:使用调和平均数
-
-
7|0七、决策树
-
决策树的基本概念
-
结构
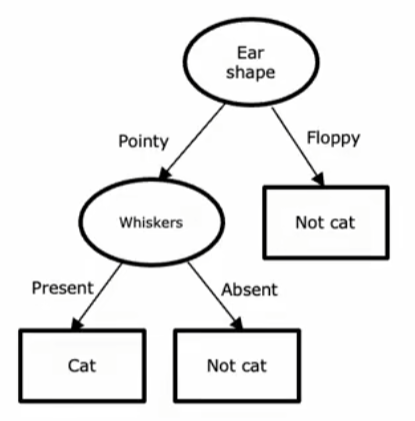
-
决策节点:非叶节点
-
叶节点:归入的分类
-
-
纯度,熵与信息增益
-
定义:只包含某个类的样本时最纯,包含每个类的样本一样多时最混乱。在数值熵,通常用熵来定义
-
作用:选择节点分裂的特征应该尽可能提高纯度,降低熵
-
熵公式(以两个类的样本为例):
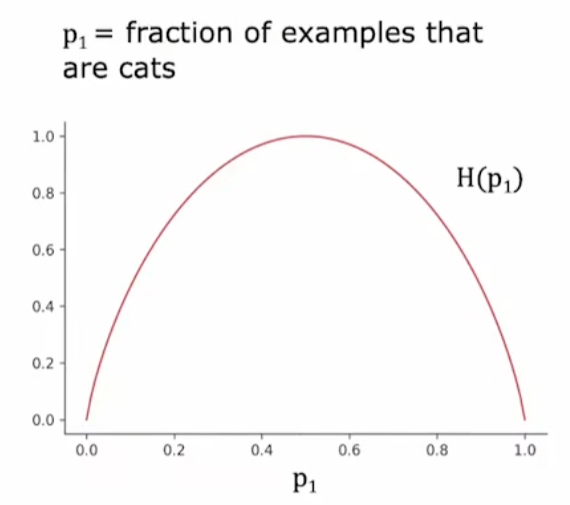
注:对称且中间高,两边低
-
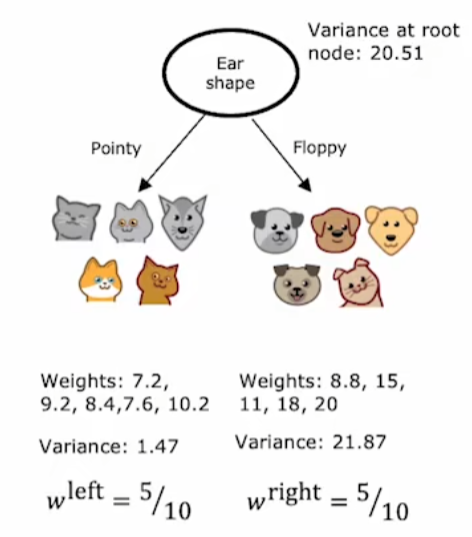
求采用某一个特征分类的熵:加权熵,按照当前特征划分后的熵

注:
-
左侧图片少画了一只狗
-
思想:当希望数量多的节点有更多权重,可使用加权平均。最后选取的可以是最低的,也可以是最高的,比如在本例中我们希望选取最低的
-
-
信息增益(Information gain):即父节点的熵减去子节点的加权熵
思想:有多个选择 => 建立选择标准(这里通过响应的函数Entropy) => 获得最好的选择
-
-
-
学习过程
-
选定特征:根据特征将当前节点的样本划分为两类,通常比较并选择纯度最高,权重熵最低,信息增益最高的特征
-
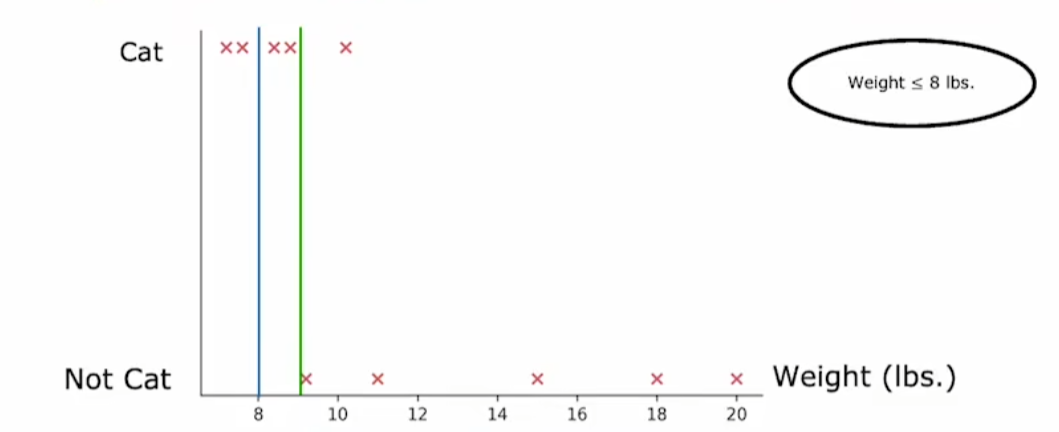
什么时候停止分裂
- 100%纯净
- 或者当前节点已经是最大深度:避免过拟合
- 信息增益低于某个阈值
- 节点个数低于某个阈值
-
将决策树泛化为回归树
-
-
树集成
-
决策树存在的问题:对微小变化高度敏感。即对原数据集做一个微小的变化,就能得到一个完全不同的决策树。
-
解决:针对一个待预测的数据集,使用多棵不同的决策树进行预测,最终选择得票最高的结果,这可以大大将强算法的鲁棒性
-
如何构建多个不同的决策树
-
数据集:有放回抽样,选取十个不同的样本放在一个袋子中,每次有放回地抽取十个样本,这十个样本中可能有重复
注:
- 可以看做每次选取的都是一个子集合(这里子集合,指相对于原先的去重集合)
- 基于的原理恰恰是决策树对微小的数据变化高度敏感,从而可以构建不同的决策树
-
构建决策树:随机森林算法
注:建议B在100左右,再大一点会造成边际效应递减,浪费计算资源
-
增加随机性:从n个特征中随机选取k个特征构建决策树,通常可以令
思想:当函数的构建对微小变化高度敏感时,可以修改数据集以构建多个不同的函数,比较预测的结果,最终选取概率最高的
-
-
XGBoost(eXtrme Gradient Boosting,极端梯度提升)
相对于随机森林的改进:在循环迭代过程中,选取数据集的时候有意识地选取前一轮构建模型中做得不好的数据集
好处:内置了正则化(参数)以防止过拟合
注:其实现及其复杂,一般还是直接调用库
-
几种方法的优缺点比较
-
决策树和树集成
- 通常用于表格数据(结构化数据)
- 训练速度快
-
多元神经网络:
- 可以处理多种数据结构类型,包括非结构化的数据
- 训练速度慢,但可以使用迁移学习加快速度
注:非结构化的数据指声音,视频,图像等
-
-
8|0八、无监督学习
-
聚类算法(Clustering):例如衣服厂商有一组身高和体重的数据,你希望将所有数据分成三组,以对应S,M,L三个型号
-
K-means算法
-
流程
- 随机初始化k个簇心(cluster centroids),等
- 将所有点根据簇心分配给最近的簇:通过计算点到簇心的距离
- 计算各簇的质心(通过平均求得),将簇心设置为质心
- 重复第二个步骤
-
极端情况(conner case):一个簇中没有任何点
- 簇个数直接减1:直接忽略0簇
- 重新选取初始化的簇心
-
优化目标:从成本函数的角度看k-means算法,可以用于初始化簇心
畸变函数(distortion function):
- :第i个簇
- :第i个簇的质心
- :样本点
- :样本点对应的簇心
问题:这一块内容有点没看懂
思想:
- 该方法还可以用来找任意一堆样本点的簇心
- 当一个算法是收敛(converge)的,那么对应的成本函数应该递减的
-
初始化簇心:结合优化目标中的成本函数
- 随机确定k个簇心的位置
- 计算对应的成本函数
- 重复上述过程多次(50-1000次),选取成本函数最低的一次做为起始位置
-
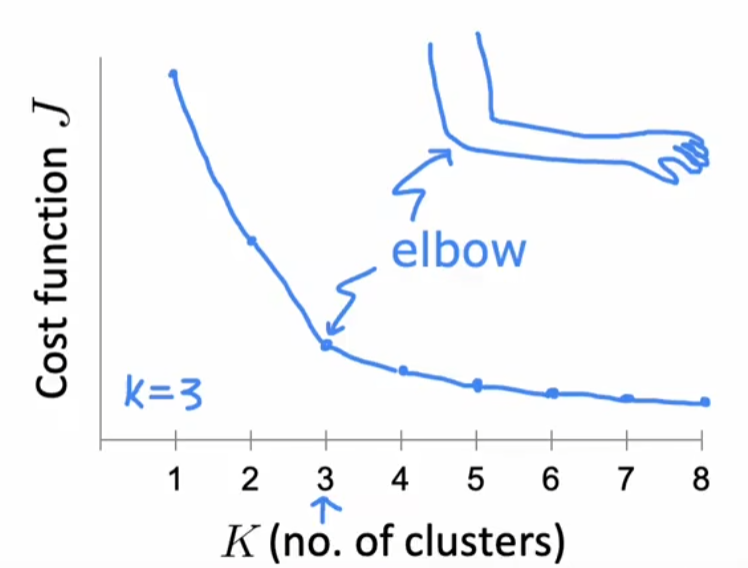
选择聚类数量:
-
-
异常检测算法(Anomaly detection algorithm):根据用户登录频率,操作频率等信息检测用户行为是否可疑,进而对用户进行安全限制等操作
-
正态分布(Gaussian/Normal Distribution):适用于只有一个特征的情况
-
公式:
- :均值
- :方差。方差越小,数据越向均值集中;方差越大,数据越向均值偏移
-
样本参数估计
-
-
注:
- 这里了使用是因为在估计时已经用了一个自由度
- 求总体参数只存在于理论上,实际我们只能求样本参数
-
-
-
算法实现
-
计算样本参数
-
计算
注:显然上式是基于是独立的,但事实上根据经验即使不独立上式也能较好运行
-
若,将其标记为异常(Anomaly)
-
-
实数检测(real-number evaluation):通过划分数据集评价一个异常检测算法
划分数据集:训练集,交叉验证集,测试集
- 训练集:可以不包含异常数据(
y_hat) - 交叉验证集:包含异常数据,用于调制等参数
- 测试集:包含异常数据,当数据集量较小时可以没有以帮助更好地调整参数,但可能会导致过拟合(泛化效果较差)
- 训练集:可以不包含异常数据(
-
选择特征
-
好的特征:呈正态分布
-
非正态分布的特征:尝试通过函数转换为正态分布,如使用
-
根据异常样例增加新的特征:如分析交叉验证集中的某个异常样例,发现出现该样例的原因是较大,则可以增加此组合特征
注:实际上就是根据结果找原因,且需要在采用这种方法的过程中考虑一定的泛化性
-
-
监督学习与异常检测比较
- 使用监督学习
- 有错误数据集或反例在样本中占比较小
- 正向学习异常行为
- 使用异常检测:
- 无错误数据集或出错的原因可以是多种多样的
- 反向排除所有异常行为
- 使用监督学习
-
-
9|0九、推荐系统
9|1协同过滤算法(Collaborative filtering)
基于用户评价和物品特征
基于用户评价:根据用户购买的物品,推荐相似的用户购买的物品
基于物品特征:根据用户购买的物品,推荐相似产品
注:这里相似是根据用户的购买记录,评分等构建的
-
基于非二进制标签:电影打分系统
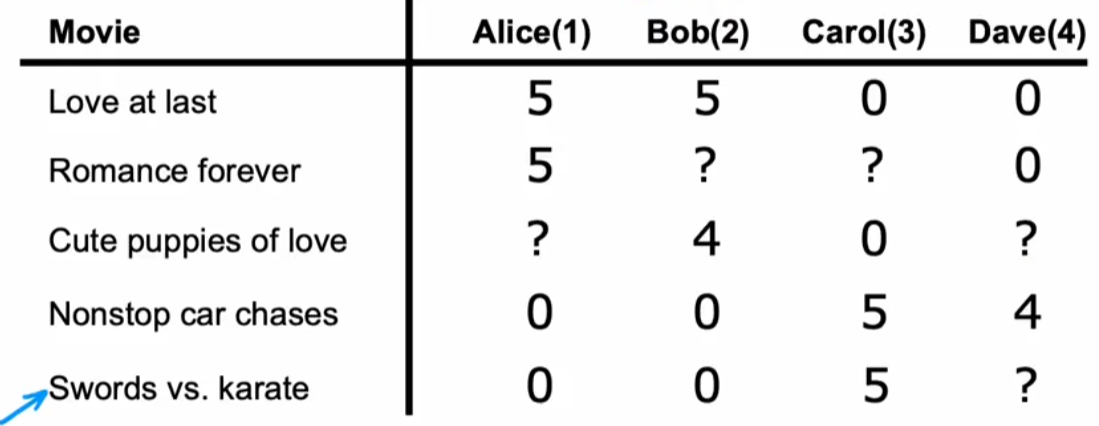
注:对于未定义的数据:使用专门的矩阵进行存储是否有定义
-
构建电影的特征向量:在本例中可以构建浪漫值,动作值两个特征,显然这两个也是待定参数
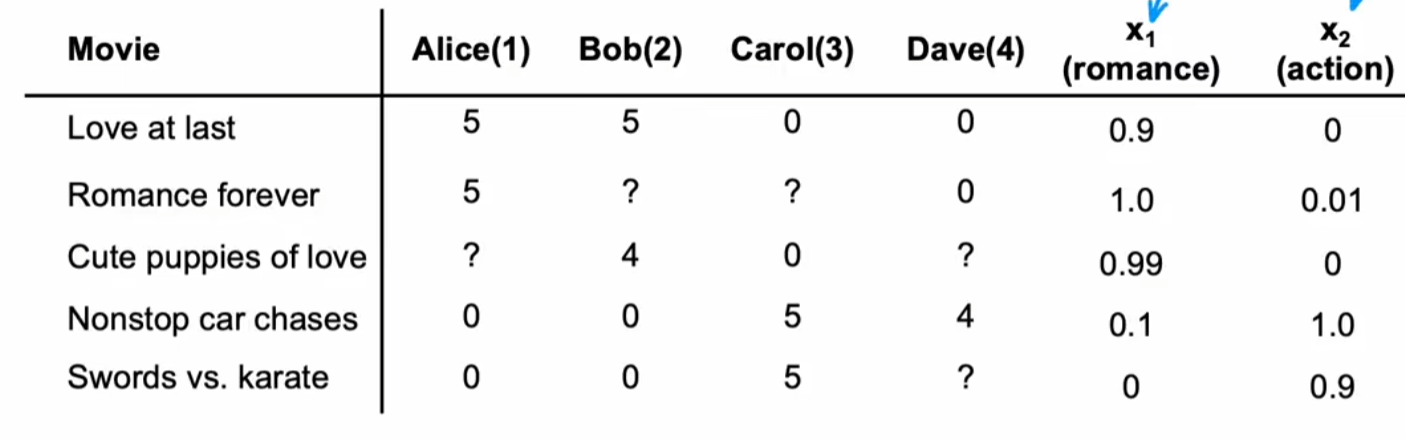
问题:我们是否可以确定两个极端的表示romance,action参数的电影,进而反过来通过用户确定其它电影的roman,action的参数,这似乎是一个很有趣的想法?
-
构建目标函数:
注:参数可以看做用户对特征的偏好,用户的特征向量
-
使用均方误差构建参数的成本函数
r(i,j):布尔值,表示是否打过分,这里实际上只计算了打过分的电影y^{(i,j)}:打过的分w^{(j)},b^{(j)}:评分X^{(i)}:电影的特征向量,比如浪漫值,动作值等
注:实践证明这里最后除以而不是更好
-
使用均方误差构建参数x的成本函数
-
协同过滤(collaborative filtering)
- 成本函数:
- 梯度下降:同时更新,w,b,x
-
-
基于二进制标签
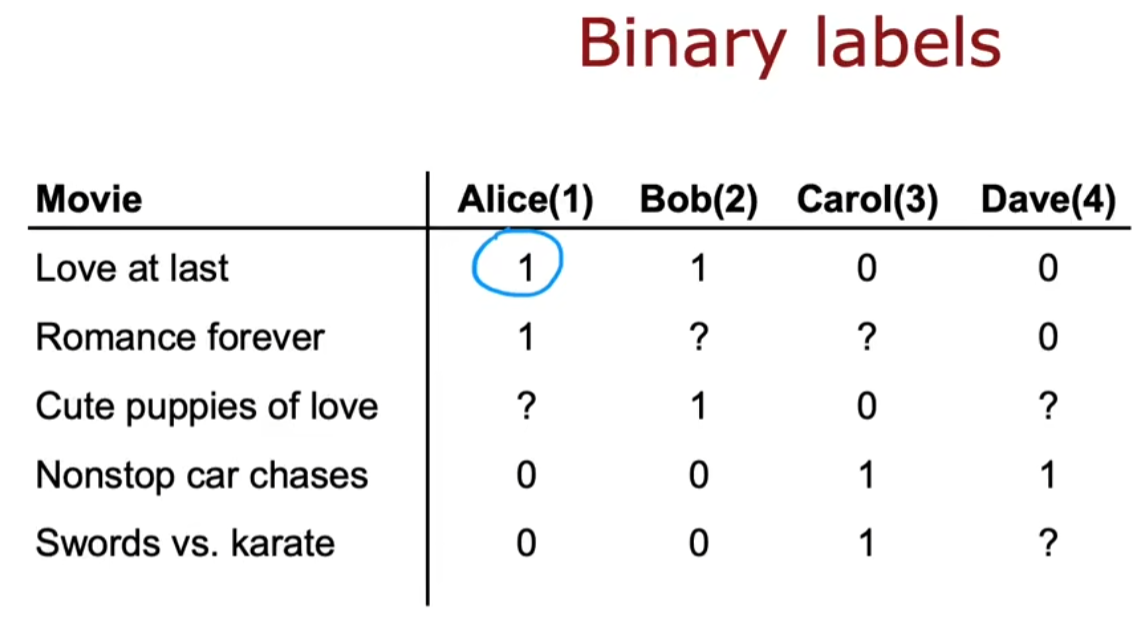
-
目标函数:
注:
-
相同的损失函数:
-
相同的成本函数:
问题:为什么这里的成本函数中没有加正则化参数
注:
- 和传统的深度学习算法的区别在于,x也是一个待定的参数
- 可以参考linear regression到logistic regression
-
-
均值归一化(mean normalization)
-
问题的出现:以非二进制标签为例
- 由于成本函数J计算的仅仅是用户打过分的电影,故对于没有给任何电影打过分的用户,其对应的参数显然会被优化为0向量,进而该用户对其它电影打分的预测值恒为0,显然这不符合事实逻辑。
- 一个比较好的方案是,当该用户打分数据较少时而无法预测评分时,我们希望直接使用大众评分
-
计算
-
问题的解决
则在预测时,我们可以这样计算,
此时,当仍然为0,最后的预测结果将会是均值
-
-
使用限制
- 冷启动问题:参考电影评分系统,主要由数据不足导致
- 一部电影没有多少人评价过
- 一个人没有评价过多少电影
- 使用的都是边缘信息:与电影内容和用户的偏好不直接相关
- 电影:预算,工作室等
- 用户:用户肖像(年龄,性别,地址等)
- 冷启动问题:参考电影评分系统,主要由数据不足导致
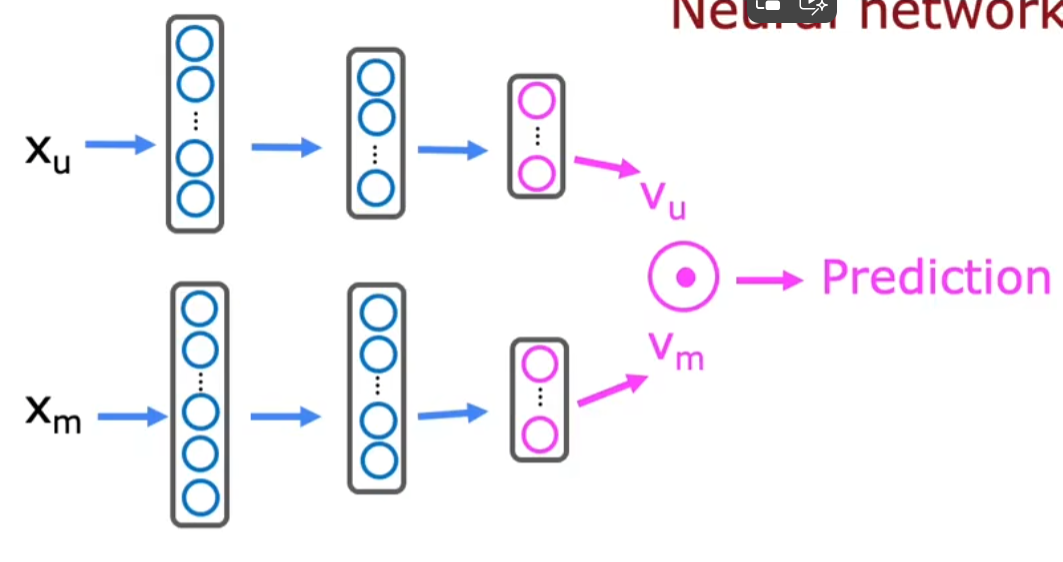
9|2基于内容的过滤(Content-based filtering)
特点:
- 和基于物品的协同过滤相同:协同过滤中只有用户评价数据,而基于内容的过滤中既有用户评价数据也有用户/物品特征数据
- 用户特征和项目特征比较:用户特征向量可能会非常大
大型推荐系统的实现:
- 检索(retrieval):根据相似度检索获得一个可能的候选清单,并清洗数据去掉重复的,无效的(如已经购买过的)
- 排名(ranking)
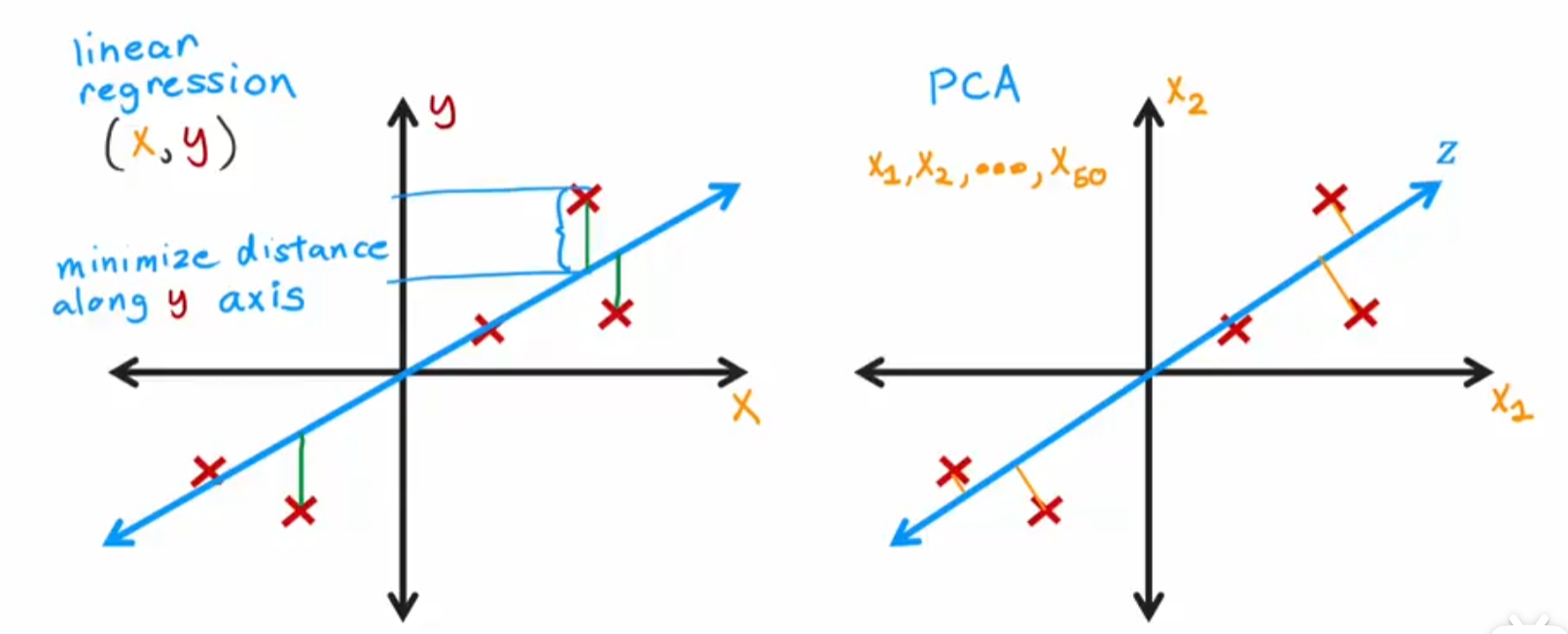
9|3主成分分析(Principal Component Analysis,PCA)
作用:用于对多维特征的可视化
-
二维坐标下的表示
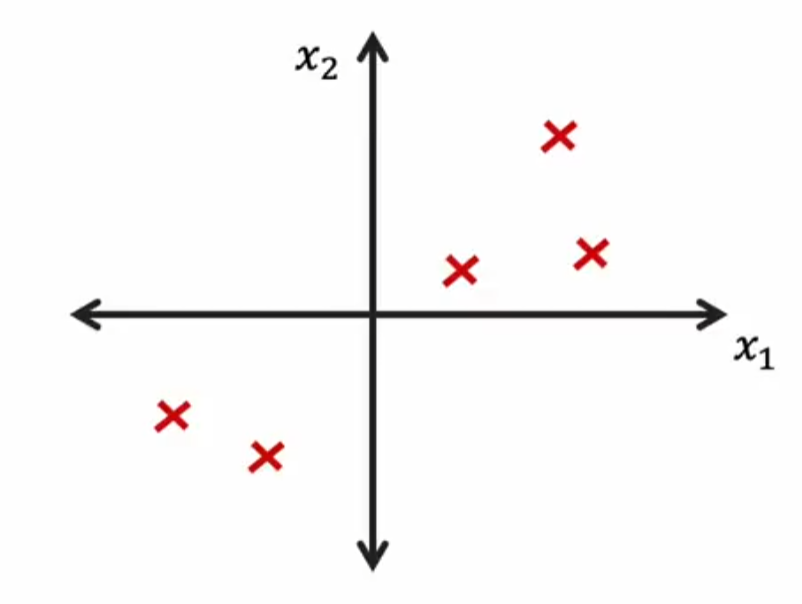
-
尝试在二维坐标中找到一个轴(对应的单位向量为),将所有点(对应的点坐标向量为)都投影到该轴上:在新坐标轴上的位置为
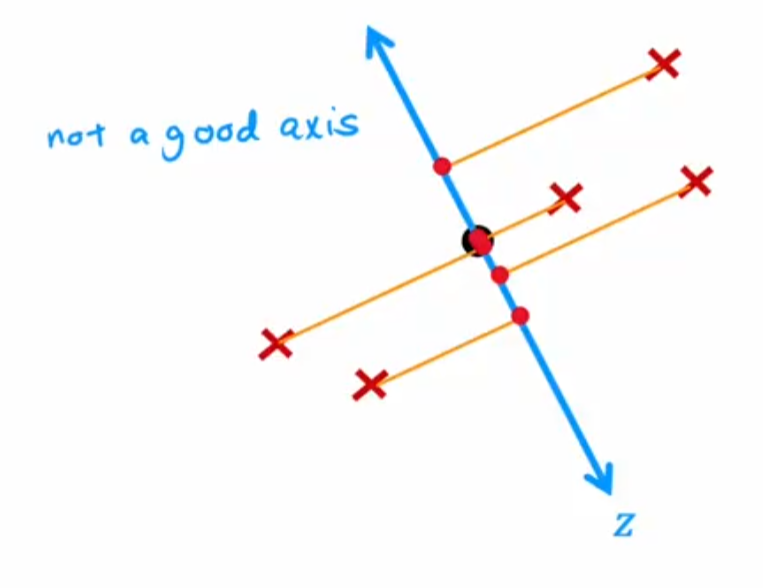
选择主成分的依据:方差,正交性等
-
PCA与线性回归的比较:linear成本函数所求的是y值差距,PCA所求的是距离
-
PCA的重建:近似求原值,即
-
代码实现
10|0十、强化学习(Reinforcement Learning)
-
基本概念
-
出现的原因:某些场合可能获得数据集困难
-
基本想法:通过正负反馈进行学习
-
马尔科夫决策过程(Markov Decision Process):当前状态 => 执行的动作 => 回报(奖励或惩罚) => 下一个状态
-
折扣因子:,对于第n步得到的奖励需要乘以
注:可以认为是用于惩罚较远的奖励
-
策略PI:一般期望用于获得最高的回报
-
状态-动作方程,遍历可能得结果,然后选取最佳
-
-
贝尔曼方程(Bellman Equation)/动态规划方程
方程:
- s:状态,代表下一个状态
- a:动作
注:这里的要点是
当前的结果=当前的奖励+之后的最好结果,这里的要点是之后的最好奖励是可以通过递归获得的 -
奖励机制的设定:根据进程设定,但需要设定恰到好处的奖励数值
-
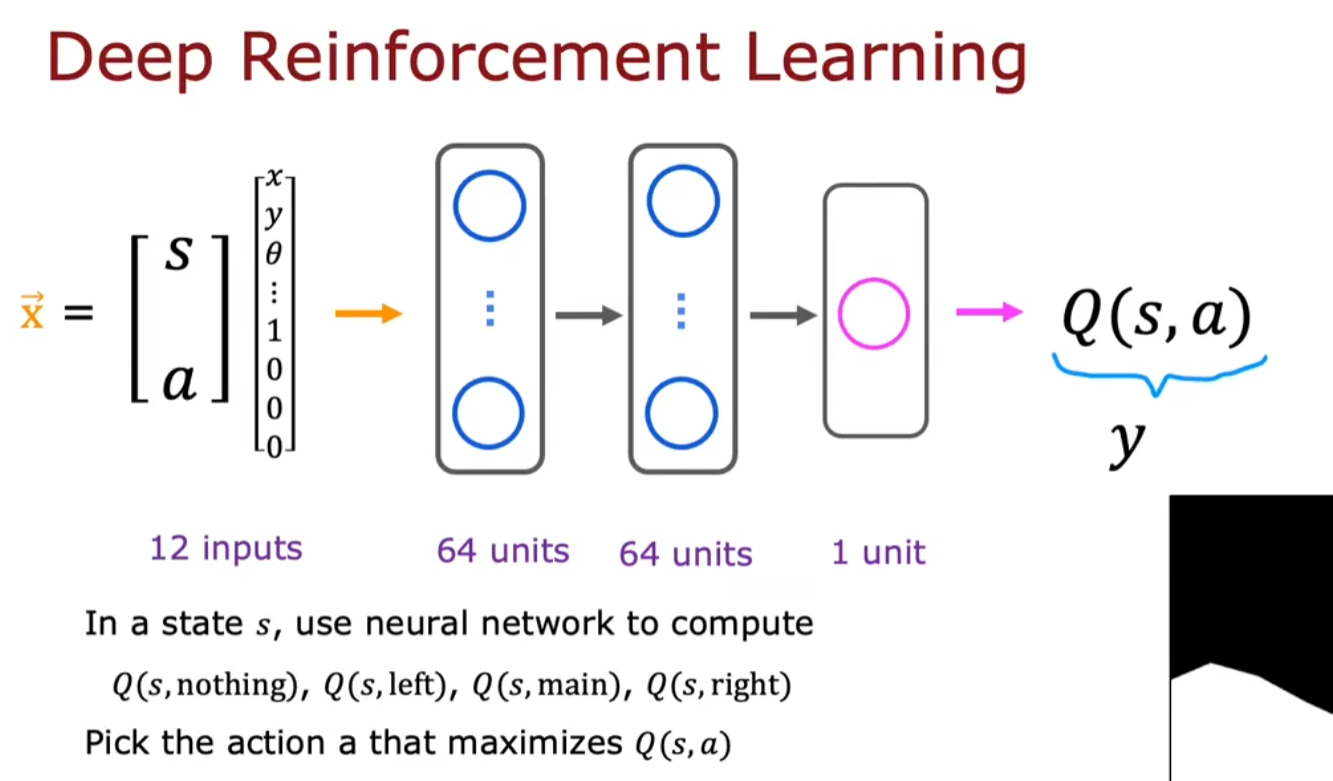
学习状态函数:通过神经网络训练
注:训练方式是一个动作一个动作地训练
-
算法优化
-
-贪婪策略:增加随机动作,跳出局部最优
-
小批次梯度下降(min-batch gradient descent):适用于大量的数据,与普通的梯度下降的不同
- 普通的梯度下降:每次使用相同的所有数据做梯度下降
- 小批次梯度下降:每次使用一部分数据做梯度下降,且每次数据不同
优点:高效
想法:是否可以通过随机的x创造对应的y样本,然后筛选出其中好的样本进行学习
-
软更新:每次在更新参数时只做小的更新,
-
-
英语名词
-
deep learning
- regression
- classification
-
mathematic
-
difference:差值 -
mean:平均值 -
slope:斜率 -
intercept:截距 -
derivative:导数 -
dot product:点积 -
J(wb) respect to b:J相对于b的导数 -
polynominal terms:多项式 -
标量与向量
scalar:标量vector:向量
-
convex function:凸函数 -
Converge:收敛 -
quadratic function:二次函数 -
variance:方差 -
standard deviation:标准差 -
矩阵
transpost:转置 -
numerical round-off:数值舍入错误
-
-
scatter plot:散点图 -
contour plot:等高线图,可以用来查看梯度下降过程中收敛的趋势 -
quiver plot:矢量图 -
comments:注释 -
feature:通常指入参x的种类数 -
objective function:目标函数 -
cost function:成本函数 -
loss function:损失函数 -
J of w and b: -
project:投影 -
perpendicular:垂直,90度
-
-
机器学习中的一次线性函数释义:
- 可以看做是一个基值
- 可以看作是变量的影响因子
-
Numpy的优点:并行计算
-
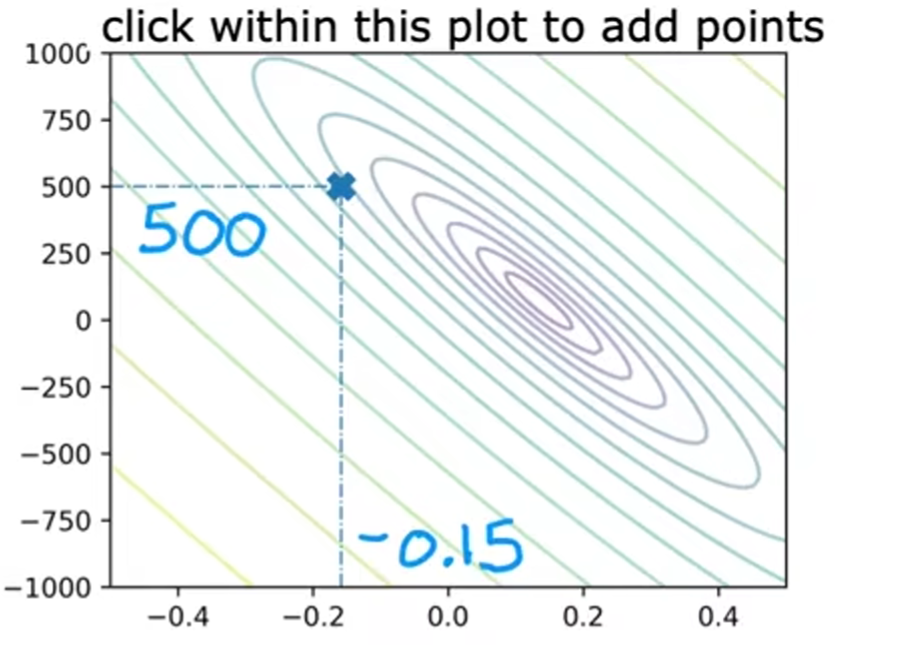
等高图查看
- 线间隔:表示数据的分界
- 线密度:线越密集数据变化越剧烈,相反线越系数数据变化越平缓
- 线形状:原型表示数据均匀变化,椭圆形表示长的一侧变化慢,窄的一侧变化快
-
标准差和方差
方差的计算公式
- 总体:
- 样本:
注:总体是理想情况下的,样本是实际情况下的
区别:标准差是方差的开根
-
平均数:平均数左右两侧分布的值个数相同
-
闭式解(closed-form solution):是指通过代数运算直接计算出的解析解
-
函数
- 定义域:
- 值域:
注:可知,函数单调递增
-
ln函数
- 定义域:
- 值域:
-
线性回归与逻辑回归的一般流程
-
(特征工程)
注:
()表示可选项 -
构建目标函数类型:如线性回归函数或逻辑回归的函数
-
构建正则化的成本函数
-
构建正则化的梯度下降:得到对应的参数
-
使用目标函数预测
-
-
向量点乘和矩阵乘法比较
-
向量乘法
-
输入:两个n维列向量或行向量
注:由于列向量和行向量必然都是,所以只需要n相同即可,但可以是
-
结果:一个标量
-
-
矩阵乘法
- 要求:对于,要求A的列向量数等于B的行向量数
- 结果:一个矩阵
- 要求:对于,要求A的列向量数等于B的行向量数
-
-
链式求导(chain rule):
-
浮点数表示上限
-
根据IEEE754,双精度浮点数一共六十四位,其中:
- 符号位:一位
- 指数位:十一位,移码表示,偏移值为1023
- 尾数位:五十二位
-
指数位上限:
注:表示十一个1位,由于全0和全1有特殊含义再减去1,最后减去移码的偏移值1023
-
-
-
diminishing return:边际收益递减 -
可以结合异常检测算法,整理一下假设检验的流程
-
question mark:? -
syntax:在程序中一般指语法 -
prime:'
__EOF__
本文链接:https://www.cnblogs.com/Arno-vc/p/18319373.html
关于博主:评论和私信会在第一时间回复。或者直接私信我。
版权声明:本博客所有文章除特别声明外,均采用 BY-NC-SA 许可协议。转载请注明出处!
声援博主:如果您觉得文章对您有帮助,可以点击文章右下角【推荐】一下。您的鼓励是博主的最大动力!

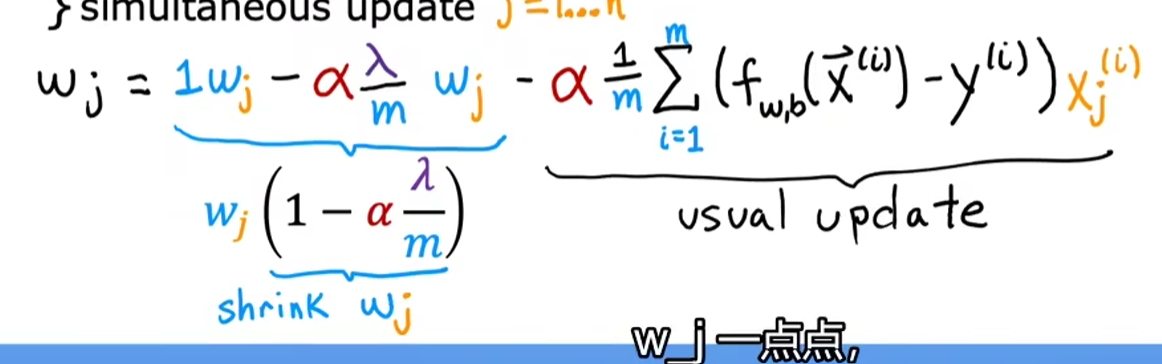




【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· Manus重磅发布:全球首款通用AI代理技术深度解析与实战指南
· 被坑几百块钱后,我竟然真的恢复了删除的微信聊天记录!
· 没有Manus邀请码?试试免邀请码的MGX或者开源的OpenManus吧
· 园子的第一款AI主题卫衣上架——"HELLO! HOW CAN I ASSIST YOU TODAY
· 【自荐】一款简洁、开源的在线白板工具 Drawnix
2020-07-23 Mybatis数据库分页
2020-07-23 Mybatis中Log4j日志的使用
2020-07-23 Mybatis结果集ResultMap映射
2020-07-23 Mybatis中的基本对象的生命周期和作用域