动态规划

根据百度百科，动态规划是运筹学的一个分支，是求解决策过程最优化的一个过程。本篇文章主要包含了其使用的三个前提条件(最优子结构，重叠子问题，无后效性)的理解，及通过编程解决一些简单问题过程中相关数组的构建，递推方程的求解，初值的定义。由于个人问题能力所限，对于动态规划问题的理解可能还不够深入，欢迎指出问题！

实例：超级楼梯问题

1. 原题链接：Problem - 2041 (hdu.edu.cn)
2. 题面：有一楼梯共M级，刚开始时你在第一级，若每次只能跨上一级或二级，要走上第M级，共有多少种走法？
3. 分析：斐波那契数列套皮

前提

1. 无后效性

   • 简析：前面的状态不会影响后面的状态

   • 与迷宫问题比较：

     • 超级楼梯问题：无论到第N(N<M)级楼梯是怎么走的，总是能到达第M级楼梯

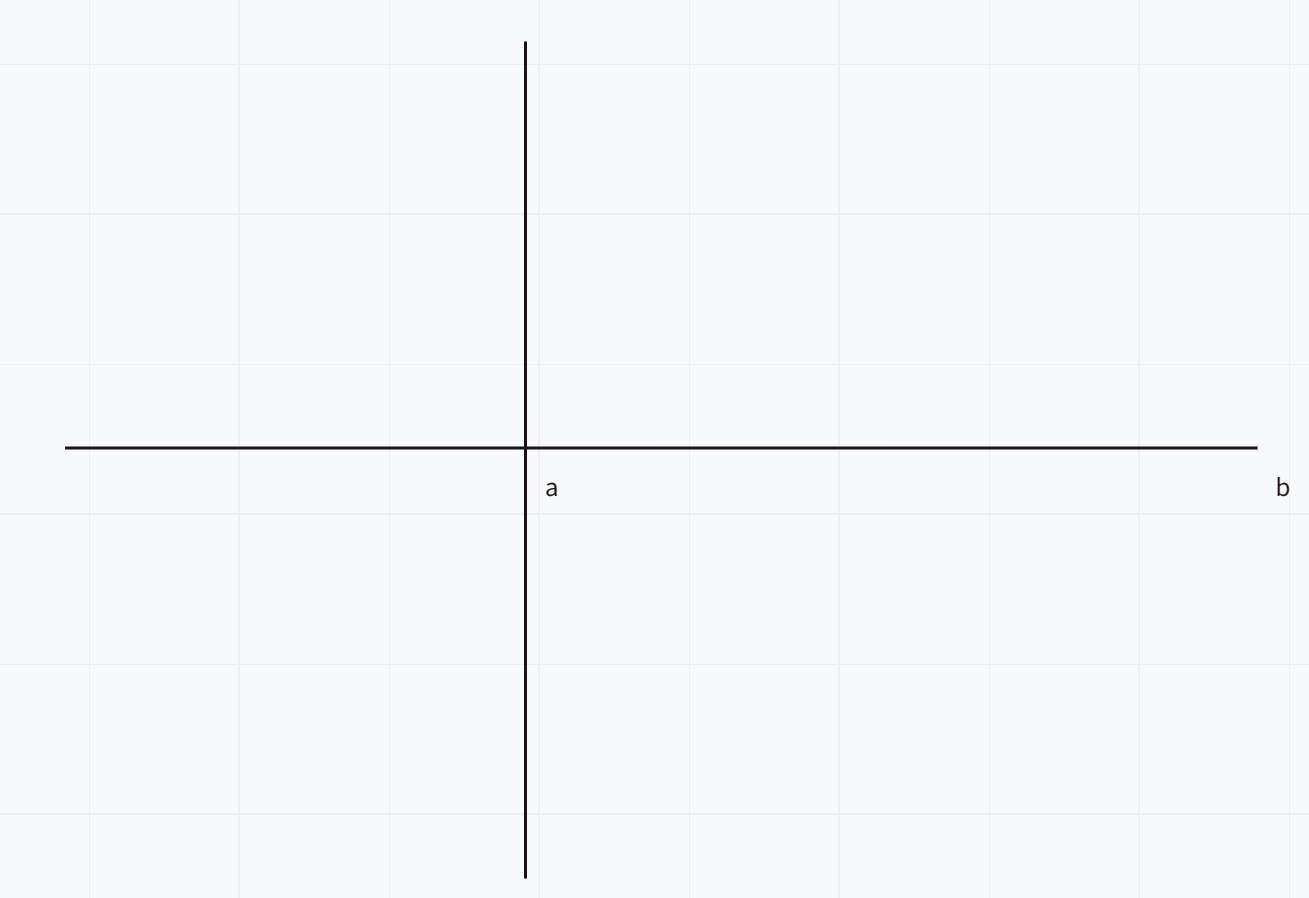
     • 迷宫问题：假设我们求从迷宫的起点a到终点b的最短路径，显然有迷宫的起点a选择的第一个方向会直接影响是否能到达b地点，即有后效性

       

   • 无后效性转为有后效性：增加维数

     注：见HDU 2045:不容易系列之(3)—— LELE的RPG难题(动态规划) - Arno_vc - 博客园 (cnblogs.com)，本质是修改动态规划求解的命题，最后通过分类讨论获得自己想要的解

2. 最优子结构

   • 简析：设目标问题为A，子问题为\(B_n\)，且\(A=f(B_1,...,B_n)\)，要求目标问题A的最优解，只需求子问题\(B_1,...,B_n\)的最优解

     以超级楼梯问题为例，目标问题为A：到达第M级楼梯，可分解为两个子问题

     • \(B_1：\)从第M-1级楼梯跨1级台阶
     • \(B_2：\)从第M-2级楼梯跨2级台阶

     故有\(A=f(B_1,B_2)=B_1+B_2\)

     注：函数\(f\)通常为相加，求最大值或最小值

   • 无法划分为最优子结构的问题

     • 参考：动态规划的最优子结构问题，有什么样的问题它不满足最优子结构？

     • 以无权有向图求最长边为例

       

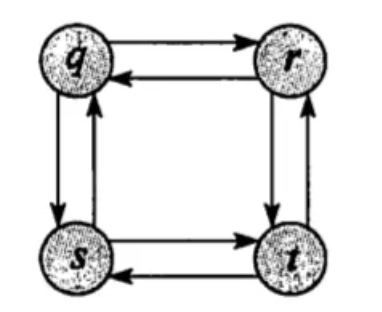
       • 目标问题：q到t的最长边为\(q => r => t\)
       • 子问题：若为最优子结构有q到r的最长边为\(q => r\)，但实际上q到r的最长边为\(q => s => t => r\)
       • 总结，该问题不满足最优子结构

3. 重叠子问题

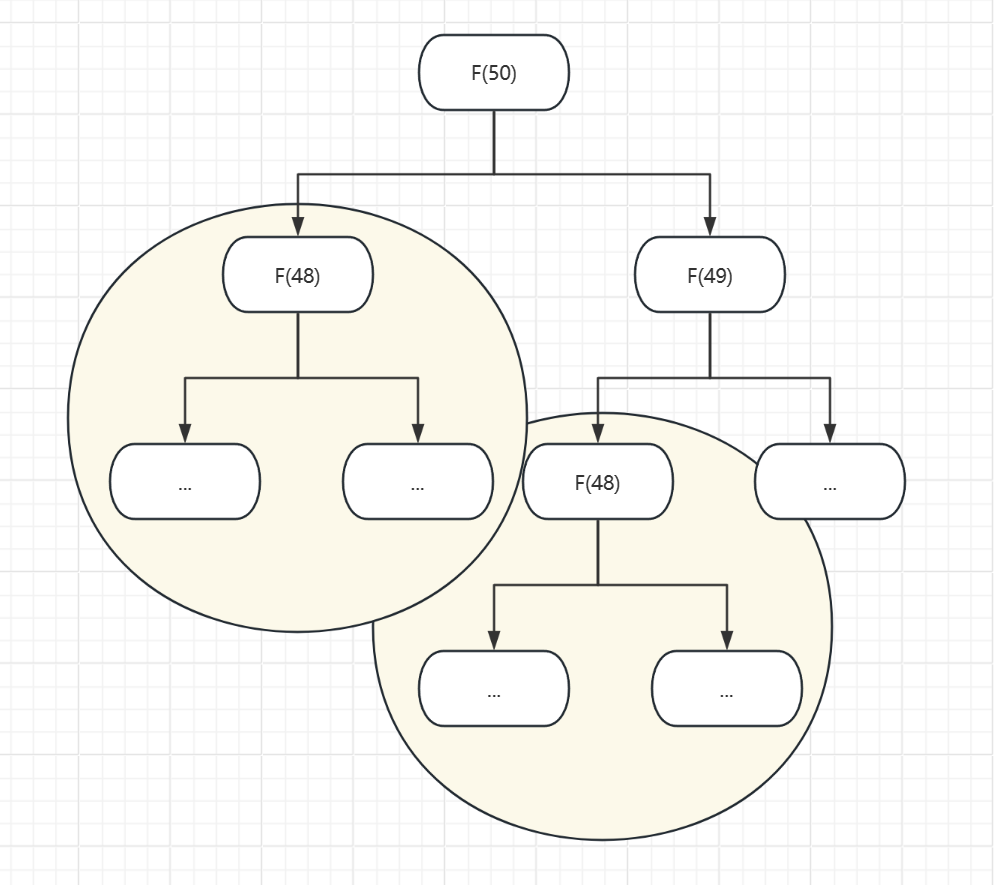
   • 从数学建模问题的角度，超级楼梯问题本质上是个斐波那契数列问题，可以看到在对于\(F(50)\)的计算过程中，\(F(48)\)有两次的重复计算。实际上，越下层的重复计算越多

     

   • 采用递归方式进行计算：计算所用的时间将会呈指数倍增长,且由于计算机内存空间的限制，函数递归可能会有爆栈风险(Runtime Error)。

     code

     #include <bits/stdc++.h>
     
     #define PI 3.1415927
     
     using namespace std;
     typedef long long ll;
     
     ll f(ll now){
         if(now==1||now==2){
             return 1;
         }
         return f(now-1)+f(now-2);
     }
     
     int main()
     {
         int n;
         cin >> n;
         while(n--){
             int m;
             cin >> m;
             cout << f(m) << endl;
         }
         return 0;
     }
     

   • 解决方法：递推方程(见下)

   注：当第n个阶段的状态仅与第n-1个阶段的状态有关时，可以认为没有重叠子问题，但依然可以通过动态规划求解

解决

1. 数组的构建

   dp[i]：到达第i个台阶的总可能数

2. 递推方程的求解

   • 到达第M个台阶只有两种可能：

     • 从第M-1级楼梯跨1级台阶
     • 从第M-2级楼梯跨2级台阶

   • dp[M]=dp[M-1]+dp[M-2]

3. 初值的定义

   • 易知dp[3]=dp[2]+dp[1],dp[2]=dp[1]+dp[0]，而dp[0]不合要求，故只需求边界dp[2],dp[1]
   • 到第二个台阶有两种可能，到第一个台阶有一种可能：dp[2]=2,dp[1]=1

4. code

   #include <bits/stdc++.h>
   
   #define PI 3.1415927
   
   using namespace std;
   typedef long long ll;
   
   int main()
   {
       ll n,ans[50];
       memset(ans,0,50*4);
       ans[1]=1;
       ans[2]=1;
       ans[3]=2;
       for(int i=4;i<50;i++){
           ans[i]=ans[i-2]+ans[i-1];
       }
       cin >> n;
       while(n--){
           int m;
           cin >> m;
           cout << ans[m] << endl;
       }
       return 0;
   }
   

补充

1. 一维动态规划：递推

2. 满足无后效性，最优子结构但不具有重叠子问题性质的问题：分治

   如：二分法求最值

3. 不满足无后效性：回溯