高数概念(待整理)
整个微积分以极限做为工具研究函数的性质,而极限本质上表达的是数列或函数上无数点这个特殊的集合在极限点的ϵϵ范围内(如果有极限)
- 复习:重点不在于记忆知识点本身,而在于考虑如何优化
- 可以做的专项
- 等价无穷小:可以和无穷积分,正项级数的敛散性相结合
- 放缩:可以和数列收敛,级数收敛,微分中值定理等题目相结合
- 递推关系式:数列难点
- 不等式:单调性,拉格朗日,最值,泰勒,凹凸性
高数概念提纲
- 函数
- 基本初等函数
- 函数的性质
- 单调性
- 奇偶性
- 周期性
- 有界性
- 极限
- 函数极限与数列极限的定义
- 极限的性质
- 有界性
- 保号性
- 极限的收敛性证明
- 夹逼定理
- 单调有界准则
- 无穷小
- 无穷大和无界
- 连续与间断点
- 闭区间连续函数的性质
- 有界性
- 最值定理
- 介值定理
- 零点定理
- 导数
- 微分中值定理
- 等式:罗尔定理,拉格朗日中值定理
- 不等式:拉格朗日余项的泰勒公式
- 微分中值定理
- 一元函数积分学
- 变上限积分
一、函数,极限与连续
函数
-
函数类型
-
基本初等函数
-
幂函数:xnxn
- n<0n<0:x≠0x≠0
- 0<n<10<n<1:x>=0x>=0
- n>1n>1:x∈Rx∈R
-
指数函数:ax>0(a>0,a≠1)ax>0(a>0,a≠1)
-
对数函数:lnx(x>0)lnx(x>0)
-
三角函数:tanx(x≠±nπ2,n∈N∗)tanx(x≠±nπ2,n∈N∗)
-
-
复合函数:内层函数的值域与外层函数的定义域有交
-
反函数:一般函数的定义域和值域的关系为多对一,反函数的定义域和值域的关系为一对一
-
分段函数:注意绝对值函数
-
有理函数:多项式加减乘除得到的函数,包括分数
-
参数方程形式的函数
{y=f(t)x=g(t){y=f(t)x=g(t)显示化为y(x)y(x)
- 法一:反解t=g−1(x)t=g−1(x),则y(x)=f(g−1(x))y(x)=f(g−1(x))
- 法二:找两个关系的关系,通常用于极坐标下的参数式
注:不能认为y(x)=f(g(t))y(x)=f(g(t)),因为f(t)f(t)的的参数是tt
-
-
函数性态(一定要向微积分拓展,使用微积分工具进行研究)
-
单调性
f′(x)>0f′(x)>0与f(x)f(x)单调增的关系:
- 若f′(x)>0f′(x)>0,则f(x)f(x)单调增
- 若f(x)f(x)单调增,则f′(x)>=0f′(x)>=0
反例:f(x)=x3,f′(x)=3x2f(x)=x3,f′(x)=3x2,显然f(x)f(x)此时单调增,但f′(0)=0f′(0)=0
原因:f(x)−f(x0)=O(x−x0)f(x)−f(x0)=O(x−x0),即应变量f(x)f(x)的增长率远小于自变量x的增长率
-
奇偶性
- 连续(f(x)f(x)至少有一个原函数F(x)=∫xaf(x)dtF(x)=∫xaf(x)dt,他的所有原函数是该原函数加常数)的偶函数其原函数不一定是奇函数,因为奇函数的零点值必须为0 => 连续的偶函数其原函数有且只有一个原函数为奇函数
- 奇偶性与单调性:
- 奇函数:左右两侧单调性相同
- 偶函数:左右两侧单调性相反
-
周期性
-
函数是周期函数则导函数一定是周期函数
-
原函数是周期函数当且仅当∫T0f(x)dt=0∫T0f(x)dt=0
证明:
-
正推:定义 => F(x)=F(x+T)F(x)=F(x+T),故∫xaf(x)dt=∫x+Taf(x)dt=∫xaf(x)dt+∫x+Txf(x)dt∫xaf(x)dt=∫x+Taf(x)dt=∫xaf(x)dt+∫x+Txf(x)dt,从而当且仅当∫x+Txf(x)dt=∫T0f(x)dt=0∫x+Txf(x)dt=∫T0f(x)dt=0时成立
-
反推:已知f(x)f(x)是周期函数,∫T0f(x)dt=0∫T0f(x)dt=0,证F(x)=∫x0f(t)dt+CF(x)=∫x0f(t)dt+C为周期函数
由于F(x)=∫x0f(t+T)dt+C=∫x+TTf(t)dt+C=−∫T0f(t)dt+∫x+T0f(t)dt+C=−∫T0f(t)dt+F(x+T)=F(x+T)F(x)=∫x0f(t+T)dt+C=∫x+TTf(t)dt+C=−∫T0f(t)dt+∫x+T0f(t)dt+C=−∫T0f(t)dt+F(x+T)=F(x+T)
-
直观理解:原函数是周期函数,则其递增与递减对等,故其导数在周期内的积分为0
-
-
-
有界性
-
f′(x)f′(x)在区间(非无穷)有界 => f(x)f(x)在区间有界
证明:使用Lagrange定理证明
-
f(x)f(x)在区间有界 无法推出 f′(x)f′(x)可能无界(不存在)
反例:0<=x0<=x,f(x)=√xf(x)=√x,f′(x)=limx→0+√x−0x−0=∞f′(x)=limx→0+√x−0x−0=∞
-
-
-
线性变换与非线性变换
- 线性变换
- 定义:令t=kx+b
- 特点:不会改变图像的基本形式
- k会对图像伸缩
- b会对图像平移
- 非线性变换
- 定义:令t=g(x)
- 特点:会改变图形的基本形式,如拐点,极值点等
- 线性变换
极限
-
极限的概念
-
数列极限
定义:limn−>∞an=Alimn−>∞an=A
几何意义:当n→+∞n→+∞,可以有无数个点落在A的ϵϵ邻域内
-
函数极限
定义:
-
limx→+∞f(x)=Alimx→+∞f(x)=A(仅这个形式下与数列极限相同)
-
limx→−∞f(x)=Alimx→−∞f(x)=A
-
limx→∞f(x)=Alimx→∞f(x)=A
-
limx→+x0f(x)=Alimx→+x0f(x)=A
-
limx→−x0f(x)=Alimx→−x0f(x)=A
-
limx→x0f(x)=Alimx→x0f(x)=A
当x→x0x→x0,x可以不能等于x0x0:
- 原因:limx→x0f(x)=Alimx→x0f(x)=A表达的是一个趋向但不等于的过程,而f(x)=Af(x)=A表达的是一个直接的映射
- 影响:limx→0sinxx=0limx→0sinxx=0,limx→0x∗sin1x=0limx→0x∗sin1x=0,但limx→0sin(x∗sin1x)x∗sin1xlimx→0sin(x∗sin1x)x∗sin1x不存在,因为相对于前者,xx的定义域为不包含0的去心邻域,x∗sin1xx∗sin1x的定义域为包含0的邻域(如x=1nπx=1nπ),此时1x∗sin1x=101x∗sin1x=10无意义
- 总结:要想让等式成立,还需保证内层复合的函数在x取向0的过程中不为0
两个常见的极限
-
limx→0sinxx=1limx→0sinxx=1
证明
- 由不等式sinx<=x<=tanxsinx<=x<=tanx,有1<=xsinx<=cosx1<=xsinx<=cosx,且limx→0cosx=1limx→0cosx=1
- 故由夹逼定理可知,limx→0xsinx=1limx→0xsinx=1
-
limx→0(1+x)1x=elimx→0(1+x)1x=e
-
-
-
极限的性质
-
局部有界性
-
局部保号性
-
A>0A>0 => f(x)>0f(x)>0
使用:先去掉极限号,然后判断正负号
例:limx→0f″(x)\absx=1limx→0f′′(x)\absx=1
故有在x=0x=0的去心邻域内,f″(x)\absx>0f′′(x)\absx>0
即f″(x)>0f′′(x)>0
-
f(x)>=0f(x)>=0 => A>=0A>=0
原因:A是一个点位,f(x)是围绕A的一个偏差极小的过程
-
-
极限与无穷小的关系
-
limn→∞an=alimn→∞an=a,则limn→∞\absan=\absalimn→∞\absan=\absa
证明:由于数列和函数是部分与整体的关系,故可以通过函数间接证明数列
-
当limx→∞f(x)=Alimx→∞f(x)=A:∀X>0,∃ϵ>0,当\absx>X,总是有\absf(x)−A<ϵ∀X>0,∃ϵ>0,当\absx>X,总是有\absf(x)−A<ϵ
由于\abs\absf(x)−\absA<=|f(x)−A|<ϵ\abs\absf(x)−\absA<=|f(x)−A|<ϵ,故limx→∞\absf(x)=\absAlimx→∞\absf(x)=\absA
-
当limx→x0f(x)=Alimx→x0f(x)=A:∀δ>0,∃ϵ>0,当0<\absx−x0<δ,总是有\absf(x)−A<ϵ∀δ>0,∃ϵ>0,当0<\absx−x0<δ,总是有\absf(x)−A<ϵ
注:这里要求0<\absx−x0<δ0<\absx−x0<δ是由极限的过程性所决定的
由于\abs\absf(x)−\absA<=|f(x)−A|<ϵ\abs\absf(x)−\absA<=|f(x)−A|<ϵ,故limx→x0\absf(x)=\absAlimx→x0\absf(x)=\absA
-
综上:原命题成立
-
-
-
极限的存在准则
- 夹逼准则
- 单调有界准则
-
无穷小
-
等价无穷小的数学定义:limf(x)g(x)=1limf(x)g(x)=1
-
等价无穷小的阶数
-
f(x)为n阶等价无穷小:f(x)f(x)~xnxn
-
估阶
- 积分极限下的等价无穷小替换
-
-
公式:αα为n阶等价无穷小,ββ为m阶等价无穷小,则lim∫α0βdxlim∫α0βdx的阶数为(m+1)∗n(m+1)∗n
-
一定为无穷小的情况
-
limαβ=Alimαβ=A
- β→0,A=0β→0,A=0,则limα=0limα=0
-
α→0,A≠0,α→0,A≠0,则limβ=0limβ=0
-
lim(αβ)=A,α→∞lim(αβ)=A,α→∞,则limβ→0limβ→0
-
-
-
无界变量与无穷大量的关系
无界:
- 无穷
- 周期:如an=1,2,1,4,...an=1,2,1,4,...
-
题型
-
极限的概念性质及存在准则
-
求极限
-
确定极限式中的参数
-
通常由函数极限与分子,分母极限的关系确定:分子分母中通常会有一个趋向0
-
尝试直接构造所求的对象
例:已知函数f(x)在x=0的某邻域内可导,且limx→0(sinxx2+f(x)x)=2limx→0(sinxx2+f(x)x)=2,试求f(0),f'(0)及limx→0xf(x)+exlimx→0xf(x)+ex
为了构造f(0)f(0),对分子分母同乘x,可得等式limx→0(sinxx+f(x))=2∗x=0limx→0(sinxx+f(x))=2∗x=0,故f(0)=−1f(0)=−1
-
-
无穷小量阶的比较
-
连续与间断点
-
间断点
-
第一类间断点:左右极限均存在
- 可去间断点
- 跳跃间断点
-
第二类间断点:左右极限至少有一个不存在(无穷间断点,震荡间断点)
-
如何找间断点
f(x)={x\absx+1ln\absx,x≠01,x=0f(x)={x\absx+1ln\absx,x≠01,x=0- 分段函数至少有一个可疑的间断点
- 绝对值函数一般有正负两个可疑的间断点
- 考察基本初等函数及复合函数的定义域
-
-
连续函数的性质
-
基本初等函数在定义域内连续
-
初等函数在定义区间内连续
例:如√sinx−1√sinx−1的定义域就是离散点的点,而不是区间,故不连续
-
闭区间上连续函数的性质
- 有界
- 最值
- 介值(能取到首尾值两端任意) => 推论(能取到最小最大值两端任意)
- 零点定理:首尾异号 => 存在零点
-
-
题型
-
讨论连续性及间断点类型
一个间断点集合可能包含多个间断点类型
例:f(x)=xarctan(1x−1)sin(π2x)f(x)=xarctan(1x−1)sin(π2x)
显然,对分母而言x=2k,k=0,±1,...x=2k,k=0,±1,...都是间断点,但是x=0x=0为第一类间断点中的可去间断点,其它的为第二类间断点中的无穷间断点
-
介值定理
例:证f(ξ)=t1f(x1)+t2f(x2)+...+tnf(xn)f(ξ)=t1f(x1)+t2f(x2)+...+tnf(xn),且ti>0,∑ni=1ti=1ti>0,∑ni=1ti=1
证:通过∑ni=1=1∑ni=1=1,对f(xi)f(xi)整体做上下界的证明
-
零点定理:证明存在某个点,且多需要构造辅助函数
-
难题
- 设f(x)f(x)在[0,1]连续,f(0)=f(1)f(0)=f(1),求证:∃ξ∈[0,1]∃ξ∈[0,1],使f(ξ+14)=f(ξ)f(ξ+14)=f(ξ)
- 设f(x)f(x)在(−∞,+∞)(−∞,+∞)上连续,且limx→∞f(x)x=0limx→∞f(x)x=0,试证存在ξ∈(−∞,+∞)ξ∈(−∞,+∞),使f(ξ)+ξ=0f(ξ)+ξ=0成立
-
二、一元函数微分学
以f(x)=x2f(x)=x2为例理解极限与导数
假设这个函数比较复杂,显然我们无法直接知道f(x)f(x)是如何变化的,如果我们知道当x相对x0x0发生变化时f(x)f(x)的相对变化f(x)−f(x0)x−x0f(x)−f(x0)x−x0,当把这些相对变化连在一起就是整个函数的变化了(类似通过连续的速度变化推路程的变化)。显然我们希望x总是相对x0x0近一点,那么就需要用到极限工具,也就是f′(x0)=limx−>x0f(x)−f(x0)x−x0f′(x0)=limx−>x0f(x)−f(x0)x−x0(这里有一个重要的前提:(从等式右边的极限去理解)x→x0x→x0的含义是左右极限存在且相等(导数存在的冲要条件),否则若不相等则极限究竟算是趋向哪里呢——实际上这算是一个左右极限均存在的第一类间断点中的跳跃间断点 => (从等式左边的导数去理解)故单点可导的定义是左右导数存在且相等)。当我们将x0x0一般化,也就获得了f(x)f(x)的导数f′(x)f′(x)(前提:函数上的每一个点都能求得导数)。
导数与微分
-
导数的概念
-
可导与连导:
-
定义:
- 单点可导:f′(x0)=limx→x0f(x)−f(x0)x−x0f′(x0)=limx→x0f(x)−f(x0)x−x0
- 连续可导:将单点可导中的x一般化即可得到导数公式
-
可导与连续可导的关系:连续可导即处处可导
反例:f(x)=x2sin(1x),x≠0;0,x=0;f(x)=x2sin(1x),x≠0;0,x=0;
可导性证明
- x≠0x≠0:f′(x)=2xsin(1x)−cos(1x)f′(x)=2xsin(1x)−cos(1x)
- x=0x=0:由定义,f′(0)=0f′(0)=0
不连续可导证明:limx→0f′(x)limx→0f′(x)不存在≠≠0
-
-
可导性
-
基本初等函数的可导性:在定义区间处处可导
例:(x12)′=121x12(x12)′=121x12
显然,定义域由[0,∞)→(0,∞)[0,∞)→(0,∞)
-
初等函数的可导性:在定义区间内也不一定处处可导
例:\absx=√x2\absx=√x2
显然,x在x=0x=0处不可导
-
-
-
微分的概念
一元函数微分形式的不变性
对于y=f(u),u=φ(x)=>y=f[φ(x)]y=f(u),u=φ(x)=>y=f[φ(x)],无论对于直接变量(自变量x)还是间接变量(中间变量u)都用相同的微分形式,即:dy=y′xdx=y′uu′xdx=y′ududy=y′xdx=y′uu′xdx=y′udu
-
导数与微分的几何意义
导数为什么是切线的斜率:
-
没有极限的情况下
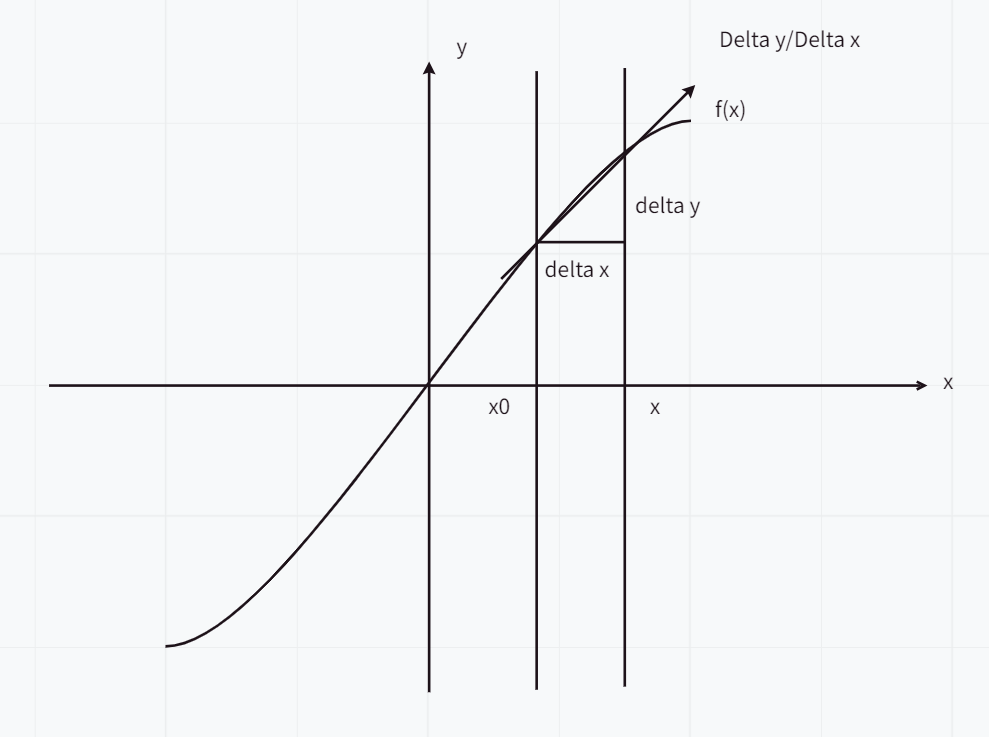
-
有极限的情况下(切线)
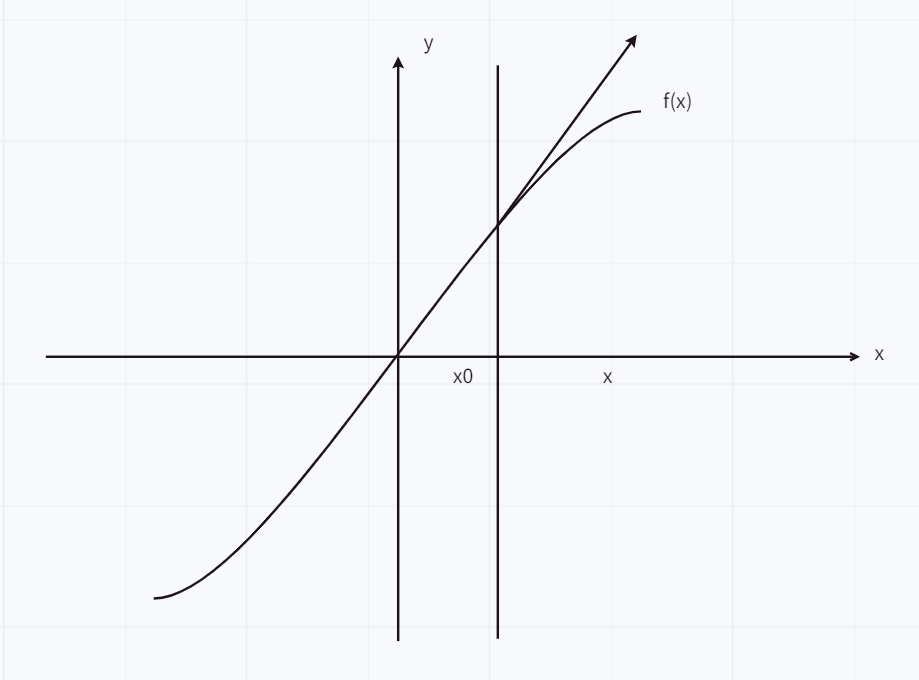
导数与微分的关系:ΔxΔx,ΔyΔy,dx,dy(图片中的delta表示ΔΔ)
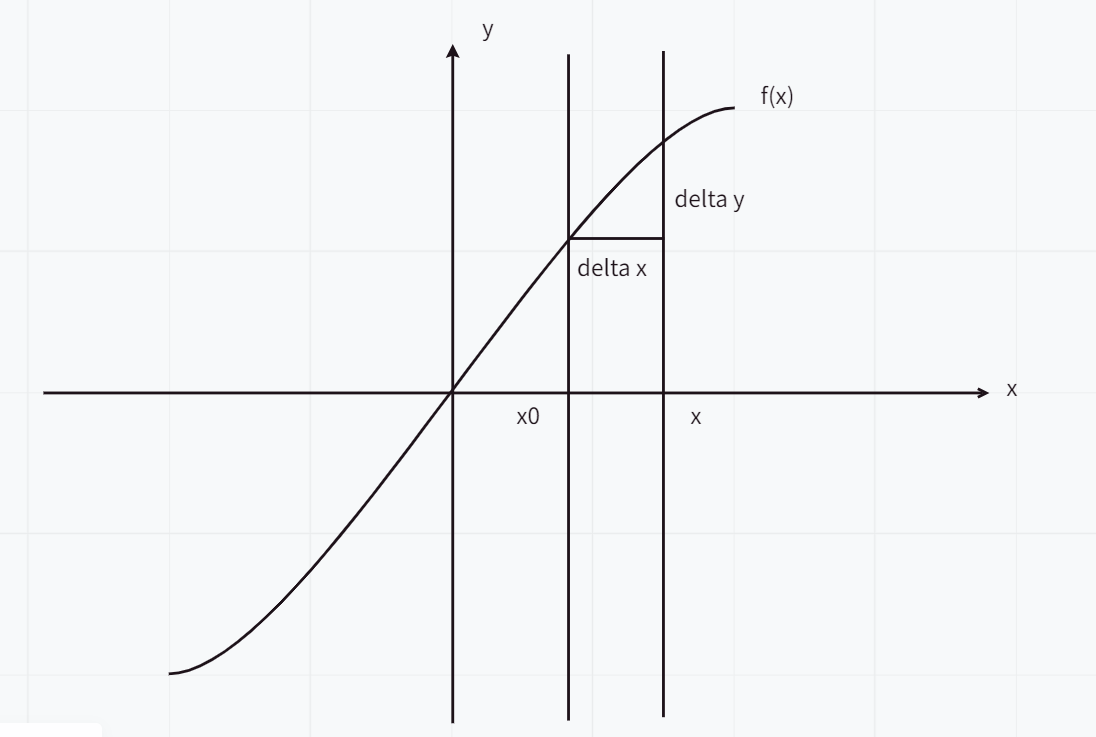
将上面导数定义稍作变形可得f′(x)=limΔx−>0ΔyΔxf′(x)=limΔx−>0ΔyΔx,由无穷小和函数的关系可知ΔyΔx=f′(x)+α(x)ΔyΔx=f′(x)+α(x)(limΔx−>0α(Δx)=0limΔx−>0α(Δx)=0),变形可得Δy=f′(x)Δx+α(x)ΔxΔy=f′(x)Δx+α(x)Δx,有f′(x)f′(x)的几何意义可做切线
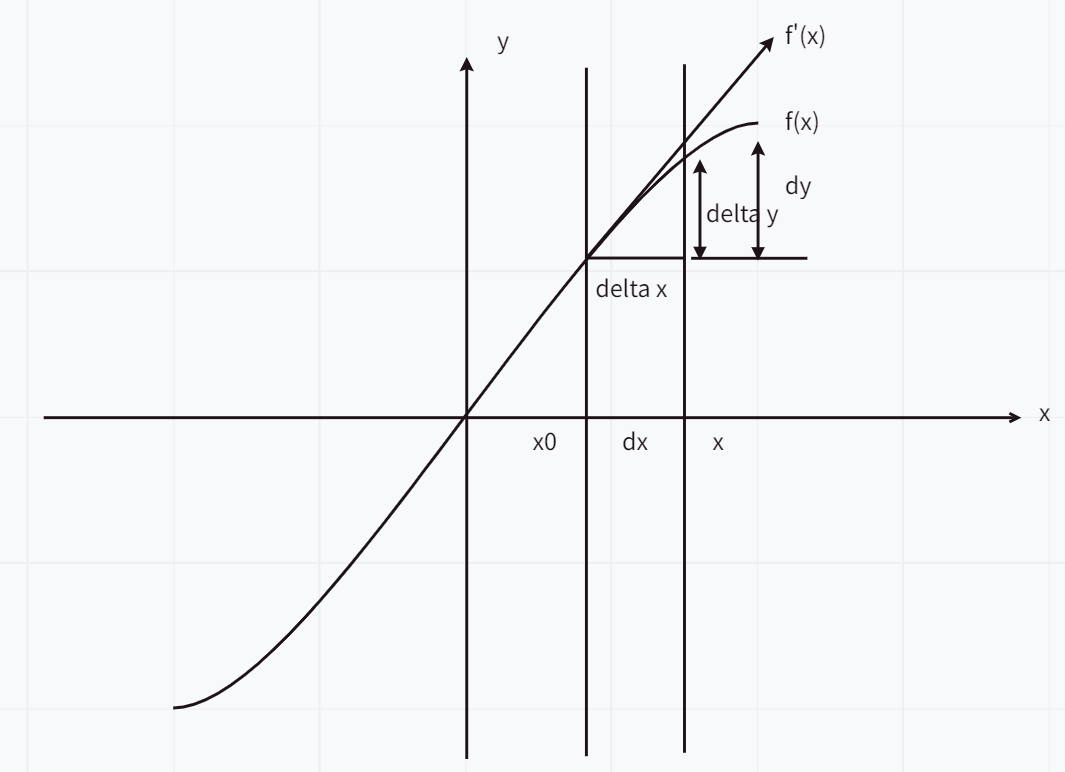
忽略非主线部分的α(x)α(x)即可得Δy≈f′(x)Δx=f′(x)dxΔy≈f′(x)Δx=f′(x)dx,记作。当可以在某点x0x0做这样的近似表达,则称f(x)f(x)在x0x0处可微,称AΔxAΔx为微分dy=f′(x)dxdy=f′(x)dx。
导数的数值意义:若f′(x)=af′(x)=a,则可推得xx每增加一个单位,yy增加AA个单位
注:该思维可以拓展到多元函数微分学的偏导数
-
-
连续,可导,可微之间的关系
- 可导一定连续:由f′(x0)=limx−>x0f(x)−f(x0)x−x0f′(x0)=limx−>x0f(x)−f(x0)x−x0存在且x−x0=0x−x0=0(这里的x0x0可以一般化为函数f(x)f(x)上任意一点,x是趋向于x0x0的左右两侧任意一点),要想让该0000型极限存在,显然f(x)f(x)在x−>x0x−>x0的过程中趋向于f(x0)f(x0),故f(x)在x0x0点连续
- 连续不一定可导:以常见的分段函数f(x)=\absxf(x)=\absx为例,当我们求0点的导数时,其左右导数不相等,故我们无法使用该导数工具求解
- 导数与微分的关系:显然,当且仅当f′(x)f′(x)存在,该表达式才存在。故可导的充分必要条件为可微
-
可导与连续可导
- 可导/导数存在:若f′−(x0)=f′+(x0)f′−(x0)=f′+(x0),则有f′(x0)=f′−(x0)=f′+(x0)f′(x0)=f′−(x0)=f′+(x0)
- 导数连续:f′(x0)=f′(−x0)=f′(+x0)f′(x0)=f′(−x0)=f′(+x0)
注:f′−(x)f′−(x)表示左导数,f′(−x)f′(−x)表示导数的左极限
-
求导公式
-
求导法则
-
有理运算:
-
(u±v)′=u′±v′(u±v)′=u′±v′
-
(uv)′=uv′+u′v(uv)′=uv′+u′v
推导:通过以e为底将乘除转化为±±,uv=elnu+lnvuv=elnu+lnv,故(uv)′(uv)′=uv∗(u′u+v′v)uv∗(u′u+v′v)=u′v+uv′u′v+uv′
使用:对于多个连乘,当我们希望只关注其中一个项时,可以将其它项看做一个整体
例:f(x)=(ex−1)(e2x−2)...(enx−n)f(x)=(ex−1)(e2x−2)...(enx−n)
通过令g(x)=(e2x−2)...(enx−n)g(x)=(e2x−2)...(enx−n),可以观察到f′(x)=g(x)+(ex−1)g′(x)f′(x)=g(x)+(ex−1)g′(x),且f'(0)的右侧式为0
-
(uv)′(uv)′=u′v−uv′v2u′v−uv′v2
推导:uv=elnu−lnvuv=elnu−lnv,故(uv)′(uv)′=uv(u′u−v′v)uv(u′u−v′v)=u′v−uv′v2u′v−uv′v2
-
-
复合函数求导
-
隐函数求导/隐函数存在性定理:dydx=−FxFydydx=−FxFy
注:该公式实际上将一元函数的导数和多元函数偏导数联系在了一起
-
反函数求导:f′(x)=1φ′(y)f′(x)=1φ′(y)
-
参数方程求导:y=ψ(t),x=φ(t)y=ψ(t),x=φ(t)
- 一阶:dydx=ψ′(t)φ′(t)dydx=ψ′(t)φ′(t)
- 二阶:d2ydx2d2ydx2=ddt(ψ′(t)φ′(t))∗1φ′(t)ddt(ψ′(t)φ′(t))∗1φ′(t)
-
对数求导法
-
高阶导数公式
- (sinx)(n)(sinx)(n)=sin(x+n∗π2)sin(x+n∗π2)
- (cosx)(n)(cosx)(n)=sin(x+n∗π2)sin(x+n∗π2)
- (u±v)(n)(u±v)(n)=u(n)±v(n)u(n)±v(n)
- (uv)(n)(uv)(n)=∑nk=0Cknu(k)v(n−k)∑nk=0Cknu(k)v(n−k)
-
-
题型
-
导数的概念
-
导数定义求极限
-
计算
若f(x)f(x)二阶可导,所求极限的分母包含f(x)f(x),分子包含x2x2,如:limf(x)−f(x0)−f′(x0)x2limf(x)−f(x0)−f′(x0)x2
则:
- 通过洛必达:对分子降幂
- 通过导数定义:求二阶导数
注:实际上若f′(x0)=0f′(x0)=0,由Taylor展开可得,结果为f″(x0)2f′′(x0)2
-
利用导数定义求函数自变量
例:已知f′(0)≠0,f(θx)=xf′(0)≠0,f(θx)=x,求limx→0+θlimx→0+θ
通过导数定义将θθ向f(x)f(x)转化
limx→0+f(θx)θxθ=1limx→0+f(θx)θxθ=1
故有limx→0+θ=1f(0)limx→0+θ=1f(0)
-
-
导数定义求导数
某点可导的充分条件是导数存在且连续:f′+(x0)=f′−(x0)=f′(x0)f′+(x0)=f′−(x0)=f′(x0)
含义
-
导数是存在
-
且这种存在是双侧:
例:limx→x0f(x2)−f(x0)x2limx→x0f(x2)−f(x0)x2实际上只代表了单侧x→x0x→x0的导数
-
-
导数定义判断函数的可导性
-
基本方法:求函数表达式,用导数存在的充分必要条件判断间断点左右导数
设函数f(x)=limn√1+\absx3nf(x)=limn√1+\absx3n,则f(x)f(x)在(−∞,+∞)(−∞,+∞)的不可导点个数
-
求函数表达式
f(x)={1,\absx<=1\absx3,\absx>1f(x)={1,\absx<=1\absx3,\absx>1
-
判断间断点的左右导数:实际上由于是偶函数,只需判断一端
-
-
使用与极限相关的可导性定义判定(该题目的内容本质上同上,但因题型第一眼看上去比较新颖故保留,可在适当时间删去)
例:设f(0)=0f(0)=0,则f(x)f(x)在点x=0x=0可导的充要条件为
-
lim1h2f(1−cosh)lim1h2f(1−cosh)存在
错误:由于cosh<1cosh<1,故只满足一侧导数存在
-
lim1hf(1−eh)lim1hf(1−eh)存在
正确
-
lim1h2f(h−sinh)lim1h2f(h−sinh)存在
错误:由于c=a+bc=a+b,当c存在无法推得a,b均存在
-
lim1h[f(2h)−f(h)]lim1h[f(2h)−f(h)]存在
错误:无法由两个动点推得,举反例当x≠0,f(x)=xx≠0,f(x)=x;当x=0,f(x)=1x=0,f(x)=1,显然极限存在且为1,但是函数在x=0x=0处不连续,f(0)f(0)不可导
注:本质上还是理解定义中所给的可导的充要条件。以本题为例应该看到不是f(x)f(x)在点x=0x=0可导的充要条件,而仅仅应该是可导的充要条件
-
-
f(x)=φ(x)\absx−af(x)=φ(x)\absx−a,φ(x)φ(x)在x=ax=a处连续,则f(x)f(x)在x=ax=a处可导的充要条件是φ(a)=0φ(a)=0
注:
- f(x)=xn\absxf(x)=xn\absx是n阶可导
- f(x)f(x)可导与\absf(x)\absf(x)可导的关系
- 当f(x)f(x)不一定连续:既不充分也不必要
- 充分性反例:f(x)=xf(x)=x
- 必要性反例:f(x)={−1,x<=0\1,0<xf(x)={−1,x<=0\1,0<x
- 当f(x)f(x)连续
- 当f(a)≠0f(a)≠0:充分必要
- 当f(a)=0f(a)=0
- 当f′(a)=0f′(a)=0:充分必要
- 当f′(a)≠0f′(a)≠0:\absf(x)\absf(x)导数不存在
- 当f(x)f(x)不一定连续:既不充分也不必要
-
-
-
导数的几何意义
-
导数与微分的计算
-
函数求导分析
-
具体函数:具体分析
-
抽象函数
-
无表达式:
- 看题目中几阶连续可导
- 看题目中几阶可导:则有n-1阶连续可导
-
有表达式(微分方程形式):转换为最高阶导数的表达式,向上判断是否能求导
例:f″(x)+[f′(x)]2=sinxf′′(x)+[f′(x)]2=sinx
转换为最高阶导数的表达式(二阶):f″(x)=sinx−[f′(x)]2f′′(x)=sinx−[f′(x)]2
故f(x)f(x)三阶连续可导
-
-
-
分段函数
- 先用导数定义求间断点的导数:直接决定了导函数的连续性
- 求各分段的导函数
-
复合函数
-
链导法:适用于内外层导数分别可求的情况
反例:
内层函数:g(x)={−√x,x>0x2,x<=0g(x)={−√x,x>0x2,x<=0
外层函数:f(x)={x2,x>=0x4,x<0f(x)={x2,x>=0x4,x<0
复合函数:F(x)=f(g(x))={x2,x>0x4,x<=0F(x)=f(g(x))={x2,x>0x4,x<=0
使用链导法,内层函数g′+(0)=−√xx=∞g′+(0)=−√xx=∞,导数看似不存在
但由复合函数的导数定义可知,f(g(0))=0f(g(0))=0
综上:当内层导数存在,外层导数存在,则复合导数存在,即有F′(0)=f′(g(0))∗g′(0)F′(0)=f′(g(0))∗g′(0);然而当内层导数不存在时,但复合可能会导致函数的阶数变化(在本例中由1212阶变为了2阶),即两者无关
-
导数定义:适合用于具体函数,不适合有抽象函数
例:设φ(x)={x3sin1x,x≠00,x=0φ(x)={x3sin1x,x≠00,x=0,函数f(x)可导,求F(x)=f[φ(x)]F(x)=f[φ(x)]的导数
使用链导法可知F′(0)=f′(0)∗0=0F′(0)=f′(0)∗0=0
使用导数定义可知F′(0)F′(0)=limf(x3sin1x)−f(0)xlimf(x3sin1x)−f(0)x=limf(x3sin1x)−f(0)x3sin1x∗x3sin1xxlimf(x3sin1x)−f(0)x3sin1x∗x3sin1xx=f′(0)∗0f′(0)∗0=00
注:看起来由于左侧极限存在,右侧极限x3sin1x=0x3sin1x=0结果是对的,但实际上由导数定义f′(x)=lim◻→0f(x0+◻)−f(x0)◻f′(x)=lim□→0f(x0+□)−f(x0)□,显然由于极限表示的一种趋向的过程,故◻≠0□≠0。而在本例中,在x→0x→0的过程中,当x=1nπx=1nπ,x3sin1x=0x3sin1x=0,故无法使用导数定义,左侧极限limf(x3sin1x)−f(0)x3sin1x≠f′(0)limf(x3sin1x)−f(0)x3sin1x≠f′(0)且可能不存在,无法使用乘法法则分别求解
-
-
隐函数
-
利用原方程化简:说白了,对于求导后方程来说多了一对可以使用的关系
例:y=tan(x+y)y=tan(x+y),求y′y′,y″y′′
y′=sec2(x+y)∗(1+y′)y′=sec2(x+y)∗(1+y′)
带入y=tan(x+y)y=tan(x+y),可得y′=(1+y2)∗(1+y′)y′=(1+y2)∗(1+y′)
-
-
参数方程
dydx=y′x′dydx=y′x′
-
直接法:
d2ydx2=dy′x′dt∗1x′d2ydx2=dy′x′dt∗1x′
注:这个1x′1x′是最容易漏下的
-
公式法:适合用于具体点
d2ydx2=ddydxdx=y″x′−y′x″x′2∗1x′=y″x′−y′x″x′3d2ydx2=ddydxdx=y′′x′−y′x′′x′2∗1x′=y′′x′−y′x′′x′3
求某点的导数:
-
-
反函数
函数y=f(x)y=f(x)的反函数为x=φ(y)x=φ(y)
则由反函数一阶导数的基本结论:φ′(y)=1y′(x)φ′(y)=1y′(x)
-
直接法
-
公式法
φ″(y)=0−y″(x)y′3(x)φ′′(y)=0−y′′(x)y′3(x)
注:反函数二阶导可以看做参数方程求导的特例,因为dxdx=1,d2xdx2=0dxdx=1,d2xdx2=0
-
-
补充
-
对数求导法:两边取对数,而不是以e为底
-
幂指函数形式:如y=(1+x2)sinxy=(1+x2)sinx
-
乘除形式:如y=3√(x+1)(x+2)x(1+x2)y=3√(x+1)(x+2)x(1+x2)
注:为保证结果为证需要两边加绝对值ln\absyln\absy
-
-
高阶导数
-
公式法
-
乘法:(uv)(n)=∑nk=0Cknu(k)v(n−k)(uv)(n)=∑nk=0Cknu(k)v(n−k)
保零因子
例:对f(x)=(x−1)(x−2)2(x−3)3xf(x)=(x−1)(x−2)2(x−3)3x,求f″(2)f′′(2)
注意到(x−2)|x=2=0(x−2)|x=2=0,则令u(x)=(x−2)2,v(x)=(x−1)(x−3)3u(x)=(x−2)2,v(x)=(x−1)(x−3)3
则有xf(x)=u(x)v(x)xf(x)=u(x)v(x),其中u(x)u(x)称为保零因子
-
三角函数:sin(n)x=sin(x+nπ2)sin(n)x=sin(x+nπ2)
-
-
归纳法
-
多项式:如f(x)=1ax+bf(x)=1ax+b
-
三角函数
-
结合两角和差公式:如f(x)=exsinxf(x)=exsinx => 求导归纳可得f′(x)=√2exsin(x+π4)f′(x)=√2exsin(x+π4)
-
结合降幂公式(也就是倍角公式):如f(x)=sin4x+cos4xf(x)=sin4x+cos4x
直接化简得:f(x)=1−2sin2xcos2x=1−12sin22xf(x)=1−2sin2xcos2x=1−12sin22x
求一阶导降幂得:f′(x)=−2sin2xcos2x=−sin4xf′(x)=−2sin2xcos2x=−sin4x
-
-
-
Taylor级数:f(x)=∑∞n=0f(n)(x0)n!(x−x0)nf(x)=∑∞n=0f(n)(x0)n!(x−x0)n
注:重点在于凑多项式(x−x0)n(x−x0)n
-
-
-
-
导数的应用
将导数作为工具研究函数,具体来说是用微分中值定理研究函数的极值和最值,拐点和凹凸性,渐近线等特性
导数于极值,凹凸性的关系
- 极值与一阶导数:
- 极大值前半段单增:一阶导数由正变负
- 极小值前半段单减:一阶导数由负变正
- 凹凸性与二阶导数
- 凸函数对应极大值:一阶导数由正变负 => 二阶导数<0
- 凹函数对应极小值:一阶导数由负变正 => 二阶导数>0
-
微分中值定理
条件:闭区间连续,开区间可导
-
罗尔定理:f(a)=f(b)f(a)=f(b) => f′(δ)=0f′(δ)=0
几何含义:若左右端点相同,则内部至少有一点为极值点
-
Lagrange定理:f(b)−f(a)=(b−a)f′(δ)f(b)−f(a)=(b−a)f′(δ)
-
柯西定理:f(b)−f(a)g(b)−g(a)=f′(δ)g′(δ)f(b)−f(a)g(b)−g(a)=f′(δ)g′(δ)
-
Taylor公式:在x0x0点展开的Taylor公式为f(x)=f(x0)+f′(x0)(x−x0)+f″(x0)2!(x−x0)2+...+f(n)(x0)n!(x−x0)nf(x)=f(x0)+f′(x0)(x−x0)+f′′(x0)2!(x−x0)2+...+f(n)(x0)n!(x−x0)n
-
Lagrange余项:求极限,极值等局部性态
-
皮亚诺余项:求最值,不等式等整体性态
-
注:
-
罗尔定理,Lagrange定理,柯西定理反映的是函数和一阶导数的关系,而Taylor公式反映的是函数和高阶导数的关系
-
使用Taylor展开求多项式的f(n)(x0)f(n)(x0),在多项式中凑(x−x0)n(x−x0)n,对应的系数即为f(n)(x0)n!f(n)(x0)n!
-
在使用时,由于存在ξξ不定,故一般对相应的高阶导数整体做出了限制,如:f″(x)<0f′′(x)<0,从而可以限制f″(ξ)f′′(ξ)的区间
-
-
极值与最值
-
极值点与驻点(一阶导数,第一充分条件)
驻点:导数为0的点
关系:
- 两者无关
- 判断极值点的第一条件:该点左右两侧的导数正负是否有发生变化
- 当导数前半段为正:说明是极大值
- 当导数前半段为负:说明是极小值
-
二阶导数(第二充分条件)
若f′(x0)=0,f″(x)≠0f′(x0)=0,f′′(x)≠0(说明导数左右两侧正负值发生变化)
- f″(x)>0f′′(x)>0,即f′−(x0)<0f′−(x0)<0,说明是极小值
- f″(x)<0f′′(x)<0,即f′−(x0)>0f′−(x0)>0,说明是极大值
- f″(x)=0f′′(x)=0(本质上使用极值判定的第一充分条件)
- 若f″−(x)>0f′′−(x)>0且f″+(x)>0f′′+(x)>0,说明是极小值
- 若f″−(x)<0f′′−(x)<0且f″+(x)<0f′′+(x)<0,说明是极大值
注:这里对一阶导,二阶导和是极大值还是极限值有了比较平滑的过度,很棒
-
高阶导数(第三充分条件)
f′(x0)=f″(x0)=...=f(n−1)(x0)=0f′(x0)=f′′(x0)=...=f(n−1)(x0)=0,但f(n)(x0)≠0f(n)(x0)≠0
- n为偶数,说明是极值点
- n为奇数,说明不是极值点
-
最值:max(极值,端点)
-
-
曲线的凹向和拐点
注:由图像可知,凹凸性必然伴随极值
- f″(x)>0f′′(x)>0:凹函数(对应极小值)
- f″(x)<0f′′(x)<0:凸函数(对应极大值)
拐点:将极值点的条件升高一阶
-
曲线的渐近线
-
水平渐近线:limx→∞f(x)=Alimx→∞f(x)=A(limx→−∞f(x)=Alimx→−∞f(x)=A,或limx→+∞f(x)=Alimx→+∞f(x)=A)
-
垂直渐近线:limx→x0f(x)=∞limx→x0f(x)=∞(limx→x−0f(x)=∞limx→x−0f(x)=∞,或limx→x+0f(x)=∞limx→x+0f(x)=∞)
注:由于垂直渐进线是x=Ax=A,而limlim所求为y的极限,故此时当y→∞y→∞说明有垂直渐进线
-
斜渐近线:limx→∞f(x)x=a,limx→∞f(x)−ax=blimx→∞f(x)x=a,limx→∞f(x)−ax=b
-
-
平面曲线的曲率
-
作用:描述一条点处不同曲线的弯曲程度
-
定义
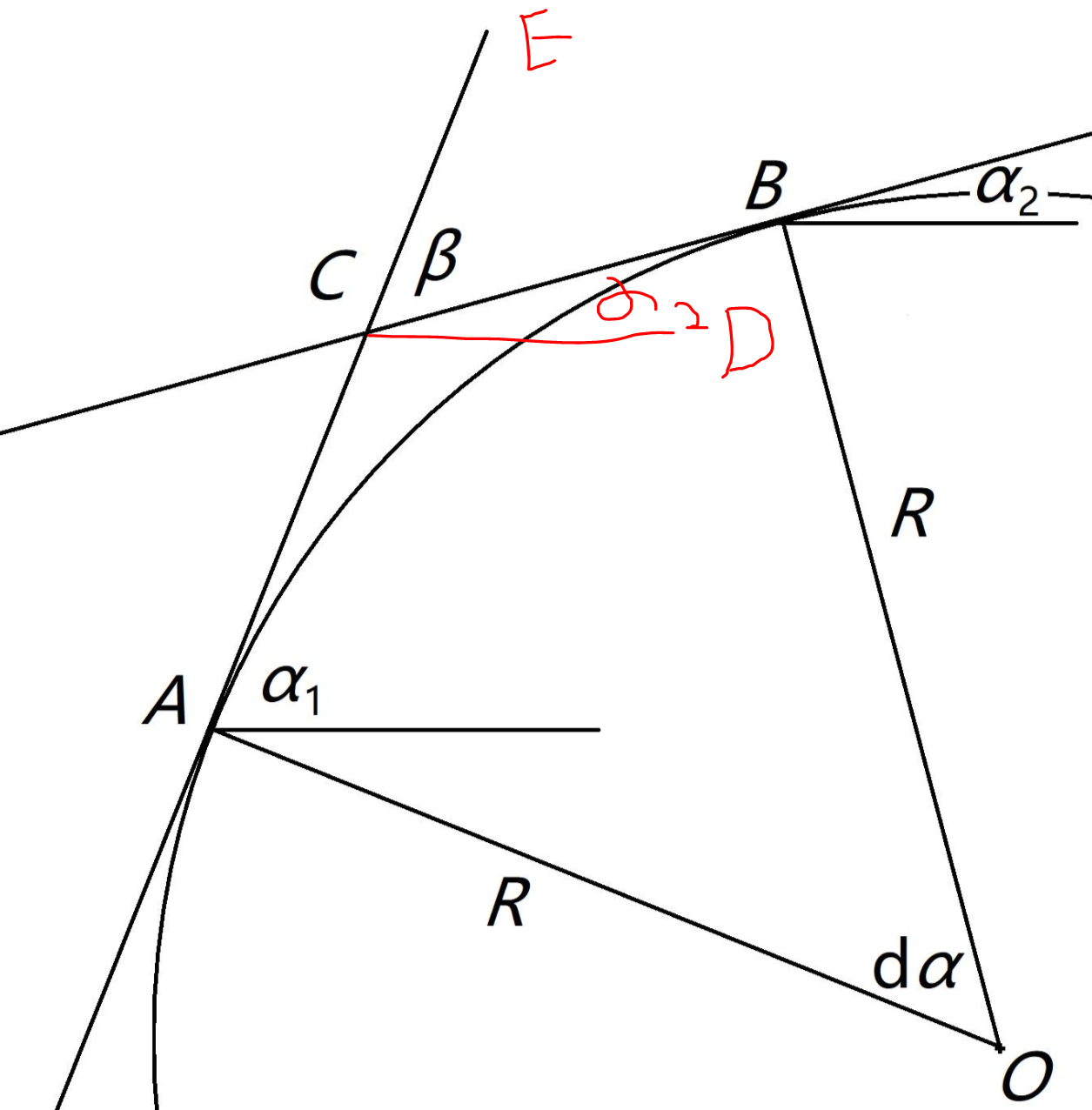
-
由曲率圆的圆弧定义曲率圆
- 曲率圆弧:设A,B为曲线上任意两个无限接近的点,记曲率圆弧ds=ABds=AB
- 曲率圆:记以AB为弧的圆为曲率圆
- 曲率圆心角:记曲率圆弧对应的圆心角为dαdα
- 曲率半径:由弧长公式可知ds=drdαds=drdα,故弧长dr=dsdαdr=dsdα
- 曲率:由于曲率半径越大,曲线的弯曲程度越小,且曲率半径显然只能为正数,故定义曲率KK为曲率半径的倒数的绝对值,即有K=\absdαdsK=\absdαds
-
求曲率
- 求ds:在极限情况下,由勾股定理有ds=√(dx)2+(dy)2ds=√(dx)2+(dy)2,即ds=√1+(dydx)2dx=√1+y′2dxds=√1+(dydx)2dx=√1+y′2dx
- 求dαdα
- 由四边形内角和360度,且OA,OB均为切线,可知dα+<ACB=πdα+<ACB=π,故β=dαβ=dα
- 令α1,α2α1,α2为曲线在A,B点切线的斜率,做平行线CD,即有<ECD=α1,<BCD=α2<ECD=α1,<BCD=α2,故β=α1−α2β=α1−α2
- 又在极限情况下,有dα3=α1−α2dα3=α1−α2,故要求dαdα,只需求dα3dα3
- 由切线的定义有tanα3=y′tanα3=y′,显然α3α3也可以看做对x的函数,故两边对x求导有dα3=y″1+y′2dx=dαdα3=y′′1+y′2dx=dα
- 故K=\absdαds=\absy″(1+y′2)32K=\absdαds=\absy′′(1+y′2)32
注:
- dαdα与dα3dα3的关系
- 在数值上,两者相同
- 在微观几何意义上,前者代表了曲率弧长对应的圆心角,后者代表了切线斜率的增量
- 关于极限情况的解释,由于A,B为两个无限接近的点,故有
- ds=√1+y′2dxds=√1+y′2dx
- dα3=α1−α2dα3=α1−α2
-
-
-
题型
-
函数的单调性,极值和最值
-
单调性:先确定定义域,观察有无奇偶性
-
整个函数无法求导,但已知某一部分恒正或恒负:部分求导
例:设f(x)f(x)在[0,1][0,1]可导,且f(0)=0,0<f′(x)<1f(0)=0,0<f′(x)<1,求证:(∫10f(x)dx)2>∫10f3(x)dx(∫10f(x)dx)2>∫10f3(x)dx
F′(x)=2f(x)∫x0f(t)dt−f3(x)F′(x)=2f(x)∫x0f(t)dt−f3(x)
显然已知f(x)>0f(x)>0,且如果对F′(x)F′(x)整个求导,由于f(x)∫x0f(t)dtf(x)∫x0f(t)dt的存在,无法直接消去∫x0f(t)dt∫x0f(t)dt
故由F′(x)=f(x)[2∫x0f(t)dt−f2(x)]F′(x)=f(x)[2∫x0f(t)dt−f2(x)],只需对
g(x)=2∫x0f(t)dt−f2(x)g(x)=2∫x0f(t)dt−f2(x)求导即可
-
隐函数求极值
-
求驻点:求导后,令y′=0y′=0,最后可能得到的是一个方程,如:y=−2xy=−2x(仅仅是满足y′=0y′=0的解),还需要代回原函数,可能多解,也可能无解
-
判断极值点:一阶导结果非显式形式
-
使用二阶导判断极值更合适
-
当二阶导无法直接求得,可能配合使用极限
例:f(x)f(x)二阶连续可导,且(x−1)f″(x)−2(x−1)f′(x)=1−e1−x(x−1)f′′(x)−2(x−1)f′(x)=1−e1−x,若x=1是极值点,判断是极大值还是极小值
故对f″(x)−2(x−1)f′(x)=1−e1−xx−1f′′(x)−2(x−1)f′(x)=1−e1−xx−1求极限x→1x→1
可得limx→1f″(x)=1limx→1f′′(x)=1
由于f(x)f(x)二阶连续,故limx→1f″(x)=f″(1)=1limx→1f′′(x)=f′′(1)=1
注:这里二阶可导的连续性很重要
-
-
-
阶乘求极值:无法使用导数,故一般用定义法做除法求极值
- 显然当阶乘f(k)!f(k)!中含参数k时,由于f(k)f(k)只能为整数,故k一般也为整数
- 由于阶乘没有导数且阶乘通常使用除法化简,故一般使用定义法:
- 由f(k)!>=f(k−1)!f(k)!>=f(k−1)!,有f(k)!f(k−1)>=1f(k)!f(k−1)>=1
- 同理,有f(k)!f(k+1)>=1f(k)!f(k+1)>=1
- 由上式,即可解得k的范围
注:相关例题见2024概率论辅导讲义,离散型随机变量例3
-
参数方程:参数方程在计算中过程中使用的是t,但在计算结果时需要转换为x,y
-
-
曲线的凹向,拐点,渐近线和曲率
渐近线查找
例:y=ex+1xarctanx2+x+1(x−1)(x−2)y=ex+1xarctanx2+x+1(x−1)(x−2)
-
非垂直渐进线:直接求x→∞x→∞的极限
-
垂直渐近线:同找间断点
注:由于垂直渐近线的y值趋向无穷,故对应无穷间断点,故用找间断点的方法从外层函数向内层函数找间断点即可
求斜渐近线:y=ax+b
-
常规方法
-
a=limx→∞f(x)xa=limx→∞f(x)x
-
b=limx→∞f(x)−axb=limx→∞f(x)−ax
注:若计算ax-f(x)则得到的是-b
-
-
展开为y=ax+b+α(x)(α(x)→0)y=ax+b+α(x)(α(x)→0)形式
具体方法:
Taylor展开
例:y=(1+x)32√x=x(1+1x)32y=(1+x)32√x=x(1+1x)32
-
-
方程根的存在性和个数
-
存在性:
-
零点定理
-
罗尔定理:找原函数及两个相同点
-
微分中值定理(特指非罗尔定理)
例:设f″(x)<0,f(1)=2,f′(1)=−3f′′(x)<0,f(1)=2,f′(1)=−3.求证:f(x)=0f(x)=0在(1,+∞)(1,+∞)有且只有一根
-
Taylor公式:可以基于某一点做高阶展开
由题,有f(x)=f(1)+f′(1)(x−1)+f″(ξ)2(x−1)2f(x)=f(1)+f′(1)(x−1)+f′′(ξ)2(x−1)2,代入得f(x)=2+−3(x−1)+f″(ξ)2(x−1)2f(x)=2+−3(x−1)+f′′(ξ)2(x−1)2
由于f″(x)<0f′′(x)<0,故f(x)<−3x+5f(x)<−3x+5,有f(2)<−1f(2)<−1
注:题目中所给最高是二阶导,故Taylor展开导二阶导即可,本质上讲是从某点的高阶函数展开去看函数整体的变化趋势,会有一定的误差ξξ(对于这一误差,通常我们不需要知道具体的数值,只需要知道正负即可)。
-
Lagrange定理:可以先通过几何分析(导数与原函数的关系)确定要展开的点
由题,通过几何分析,f′(1)=−3f′(1)=−3,即x增长一个单位,f(x)f(x)减小三个单位,故判断f(2)<0f(2)<0
由Lagrange定理,f(2)−f(1)=f′(ξ)f(2)−f(1)=f′(ξ)
又f″(x)<0f′′(x)<0,故f′(x)f′(x)递减,f(2)−f(1)=f′(ξ)<f′(1)=−3<0f(2)−f(1)=f′(ξ)<f′(1)=−3<0
-
-
-
个数:
-
零点唯一:单调性
- F(x)F(x)单调
- F′(x)F′(x)恒正或恒负
-
罗尔定理推论:当x∈[a,b]x∈[a,b],f(n)(x)≠0f(n)(x)≠0,则[a,b][a,b]最多有n个根
证明:反证法,设有n+1个根
例:证明2x−x2=12x−x2=1有且仅有三个实根
下限判断:根据经验划分单调区间,如0,±1,±2,...0,±1,±2,...
上限判断:罗尔定理
-
-
含参
方法:
- 分离参数
- 求值域
- 含参数求导:需要讨论
- 不含参数求导
-
-
证明函数不等式
例:设limx→0f(x)x=1limx→0f(x)x=1,且f″(x)>0f′′(x)>0,证明:f(x)>xf(x)>x
可用微分中值定理,最值,凹凸性
-
单调性
-
由多个参数时,将其中一个参数令为x
例:lnba>2(b−a)b+alnba>2(b−a)b+a
令b为x或a为x(x∈[a,b])(x∈[a,b]),求导
注:
- 本题无f′(x)f′(x)相关结论,故无法使用微分中值定理
- 实际上也可以将a除下来,将baba作为变量
-
幂指函数,通过lnln简化
例:比较eπeπ与πeπe的大小
取对数:πlne,elnππlne,elnπ => 比较lnee,lnππlnee,lnππ
只需求f(x)=lnxxf(x)=lnxx在(e,π)(e,π)的单调性即可
注:幂指函数的单调性与取对数后的单调性相同
-
原函数法:已知抽象函数的不等式,反推原函数的单调性
型如:f(x)>−f′(x)f(x)>−f′(x) => 构造原函数F(x)=exf(x)F(x)=exf(x)
函数构造见微分中值定理有关的证明题
-
-
最值
如:证明f(x)<0(a<x<b)f(x)<0(a<x<b)
除了要证明f(x)f(x)的极大值要小于0,还要证明f(x)f(x)的端点f(a),f(b)f(a),f(b)小于或等于0
-
微分中值定理
- 泰勒公式
- Lagrange定理
注:通过Taylor公式证明得往往也能用Lagrange,因为高阶导数的性态实际上也反映了低阶导数的性态(其关系参见方程根的存在性问题)
-
凹凸性
以凹函数为例,曲线的切线在曲线的下方,即有f(x)>f′(x)f(x)>f′(x)
-
-
微分中值定理有关的证明题
-
证明存在一个点ξ∈(a,b)ξ∈(a,b),使F(ξ,f(ξ),f′(ξ))=0F(ξ,f(ξ),f′(ξ))=0
方法:难点在于找合适的辅助函数,且可能需要补充定义使之连续以满足罗尔定理。构造辅助函数,使用罗尔定理
构造辅助函数:
-
常用公式
-
xf′(x)+nf(x)=0xf′(x)+nf(x)=0 => F(x)=xnf(x)F(x)=xnf(x)
注:重点关注n是怎么来的
-
xf′(x)−nf(x)=0=>F(x)=f(x)xnxf′(x)−nf(x)=0=>F(x)=f(x)xn
-
f′(x)+g(x)f(x)=0f′(x)+g(x)f(x)=0 => F(x)=e∫g(x)dxf(x)F(x)=e∫g(x)dxf(x)
注:上面的是最一般的结论,关键是确定f′(x),f(x)f′(x),f(x)
-
-
还原法(分析法)
-
微分方程法
-
求微分方程F(x,y,y′)=0F(x,y,y′)=0的通解,H(x,y)=CH(x,y)=C
-
设辅助函数:g(x)=H(x,f(x))g(x)=H(x,f(x))
若:g(x)g(x)为ln(...)ln(...)形式,则直接令g(x)=...g(x)=...即可,因为(lng(x))′=g′(x)g(x)(lng(x))′=g′(x)g(x),由于ln的限制g(x)g(x)显然不能为0,求(ln(g(x)))′=0(ln(g(x)))′=0,即求g′(x)=0g′(x)=0
-
注:
-
构造函数的连续性(为满足罗尔定理的使用,需要保证原函数连续——可以为分段函数)
例:设f(x)f(x)在[0,1][0,1]上连续,f(0)=0f(0)=0,∫10f(x)dx=0∫10f(x)dx=0,求证:∃ξ∈(0,1)∃ξ∈(0,1),使∫ξ0f(t)dt=ξf(ξ)∫ξ0f(t)dt=ξf(ξ)
-
结果等式变换:为0=f(ξ)−∫ξ0f(t)dtξ0=f(ξ)−∫ξ0f(t)dtξ,需要注意的是这里天然成立,因为ξξ在开区间
-
构造辅助函数:F(x)=∫x0f(t)dtxF(x)=∫x0f(t)dtx
在这里要注意辅助函数的定义域:因为微分中值定理的使用要保证函数在闭区间连续,而显然当前构造的辅助函数缺少x=0的定义
-
补充定义域:F(0)=limx→0F(x)=0F(0)=limx→0F(x)=0
-
-
辅助函数的选择:由不同方法构造的辅助函数可能不同,不同辅助函数需要代入的点可能不同,可以先通过几何验证可行性(如:对于f(x)=xf(x)=x,当已知f(0)=0,f(1)=1f(0)=0,f(1)=1且f(x)连续,)。
例:设奇函数f(x)f(x)在[-1,1]上具有2阶导数,且f(1)=1f(1)=1
(1).存在ξ∈(0,1)ξ∈(0,1),使得f′(ξ)=1f′(ξ)=1
(2).存在η∈(−1,1)η∈(−1,1),使得f″(η)+f′(η)=1f′′(η)+f′(η)=1
对于题而
-
若用还原法构造辅助函数:F(x)=f′(x)+f(x)−1F(x)=f′(x)+f(x)−1,应代入x=1使用罗尔定理
注:构造辅助函数时f′(x)f′(x)在前
-
若用常用公式构造辅助函数:F(x)=ex(f′(x)−1)F(x)=ex(f′(x)−1),应代入(1)中的ξξ
-
-
-
证明存在两个点ξ,η∈(a,b).ξ,η∈(a,b).使F[ξ,η,f(ξ),f(η),f′(ξ),f′(η)]=0F[ξ,η,f(ξ),f(η),f′(ξ),f′(η)]=0
-
不要求ξ≠ηξ≠η
方法:难点在于找原函数。分离ξ,ηξ,η,找原函数,在同一个区间用两次中值定理(Lagrange,Cauchy等)
-
Lagrange中值定理
-
基本形式
例:(b−a)f′(ξ)(b−a)f′(ξ)
忽略常数,注意到[f(x)]′=f′(x)[f(x)]′=f′(x)
则有f(b)−f(a)f(b)−f(a)=(b−a)f′(ξ)(b−a)f′(ξ)
-
含有f(ξ)f(ξ)形式
例:eξ[f(ξ)+f′(ξ)]eξ[f(ξ)+f′(ξ)]
忽略常数,注意到[exf(x)]′=eξ[f(x)+f′(x)][exf(x)]′=eξ[f(x)+f′(x)]
则有exf(x)b−aexf(x)b−a=eξ[f(ξ)+f′(ξ)]eξ[f(ξ)+f′(ξ)]
-
-
Cauchy中值定理
-
分数形式
例:f′(η)2ηf′(η)2η
忽略常数,注意到f(b)−f(a)b2−a2=f′(η)(b−a)2ηf(b)−f(a)b2−a2=f′(η)(b−a)2η
f(b)−f(a)=b+a2ηf′(η)f(b)−f(a)=b+a2ηf′(η)
-
结论证明:找嫁接桥梁
如(b−a)f′(ξ)(b−a)f′(ξ)=f(b)−f(a)f(b)−f(a)=b+a2ηf′(η)b+a2ηf′(η),其中f(b)−f(a)f(b)−f(a)就是桥梁
-
-
要求ξ≠ηξ≠η
方法:难点在于分位点的选取。反向代入Lagrange中值定理,寻找并证明合适的分位点c
分位点c选取:
-
由第一题获得
-
反证法:同一个等式经过变换
例:设f(x)在[0,1]上连续,在(0,1)内可导,且f(0)=0,f(1)=1,试证对任意给定的正数a,b,在(0,1)内一定存在互不相同的ξ,ηξ,η,使af′(ξ)+bf′(η)=a+baf′(ξ)+bf′(η)=a+b
-
设分界点为c
-
设ξ<ηξ<η,由Lagrange定理可知,f(c)−f(0)=cf′(ξ),f(1)−f(c)=(1−c)f′(η)f(c)−f(0)=cf′(ξ),f(1)−f(c)=(1−c)f′(η)
-
代入结论
-
变换可得:acf(c)+b1−c1−f(c)=a+bacf(c)+b1−c1−f(c)=a+b
观察可得:需证明f(c)=cf(c)=c
由条件f(0)=0,f(1)=1f(0)=0,f(1)=1,画图可知该结论无法证明(y=f(x),y=xy=f(x),y=x可以没有交点)
-
继续变换可得:aa+bcf(c)+ba+b1−c1−f(c)=1aa+bcf(c)+ba+b1−c1−f(c)=1
观察可得:需证明f(c)=aa+bf(c)=aa+b
由条件f(0)=0,f(1)=1f(0)=0,f(1)=1及介值定理可知等式成立
-
类似:
- 对于f(c)c1−f(c)1−c=1f(c)c1−f(c)1−c=1,可以取到两种可能的解
- f(c)=cf(c)=c:太过简单,一般无法证得
- f(c)=1−cf(c)=1−c
-
结论证明:通过等式左侧向右侧证明获得
如:证明f′(ξ)f′(η)=1f′(ξ)f′(η)=1,应将ξ,ηξ,η的Lagrange等式代入,即有f′(ξ)f′(η)=F(c)f′(ξ)f′(η)=F(c),借助c点相关的条件即可证明
注:为什么只能用Lagrange中值定理,因为罗尔定理的结论为f′(ξ)=0f′(ξ)=0,且条件较为苛刻。Cauchy的结论不适合做反向代入,因为有两个函数
-
-
证明存在一个中值点ξ∈(a,b)ξ∈(a,b),使F[ξ,f(n)(ξ)]>=0(n>=2)F[ξ,f(n)(ξ)]>=0(n>=2)
方法:难点在于以怎样的形式向结果转化。使用Lagrange余项的Taylor公式,代入后根据结论向结果转化
-
在哪点展开:根据函数信息。若一样多,优先选导数的,否则可以一起展开
注:一些间接获得函数值和导数值信息的方法
- min0<=x<=1f(x)=−1min0<=x<=1f(x)=−1 => f(c)=−1,f′(c)=0f(c)=−1,f′(c)=0
-
使用哪一个点代入:根据要证明的结论
例:设f(x)f(x)在[a,b][a,b]上二阶可导,f′(a)=f′(b)=0f′(a)=f′(b)=0,求证:∃ξ∈(a,b)∃ξ∈(a,b),使\absf″(ξ)>=4\absf(b)−f(a)(b−a)2\absf′′(ξ)>=4\absf(b)−f(a)(b−a)2
展开点为:
f(x)=f(a)+f′(a)(x−a)+f″(ξ1)2!(x−a)2f(x)=f(a)+f′(a)(x−a)+f′′(ξ1)2!(x−a)2
f(x)=f(b)+f′(b)(x−b)+f″(ξ2)2!(x−b)2f(x)=f(b)+f′(b)(x−b)+f′′(ξ2)2!(x−b)2
显然这里(b−a)24(b−a)24是从(x−a)2,(x−b)2(x−a)2,(x−b)2来的,则可代入x=a+b2x=a+b2
f(a+b2)=f(a)+f′(a)(b−a2)+f″(ξ1)2!(b−a2)2f(a+b2)=f(a)+f′(a)(b−a2)+f′′(ξ1)2!(b−a2)2
f(a+b2)=f(b)+f′(b)(a−b2)+f″(ξ2)2!(a−b2)2f(a+b2)=f(b)+f′(b)(a−b2)+f′′(ξ2)2!(a−b2)2
则有f(b)−f(a)=f″(ξ1)2!(b−a2)2+f″(ξ2)2!(a−b2)2f(b)−f(a)=f′′(ξ1)2!(b−a2)2+f′′(ξ2)2!(a−b2)2,使用不等式向结论转化即可
-
如何向结论转换:由于展开的点,代入得点均可能为多个,故存在由多个ξ1,ξ2,...ξ1,ξ2,...向最终唯一的ξξ转换的问题
-
若结论为f″(ξ)>=8f′′(ξ)>=8这样的直接形式,直接代入得方程做分类讨论
如,当前有
f″(ξ1)=2c2,ξ1∈(0,c)f′′(ξ1)=2c2,ξ1∈(0,c)
f″(ξ2)=2(1−c)2,ξ2∈(c,1)f′′(ξ2)=2(1−c)2,ξ2∈(c,1)
证明f″(ξ)>=8f′′(ξ)>=8
分为(0,c),(c,1)(0,c),(c,1)两个区间讨论
-
若结论为f(b)−f(a)f(b)−f(a)这样的抽象函数形式,显然应该将两个Lagrange公式相加减
-
利用高阶导数的连续性
若相加减后结果为f(a)+f(−a)=a22(f″(ξ1)+f″(ξ2))f(a)+f(−a)=a22(f′′(ξ1)+f′′(ξ2)),而所求结果为f(a)+f(−a)=a2f″(ξ)f(a)+f(−a)=a2f′′(ξ)
寻找f″(ξ1),f″(ξ2),f″(ξ)f′′(ξ1),f′′(ξ2),f′′(ξ)的关系,由f″(x)f′′(x)的连续性及介值定理,显然可取到f″(ξ)=f″(ξ1)+f″(ξ2)2(ξ∈(ξ1,ξ2))f′′(ξ)=f′′(ξ1)+f′′(ξ2)2(ξ∈(ξ1,ξ2))
-
利用不等式
例:f(a)−f(−a)=12[f″(ξ1)(a−x)2−f″(ξ2)(a+x0)2]f(a)−f(−a)=12[f′′(ξ1)(a−x)2−f′′(ξ2)(a+x0)2]
则有
\absf(a)−f(−a)=12\abs[f″(ξ1)(a−x)2−f″(ξ2)(a+x0)2]<=12[\absf″(ξ1)(a−x)2+\absf″(ξ2)(a+x0)2]<=12[\absf″(ξ)\abs(a−x)2+\absf″(ξ)\abs(a+x0)2]<=12\absf″(ξ)[\abs(a−x)2+\abs(a+x0)2](f″(ξ)=max(f″(ξ1),f″(ξ2)))\absf(a)−f(−a)=12\abs[f′′(ξ1)(a−x)2−f′′(ξ2)(a+x0)2]<=12[\absf′′(ξ1)(a−x)2+\absf′′(ξ2)(a+x0)2]<=12[\absf′′(ξ)\abs(a−x)2+\absf′′(ξ)\abs(a+x0)2]<=12\absf′′(ξ)[\abs(a−x)2+\abs(a+x0)2](f′′(ξ)=max(f′′(ξ1),f′′(ξ2)))
使用了绝对值不等式:\abs\absa−\absb<=\absa±b<=\absa+\absb\abs\absa−\absb<=\absa±b<=\absa+\absb
且:\absab=\absa\absb\absab=\absa\absb
细节:二阶导函数连续,二阶导函数的绝对值连续
-
注:若要求证明max0<=x<=1f″(x)>=8max0<=x<=1f′′(x)>=8,即证明f″(ξ)>=8(ξ∈[0,1])f′′(ξ)>=8(ξ∈[0,1])
-
-
-
-
-
三、一元函数积分学
从面积变化的角度去看整个积分学,重点理解原函数,不定积分,定积分,变上限积分几个概念,相互关系,存在性定理。在学习过程中,函数和原函数的关系可以参考导数和函数的关系。
关于原函数与定积分:两者是两个不同的概念,前者是导数定义的逆运用,后者是基于面积的几何定义
存在性:
- 原函数:参照导数定义,当f(x)f(x)连续一定有原函数,有第一类间断点没有原函数(证明见下)
- 定积分:连续一定可积,有限个第一类间断点可积(对积分数值不产生影响)
关于定积分与变上限积分:变上限积分是定积分的子概念
存在性:当f(x)f(x)连续,才有定积分,表现了积分的连续性
关于原函数与变上限积分
当f(x)f(x)连续:f(x)f(x)有原函数,定积分,变上限积分
由于f(x)f(x)连续,故可结合牛顿莱布尼兹公式,由[∫x0f(t)dt]′=[Φ(x)−Φ(a)]′=f(x)[∫x0f(t)dt]′=[Φ(x)−Φ(a)]′=f(x),故变上限积分是f(x)f(x)的一个原函数
证明
- 数学证明是必要的
- 几何证明是直观的
不定积分
-
两个基本概念
- 原函数
- 不定积分:原函数的全体
-
原函数的存在性
-
函数连续一定有原函数
注:
- 变上限积分至少是一个原函数,其它函数可以表示为变上限积分+C
- 函数与原函数的关系(参考导数与函数的关系)
- 函数连续,原函数可导(导数连续,函数可导)
- 有原函数,函数不一定连续(函数可导,导数不一定连续)
-
函数有第一类间断点,则没有原函数
反证法:
不妨设函数为f(x)f(x),原函数为F(x)F(x),原函数的特点是处处可导
则有F′(x)=f(x)F′(x)=f(x)
由于是第一类间断点,有
F′−(x)=f(x)=limx→x−0F(x)−F(x0)x−x0洛必达limx→x0f(x)=f(x0)=AF′−(x)=f(x)=limx→x−0F(x)−F(x0)x−x0洛必达limx→x0f(x)=f(x0)=A
同理,F′+(x)=f(x)=limx→x+0F(x)−F(x0)x−x0=f(x0)=BF′+(x)=f(x)=limx→x+0F(x)−F(x0)x−x0=f(x0)=B
两种情况
-
可去间断点,即有A=BA=B
由导数定义可知,当F′−(x0)=F′+(x0)=AF′−(x0)=F′+(x0)=A,有f(x0)=F′(x0)=Af(x0)=F′(x0)=A,这与f(x)f(x)在x0x0处间断相矛盾
-
跳跃间断点,即有A≠BA≠B
由导数定义可知,F(x)F(x)在x0x0处不可导,这与F(x)F(x)处处可导相矛盾
考虑间断点可导的情况
例:经典的震荡函数F(x)={x2sin1x,x≠00,0F(x)={x2sin1x,x≠00,0
f(x)=F′(x)={xsin1x−cos1x,x≠00,x=0f(x)=F′(x)={xsin1x−cos1x,x≠00,x=0
首先原函数恰好处处可导,其次函数在0点处不连续但
注:
- 函数处处有定义,故原函数处处有定义,即可导(导函数处处有定义,原函数处处可导)
- 无论是连续还是间断,首先都是有定义的
-
-
-
不定积分的性质
-
运算性质
-
(∫f(x)dx)′=f(x)(∫f(x)dx)′=f(x)
-
∫f′(x)dx=f(x)+c∫f′(x)dx=f(x)+c
注意:计算结果是不定积分而不是原函数,故需要加c,这是从概念上的区别
-
-
-
基本积分公式
-
三种主要积分法
-
三类常见可积函数的积分
-
题型
-
计算不定积分
-
不定积分杂例
-
I=∫xf′(x)dx=xf(x)−∫f(x)dxI=∫xf′(x)dx=xf(x)−∫f(x)dx
-
利用抽象函数关系式
- (F2(x))′=2F(x)F′(x)(F2(x))′=2F(x)F′(x)
- (F(x)F′(x))′=F′2(x)+F(x)F″(x)(F(x)F′(x))′=F′2(x)+F(x)F′′(x)
-
f(x)=∫f(x)dx=∫f(u)duf(x)=∫f(x)dx=∫f(u)du
例:由f′(ex)=sinxf′(ex)=sinx,求f(x)f(x)
- 间接求解:将变量代换会
f'(x)形式,再做积分 - 直接求解:∫f′(ex)dex=∫sinxdex∫f′(ex)dex=∫sinxdex
- 间接求解:将变量代换会
-
-
定积分
-
定积分概念
公式:∫baf(x)dx=limλ→0f(ξk)Δxk∫baf(x)dx=limλ→0f(ξk)Δxk
注:
- 定积分是一个和式极限
- 影响定积分结果的因素
- 被积函数f(x)f(x)
- 积分上下限∫ba∫ba
- n等分
- 取左侧:∫10f(x)dx=limn→∞∑ni=1f(i−1n)∫10f(x)dx=limn→∞∑ni=1f(i−1n)
- 取左侧:∫10f(x)dx=limn→∞∑ni=1f(i−1n+in2)=limn→∞∑ni=1f(2i−12n)∫10f(x)dx=limn→∞∑ni=1f(i−1n+in2)=limn→∞∑ni=1f(2i−12n)
- 取右侧:∫10f(x)dx=limn→∞∑ni=1f(in)∫10f(x)dx=limn→∞∑ni=1f(in)
-
定积分几何意义
对于∫baf(x)dx∫baf(x)dx
-
被积函数:设积分上限大于下限
- 当f(x)f(x)恒正:积分为正数(面积)
- 当f(x)f(x)恒负:积分为负数(面积的负数)
- 当f(x)f(x)有正有负:积分可能为正数也可能为负数(正负面积相消)
-
积分上下限:设f(x)f(x)恒正
-
当b>ab>a:积分为正数
-
当b<ab<a:积分为负数
如:2x∫x21e−t2dt2x∫x21e−t2dt,当x∈(−1,1)x∈(−1,1),积分为负数
-
-
-
可积性
-
必要条件:可积一定有界,但有界不一定可积
反例:(狄利克雷函数)D(x)={1,x有理数0,x无理数D(x)={1,x有理数0,x无理数,求∫baD(x)dx∫baD(x)dx
由定积分定义,在分段后需要在每段中采样一个点,而在每一个分段区间中必然包括x的有理数点和无理数点,倘全部取有理数点,则结果显然为b−ab−a;倘若全部取无理数点,则结果显然为0,综上该积分不存在,该函数有界但不可积
-
充分条件:f(x)f(x)在[a,b][a,b]上仅有有限个第一类间断点
-
-
定积分的计算
-
牛莱公式:∫baf(x)dx=F(b)−f(a)∫baf(x)dx=F(b)−f(a)
使用条件:f(x)f(x)连续
弱化条件:f(x)f(x)可积且有原函数
-
换元积分法
-
分部积分法:∫baudv=uv|ba−∫bavdu∫baudv=uv|ba−∫bavdu
-
奇偶性与周期性
- 奇偶性:TODO:把另一部分笔记拿过来
- 周期性:∫α+Tαf(x)dx=∫T0f(x)dx∫α+Tαf(x)dx=∫T0f(x)dx
-
-
变上限积分函数
-
变上限积分的存在性:f(x)f(x)连续 => F(x)=∫xaf(x)dxF(x)=∫xaf(x)dx
-
为什么说变上限积分是一个原函数
以f(x)=x2f(x)=x2为例
∫x0x2dx=13x3∫x0x2dx=13x3
故可知变上限积分是普通函数形式的另一种表达
-
变上限积分函数∫xaf(t)dt∫xaf(t)dt与f(x)f(x)不定积分和f(x)f(x)的关系
-
与原函数
当f(x)f(x)连续,f(x)f(x)有原函数,可积且有变上限积分
故∫f(x)dx=∫xaf(t)dt+c∫f(x)dx=∫xaf(t)dt+c
-
与导数:(∫xaf(t)dt)′=f(x)(∫xaf(t)dt)′=f(x)
微积分基本定理:设f(x)f(x)在[a,b][a,b]上连续,则∫xaf(t)dt∫xaf(t)dt在[a,b][a,b]上可导且(∫xaf(t)dt)′=f(x)(∫xaf(t)dt)′=f(x)
-
-
-
定积分的性质
-
中值定理
-
∫baf(x)dx=f(ξ)(b−a),a<ξ<b∫baf(x)dx=f(ξ)(b−a),a<ξ<b
已知f(x)f(x)的抽象函数表达式,可以尝试估测函数上一点值
例:已知f(x)=g(x)−2x∫10g(x)dxf(x)=g(x)−2x∫10g(x)dx
∫10f(x)dx=∫10g(x)dx−∫10g(x)dx=0∫10f(x)dx=∫10g(x)dx−∫10g(x)dx=0
故由积分中值定理,∃c∈(0,1)∃c∈(0,1),且f(c)=0f(c)=0
-
积分中值定理扩展
若g(x)g(x)不变号,则有∫baf(x)g(x)dx=f(ξ)∫bag(x)dx∫baf(x)g(x)dx=f(ξ)∫bag(x)dx
证明:
令F(x)=∫xaf(x)g(x)dx,G(x)=∫xag(x)dxF(x)=∫xaf(x)g(x)dx,G(x)=∫xag(x)dx
则有F(b)−F(a)G(b)−G(a)=F′(ξ)G′(ξ)=f(ξ)F(b)−F(a)G(b)−G(a)=F′(ξ)G′(ξ)=f(ξ)
故有∫baf(x)g(x)dx=f(ξ)∫bag(x)dx∫baf(x)g(x)dx=f(ξ)∫bag(x)dx
注:没有b−ab−a
-
-
不等式
-
相同积分区间,函数关系不等式对应的积分关系不等式
若f(x)<=g(x)f(x)<=g(x),则有∫baf(x)dx<=∫bag(x)dx∫baf(x)dx<=∫bag(x)dx
-
介值定理
m(b−a)<=∫baf(x)dx=f(ξ)(b−a)<=M(b−a)m(b−a)<=∫baf(x)dx=f(ξ)(b−a)<=M(b−a)
-
绝对值不等式
\abs∫baf(x)dx<=∫ba\absf(x)dx\abs∫baf(x)dx<=∫ba\absf(x)dx
-
-
-
ΓΓ函数
-
定义:Γ(s)=∫+∞0xs−1e−xdx,s>0Γ(s)=∫+∞0xs−1e−xdx,s>0
收敛性证明:
原式=∫10xs−1e−xdx+∫+∞1xs−1e−xdx∫10xs−1e−xdx+∫+∞1xs−1e−xdx
-
左边=∫10xs−1e−xdx∫10xs−1e−xdx
对于x→0x→0,s−1+1>0s−1+1>0,故收敛
-
右边=∫+∞1xs−1e−xdx∫+∞1xs−1e−xdx
对于x→∞x→∞,s−1+1>0s−1+1>0,limx→∞xs−1limx→∞xs−1,但是其速度原小于e−xe−x,故收敛
详细证明
由比较判别法的极限形式,limx→∞xs−1e−x1xmlimx→∞xs−1e−x1xm,且m足够大
但limx→∞xs−1e−x1xm=0limx→∞xs−1e−x1xm=0
而∫∞11xm∫∞11xm收敛,故原积分收敛
-
综上,该积分收敛
-
-
递推公式:
Γ(s+1)=sΓ(s)Γ(s+1)=sΓ(s)
Γ(n+1)=n!(n∈N∗)Γ(n+1)=n!(n∈N∗)
递推公式证明:
-
当s>1s>1,原式
=∫+∞0xs(−1)de−x∫+∞0xs(−1)de−x
=−xse−x|+∞0+∫+∞0sxs−1e−xdx−xse−x|+∞0+∫+∞0sxs−1e−xdx
=sΓ(s)sΓ(s)
-
当s=1s=1,原式=∫+∞0x1−1e−xdx=∫+∞0e−xdx=−e−x|+∞0=1∫+∞0x1−1e−xdx=∫+∞0e−xdx=−e−x|+∞0=1
-
当s=12s=12,原式=∫+∞0x12−1e−xdx=∫+∞0x−12e−xdx∫+∞0x12−1e−xdx=∫+∞0x−12e−xdx
-
换元为偶函数
令x=t2x=t2,即t=x12t=x12,有Γ(12)Γ(12)
=∫∞0t−1e−x22tdt∫∞0t−1e−x22tdt
=∫∞02e−x2dt∫∞02e−x2dt
=∫∞−∞e−x2dt∫∞−∞e−x2dt
-
由正态分布,有上式=∫∞∞e−(√2x)22dx∫∞∞e−(√2x)22dx
=∫∞∞1√2πe−(√2x)22d(√2x)1√2√2π∫∞∞1√2πe−(√2x)22d(√2x)1√2√2π
=√π√π
-
-
综上,Γ(s+1)=∫+∞0xsde−x(−1)=s!Γ(s+1)=∫+∞0xsde−x(−1)=s!
注:记公式主要还是关注x的系数
-
-
-
题型
-
定积分的概念,性质及几何意义
-
求极限
例:f(x)f(x)连续,且limx→+∞f(x)=1limx→+∞f(x)=1,则limx→+∞∫x+2xtsin3tf(t)dtlimx→+∞∫x+2xtsin3tf(t)dt
-
积分中值定理第一性
原式=limx→+∞2(csin3cf(c))=6,c∈(x,x+2)limx→+∞2(csin3cf(c))=6,c∈(x,x+2)
例:求极限limn→∞∫10xn√1+x2dxlimn→∞∫10xn√1+x2dx
-
夹逼准则
注:将limlim代入可以估算极限为0,但不能直接这样做。因为定积分本质上上也是个极限,直接交换两个极限次序的要求是超纲内容
左侧:由于被积函数大于等于0,故该积分大于等于0,该积分的极限大于等于0
右侧:由积分不等式,limn→∞∫10xn√1+x2dx<=limn→∞∫10xn√2dxlimn→∞∫10xn√1+x2dx<=limn→∞∫10xn√2dx
综上,该积分的极限为0
-
积分中值定理第二性
原式=limn→∞√1+c2∫10xndx=√climn→∞11+n=0(c∈(0,1))limn→∞√1+c2∫10xndx=√climn→∞11+n=0(c∈(0,1))
注:
-
为什么不能用积分中值定理第一性
由积分中值定理第一性,原式=limn→∞cn√1+c2,c∈(0,1)limn→∞cn√1+c2,c∈(0,1)
这么写是错误的,因为极限变量n在被积函数中,以积分∫10xndx∫10xndx为例,
似乎看起来是∫10xndx=cn,c∈(0,1)∫10xndx=cn,c∈(0,1),但实际上
当n=0n=0,c可以为(0,1)(0,1)之间的任意一个数
当n=1n=1,c=0.5c=0.5
当n=2n=2,c=1√3c=1√3
...
综上,c随着n的变化而变化,上式=cnn,cn∈(0,1)cnn,cn∈(0,1)
故由积分中值定理第一性,原式=limn→∞cnn√1+c2n,cn∈(0,1)limn→∞cnn√1+c2n,cn∈(0,1),此时正确
-
当c∈(0,1)c∈(0,1),是否limn→∞cn=0limn→∞cn=0
例:limn→∞(nn+1)n=1elimn→∞(nn+1)n=1e
-
-
-
几何意义:通常结合积分上下限变化
-
f(x)f(x)图像:
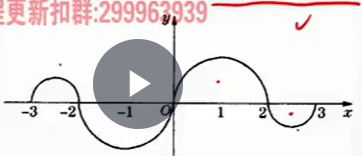
对于F(x)=∫x0f(x)dxF(x)=∫x0f(x)dx:F(2)=F(−2),F(3)=F(−3)F(2)=F(−2),F(3)=F(−3)
原因:∫abf(x)dx=−∫baf(x)dx(a<b)∫abf(x)dx=−∫baf(x)dx(a<b)
-
利用区间可加性
例:设连续函数f(x)满足f(x+2)−f(x)=x,∫20f(x)dxf(x+2)−f(x)=x,∫20f(x)dx,求∫31f(x)dx∫31f(x)dx
- 由f(x+2)−f(x)=xf(x+2)−f(x)=x,显然可将区间[a,b]=>[a+2,b+2]/[a−2,b−2][a,b]=>[a+2,b+2]/[a−2,b−2]
- 考虑到[0,2],[1,3][0,2],[1,3]的
- 相同区间为[1,2]
- 不相同区间为[0,1],[2,3]
- 为使用f(x+2)−f(x)=x,∫20f(x)dxf(x+2)−f(x)=x,∫20f(x)dx,显然应该将[2,3]变作[0,1]区间
注:感受命题人的思路
-
-
-
定积分计算
-
积分区间为nπnπ:优先考虑周期性
例:I=∫nπ0√1−sin2xdx=n∫π0√1−sin2xdxI=∫nπ0√1−sin2xdx=n∫π0√1−sin2xdx
-
去绝对值
I=∫π0\abscosx−sinxdxI=∫π0\abscosx−sinxdx
-
分区间
I=∫π40cosx−sinxdx+∫3π4π4sinx−cosxdxI=∫π40cosx−sinxdx+∫3π4π4sinx−cosxdx
-
转换积分区间
I=∫5π4π4sinx−cosxdxI=∫5π4π4sinx−cosxdx
-
-
利用分部积分求导
例:设f(x)=∫x0sintπ−tdtf(x)=∫x0sintπ−tdt,计算I=∫π0f(x)dxI=∫π0f(x)dx
I=xf(x)|π0−∫π0xf′(x)dx=π∫π0sintπ−tdt−∫π0tsintπ−tdt=2I=xf(x)|π0−∫π0xf′(x)dx=π∫π0sintπ−tdt−∫π0tsintπ−tdt=2
注:这里uv|bauv|ba结算后出现了ππ与积分
-
向参数方程转化
∫bay(x)dx=∫dcy(t)x′(t)dt∫bay(x)dx=∫dcy(t)x′(t)dt
注:dx=x′dtdx=x′dt
证明:
令x=x(t)x=x(t),则有
I=∫dcy(x(t))x′(t)dtI=∫dcy(x(t))x′(t)dt
注:证明是在y(x)y(x)中代入x(t)x(t),实际上一般题目中直接给了y(x)y(x)
-
-
变上限定积分函数及其应用
常用性质:
-
连续性
f(x)f(x)在[a,b][a,b]上可积,则F(x)=∫xaf(t)dtF(x)=∫xaf(t)dt在[a,b][a,b]上连续
注:函数可积,意味着原函数处处可导(导数存在,函数处处连续)
-
可导性
-
f(x)连续,F(x)=∫xaf(t)dtF(x)=∫xaf(t)dt可导(导函数连续,原函数处处可导)
-
f(x)f(x)由第一类间断点
-
可去间断点:F′−(x0)=F′+(x0)=F′(x0)=limx→x0f(x)≠f(x0)F′−(x0)=F′+(x0)=F′(x0)=limx→x0f(x)≠f(x0)
即有F(x)F(x)可导
-
跳跃间断点:F′−(x0)≠F′+(x0)F′−(x0)≠F′+(x0)
即有F(x)F(x)不可导,但连续(因为至少左右导数是存在的,如:F(x)={x2sin1x,x≠00,x=0F(x)={x2sin1x,x≠00,x=0)
-
-
-
奇偶性:从F(x)F(x)是f(x)f(x)的一个原函数角度去理解
-
周期性:变上限积分F(x)F(x)(更准确的说是对于所有原函数)是周期函数当且仅当∫T0f(x)dt=0∫T0f(x)dt=0
例:sinxsinx的原函数显然都是周期函数,但sinx+1sinx+1的原函数则不是
利用积分中值定理定理求极限不可导部分f(x)f(x)(TODO:可以添加到极限计算中)
-
-
例:设函数f(x)f(x)连续,且f(0)≠0f(0)≠0,求极限limx→0∫x0(x−t)f(t)dtx∫x0f(x−t)dtlimx→0∫x0(x−t)f(t)dtx∫x0f(x−t)dt
I=limx→0∫x0f(t)dt∫x0f(t)dt+xf(x),f(0)≠0=limx→0xf(c)xf(c)+xf(x)I=limx→0∫x0f(t)dt∫x0f(t)dt+xf(x),f(0)≠0=limx→0xf(c)xf(c)+xf(x)
注:
-
法二:等价代换,f(x)≈f(0)(x→0)f(x)≈f(0)(x→0)(未曾设想的道路)
- 法三:直接用积分中值定理
变上限积分去绝对值:定义域分区间讨论
例:f(x)=∫x−1(1−\abs1)dtf(x)=∫x−1(1−\abs1)dt
f(x)={∫x−1(1+t)dt,x<=1∫0−1(1+t)dt+∫x0(1+t)dt,x>1f(x)={∫x−1(1+t)dt,x<=1∫0−1(1+t)dt+∫x0(1+t)dt,x>1
-
积分不等式
常用方法:
-
定积分不等式性质:函数不等式,介值不等式,绝对值不等式
-
变量代换:可结合区间再现
-
积分中值定理
-
转为变上限积分:求导
如:证明∫a0f(x)dx>=a∫10f(x)dx∫a0f(x)dx>=a∫10f(x)dx
可令F(a)=∫a0f(x)dx−a∫10f(x)dxF(a)=∫a0f(x)dx−a∫10f(x)dx
-
柯西积分不等式:积分的平方或平方的积分
(∫baf(x)g(x)dx)2<=∫baf2(x)dx∫bag2(x)dx(∫baf(x)g(x)dx)2<=∫baf2(x)dx∫bag2(x)dx
注:
- 对于单个函数f(x)f(x)有(∫baf(x)dx)2<=∫baf2(x)dx∫ba12dx=(b2−a2)∫baf2(x)dx(∫baf(x)dx)2<=∫baf2(x)dx∫ba12dx=(b2−a2)∫baf2(x)dx
- 有正有负乘法叠加的平方 <= 正数叠加 平方的乘法
题型:
-
选择题:定积分排大小顺序
- 定积分的性质:结合常用不等式
- 基于假设:由于所给定积分的积分区间相同,故只需比较函数大小即可,而函数关系通常是恒大于或恒小于的
- 特值法
- 当积分在0点附近:等价无穷小
-
填空题
常见题型,已知f(x)=g(x)+If(x)=g(x)+I,若g(x)g(x)已知,I为对f(x)f(x)的积分
- 若I的定积分:积分
- 若I的变上限积分:求导构造微分方程
-
证明题
-
两边都是积分
-
积分区间不同
-
通过变量代换转换到同一个区间
-
两个区间有包含关系:拆分成两个无关的区间
-
∫∫向∑∑的转化
例:证明\abs∫10f(x)dx−1n∑nk=1f(kn)<=M2n\abs∫10f(x)dx−1n∑nk=1f(kn)<=M2n
由于右侧有n,故无法通过求极限使用定积分的定义消去∑∑,只能将∫∫向∑∑形式转化
- 左侧:∫10f(x)dx=∑nk=1∫knk−1nf(x)dx∫10f(x)dx=∑nk=1∫knk−1nf(x)dx
- 右侧:注意到kn−k−1n=1nkn−k−1n=1n,故有1n∑nk=1f(kn)=∑nk=1∫knk−1nf(kn)1n∑nk=1f(kn)=∑nk=1∫knk−1nf(kn)
故原式左侧=∑nk=1∫knk−1n[f(x)−f(kn)]dx∑nk=1∫knk−1n[f(x)−f(kn)]dx
-
-
积分区间相同:比较f(x),g(x)f(x),g(x)
-
结合f(x)f(x)的单调性:变上限定积分
复杂式:∫a+∫bag(t)dtaf(x)dx<=∫baf(x)g(x)dx∫a+∫bag(t)dtaf(x)dx<=∫baf(x)g(x)dx
令F(u)=∫a+∫uag(t)dtaf(x)dx<=∫uaf(x)g(x)dxF(u)=∫a+∫uag(t)dtaf(x)dx<=∫uaf(x)g(x)dx
-
联系f(x),f′(x)f(x),f′(x)时
-
积分中值定理:f(x)−f(a)=f′(ξ)(x−a)f(x)−f(a)=f′(ξ)(x−a)
-
右侧含有f′(x)f′(x)的积分时:使用变上限积分f(x)=∫x0f′(t)dtf(x)=∫x0f′(t)dt
f(x)−f(0)=∫x0f′(x)dxf(x)−f(0)=∫x0f′(x)dx作为积分放缩的两个方向:
- 被积函数放缩
- 被积区间放缩:可联系单调性
注:
- f2(x)=[∫x0f(x)dx]2f2(x)=[∫x0f(x)dx]2放缩
- 被积函数放缩:结合柯西不等式,有(∫x0f′(x)dx)2<=x∫x0f′2(x)dx(∫x0f′(x)dx)2<=x∫x0f′2(x)dx
- 被积区间放缩:结合f′2(x)f′2(x)单调性,x∫x0f′2(x)dx<=x∫10f′2(x)dxx∫x0f′2(x)dx<=x∫10f′2(x)dx
-
分部积分法
-
-
-
-
-
反常积分
-
无穷区间上的反常积分
与定积分的区别:不是和式极限,而是定积分取极限
定积分可计算称为可积,反常积分可计算称为收敛
定义:
- ∫+∞af(x)dx=limt→+∞∫taf(x)dx∫+∞af(x)dx=limt→+∞∫taf(x)dx
- ∫+∞−∞f(x)dx=∫0−∞f(x)dx+∫+∞0f(x)dx∫+∞−∞f(x)dx=∫0−∞f(x)dx+∫+∞0f(x)dx
判别法:
- 比较判别法
- 比较判别法的极限形式
比较对象:∫+∞a1xPdx{−P+1<0,收敛−P+1>0,发散,(a>0)∫+∞a1xPdx{−P+1<0,收敛−P+1>0,发散,(a>0)
注:
- 当P=1P=1,由lnx|+∞a=∞lnx|+∞a=∞,故发散
- 对于x→∞x→∞,显然当−P+1<0−P+1<0积分才收敛
-
无界函数的反常积分
瑕点:没有定义的点
∫baf(x)dx=limt→a+∫btf(x)dx∫baf(x)dx=limt→a+∫btf(x)dx
注:+是因为由b向a
判别法:
- 比较判别法
- 比较判别法的极限形式
比较对象:∫ba1(b−x)Pdx,∫ba1(x−a)Pdx{−P+1>0,收敛−P+1<=0,发散,(a>0)∫ba1(b−x)Pdx,∫ba1(x−a)Pdx{−P+1>0,收敛−P+1<=0,发散,(a>0)
注:
- 当P=1P=1,由limt→b−lnx|ta=−∞−lnalimt→b−lnx|ta=−∞−lna,故发散
- 对于b−x→0+b−x→0+,显然当−P+1>0−P+1>0积分才收敛
-
题型
-
反常积分的敛散性
过程
- 向等价无穷小转换化简
- 根据自变量x是趋向0还是趋向无穷选择p积分比较
例:判断∫∞1lnx(1+x)x1−pdx∫∞1lnx(1+x)x1−pdx收敛时的p取值范围
- lnx(1+x)x1−plnx(1+x)x1−p~1x2−p1x2−p
- 由x→∞x→∞,当1−p>11−p>1收敛
-
反常积分的计算:
-
大部分正常计算
-
无穷区间的周期函数(sinx,cosxsinx,cosx):区间分割转化为级数
例:∫∞0e−xsinxdx=∑∞k=0∫(k+1)πkπe−xsinxdx∫∞0e−xsinxdx=∑∞k=0∫(k+1)πkπe−xsinxdx
注: 奇偶性:反常积分的奇偶性只有在收敛的前提下才能用
如:∫1−11sinxdx∫1−11sinxdx
-
-
定积分应用
-
几何应用
-
平面域面积:s=∬D1dσs=∬D1dσ
-
直角坐标系下:S=∫ba[f(g)−g(x)]dxS=∫ba[f(g)−g(x)]dx
注:对x积分的含义,x轴上无数段ΔyΔy的累加
-
极坐标系下:S=∫βα[r(θ)−0]rdrS=∫βα[r(θ)−0]rdr
-
-
空间体体积
-
旋转体体积:平面域D绕直线L:ax+by+c=0L:ax+by+c=0旋转所得
dσdσ表示是区域的微分,r(x,y)r(x,y)为平面域一点到直线距离,dVdV为平面上一块小区域绕直线旋转一周的圆环体积,故dV=2πr(x,y)dσdV=2πr(x,y)dσ
则有:V=2π∬Dr(x,y)dσV=2π∬Dr(x,y)dσ
计算:
-
确定被积函数:r(x,y)=\absax+by+c√a2+b2r(x,y)=\absax+by+c√a2+b2
注:仅在确定被积函数时用到旋转轴,下面就是正常的积分计算
-
化为极坐标:仅适用于积分区域为扇形
-
化为累次积分
- 定外层积分限:穿针法
- 定内层积分限:确定边界
-
常用公式
- Vx=π∫bary2dxVx=π∫bary2dx
- Vy=π∫barx2dyVy=π∫barx2dy
注:
- 本质上都是对圆环的积分
- 默认先积y,如果先积x公式正好相反
-
-
已知横截面面积的体积
V=∫baS(x)dxV=∫baS(x)dx
-
-
曲线弧长
- 直角坐标系:s=∫ba√1+y′2dxs=∫ba√1+y′2dx
- 参数方程坐标系:s=∫βα√x′2+y′2dts=∫βα√x′2+y′2dt
- 极坐标系:s=∫βα√r2+r′2dθs=∫βα√r2+r′2dθ
- 直角坐标系:s=∫ba√1+y′2dxs=∫ba√1+y′2dx
-
旋转体侧面积(结合弧长公式)
Sx=2π∫baf(x)√1+f′2(x)dxSx=2π∫baf(x)√1+f′2(x)dx
注:即2πr2πr乘以弧长的微分√1+f′2(x)dx√1+f′2(x)dx
-
-
物理应用
- 压力
- 变力做功
- 引力
-
题型
-
几何应用
-
极轴:θ=0θ=0的轴
-
求旋转体体积
-
若横截面规则:直接使用横截面面积公式
例:x2+y2<=1(y<=12)x2+y2<=1(y<=12)
S=∫12−1πx2dyS=∫12−1πx2dy
由于边界满足x2+y2=1x2+y2=1,故S=∫12−1π(1−y2)dyS=∫12−1π(1−y2)dy
-
若横截面不规则:使用公式2π∬rdσ2π∬rdσ
-
-
-
物理应用
-
压力问题
压力=压强*面积
p=rgh
注:主要体现出同一深度的压强相同,压强随深度的变化而变化
-
变力做功
w=rgh
注:主要体现出同一深度的做工相同,做工随深度的变化而变化
-
-
四、常微分方程
常微分方程的基本概念
- 微分方程
- 阶:导数的最高阶数
- 解
- 通解:任意常数的个数等于阶数
- 微分方程的特解:通解通过初始条件定出常数
- 初始条件
- 积分曲线:解的图像
一阶微分方程
-
可分离变量的方程
y′=f(x)g(y)y′=f(x)g(y)
则有g(y)dy=f(x)dxg(y)dy=f(x)dx
注:保持dy,dxdy,dx在分母位
-
齐次方程
y′=f(yx)y′=f(yx)
-
线性方程:y′,yy′,y都是一次的
y′+P(x)y=Q(x)y′+P(x)y=Q(x)
通解公式:y=e−∫P(x)dx[∫eP(x)dxQ(x)+c]y=e−∫P(x)dx[∫eP(x)dxQ(x)+c]
证明
y′+P(x)y=Q(x)y′+P(x)y=Q(x)
e∫Pdxy′+e∫PdxPy=Qe∫Pdxe∫Pdxy′+e∫PdxPy=Qe∫Pdx
[e∫Pdxy]′=Qe∫Pdx[e∫Pdxy]′=Qe∫Pdx
e∫Pdxy=∫Qe∫Pdxdx+ce∫Pdxy=∫Qe∫Pdxdx+c
y=∫Qe∫Pdxdx+ce∫Pdxy=∫Qe∫Pdxdx+ce∫Pdx
注:
-
记推导过程比记公式更容易
-
函数∗C≠C∗C≠C
如:对于s(x)e−x=e−x1−x+cs(x)e−x=e−x1−x+c,两边同乘exex则有s(x)=11−x+Cexs(x)=11−x+Cex
-
-
伯努利方程:向线性方程转化
y′+P(x)y=Q(x)yα(α≠1)y′+P(x)y=Q(x)yα(α≠1)
解法:令y1−α=uy1−α=u,化为一阶线性
证明
原式=y′y−α+P(x)y1−α=Q(x)y′y−α+P(x)y1−α=Q(x)
令y1−α=u,y=u11−α,y′=11−αuα1−αu′y1−α=u,y=u11−α,y′=11−αuα1−αu′
上式=11−αuα1−αu′u−α1−α+P(x)u=Q(x)11−αuα1−αu′u−α1−α+P(x)u=Q(x)
u′1−α+P(x)u=Q(x)u′1−α+P(x)u=Q(x)
u′+P(x)1−αu=(1−α)Q(x)u′+P(x)1−αu=(1−α)Q(x)
-
全微分方程
前提:du=Pdx+Qdydu=Pdx+Qdy
P(x,y)dx+Q(x,y)dy=0P(x,y)dx+Q(x,y)dy=0
判断:∂P∂y=∂Q∂x∂P∂y=∂Q∂x
解法:
-
凑微分
验算:du=u′xdx+y′ydydu=u′xdx+y′ydy
-
偏积分
-
线积分
-
可降价的高阶方程
-
y″=f(x)y′′=f(x)
-
y″=f(x,y′)y′′=f(x,y′):先求y′y′
-
y″=f(y,y′)y′′=f(y,y′):转化为对y积分,即令y′=p,y″=pdpdyy′=p,y′′=pdpdy
例:解微分方程yy″=y′2yy′′=y′2
令y′=p,y″=pdpdyy′=p,y′′=pdpdy
则有ypdpdy=p2ypdpdy=p2,可分离
高阶线性微分方程
-
线性微分方程的解的结构(仅理论)
(1)齐次方程:y″+p(x)y′+q(x)y=0y′′+p(x)y′+q(x)y=0
(2)非齐次方程:y″+p(x)y′+q(x)y=f(x)y′′+p(x)y′+q(x)y=f(x)
则有:
-
若y1(x),y2(x)y1(x),y2(x)是齐次方程的两个线性无关的特解
则(1)通解:y=C1y1(x)+c1y2(x)y=C1y1(x)+c1y2(x)
-
若y∗y∗是非齐次方程(2)的一个特解,y1(x)y1(x)和y2(x)y2(x)是齐次方程(1)的两个线性无关的特解
则(2)通解:y=C1y1(x)+C1y2(x)+y∗(x)y=C1y1(x)+C1y2(x)+y∗(x)
-
若y∗1(x),y∗2(x)y∗1(x),y∗2(x)是非齐次方程(2)的两个特解
则(1)通解:y=y∗1(x)−y∗2(x)y=y∗1(x)−y∗2(x)
-
若y∗1(x),y∗2(x)y∗1(x),y∗2(x)是非齐次方程(21),(22)(21),(22)的两个特解
则(21)+(22)(21)+(22)通解:y=y∗1(x)+y∗2(x)y=y∗1(x)+y∗2(x)
总结非齐次方程的解,齐次部分解,非齐次部分解:
y″+p(x)y′+q(x)y=f(x)y′′+p(x)y′+q(x)y=f(x),非齐次方程解y1,y2y1,y2
- 由于非齐次方程解的差是齐次部分解:y齐=y1−y2y齐=y1−y2
- 由于非齐次方程解与齐次部分解的差是非齐次部分解:y非=y1−y齐y非=y1−y齐
- 非齐次方程解与非齐次部分解的关系:两者都满足非齐次方程,但非齐次方程解还包含了齐次方程解
-
-
常系数齐次线性微分方程
常系数,指p,qp,q均为常数
形式:y″+py′+qy=0y′′+py′+qy=0
特征方程:r2+pr+q=0r2+pr+q=0
设r1,r2r1,r2是特征方程的两个根
- 若r1≠r2r1≠r2:y=C1er1x+C2er2xy=C1er1x+C2er2x
- 若r1=r2r1=r2:y=erx(C1+C2x)y=erx(C1+C2x)
- 若r1,2=α±iβr1,2=α±iβ:y=eαx(C1cosβx+C2sinβx)y=eαx(C1cosβx+C2sinβx)
-
常系数非齐次线性微分方程
y″+py′+qy=f(x)y′′+py′+qy=f(x)
-
若f(x)=Pm(x)eλxf(x)=Pm(x)eλx
令y∗=xkQm(x)eλxy∗=xkQm(x)eλx
注:对于x2+1x2+1可看做(x2+1)e0x(x2+1)e0x
-
若f(x)=eαx[Pl(x)cosβx+Pn(x)sinβx]f(x)=eαx[Pl(x)cosβx+Pn(x)sinβx]
令y∗=xkeαx[R(1)m(x)cosβx+R(2)m(x)sinβx].m=max(l,n)y∗=xkeαx[R(1)m(x)cosβx+R(2)m(x)sinβx].m=max(l,n)
注:
- k为非齐次解是齐次方程的特征方程的几重根
- 由于共轭复根总是成对出现的,故在二阶常系数微分方程下,共轭复根的特解中的kk只能取到0或1
-
-
欧拉方程:一类特殊的线性变系数方程
∑xiy(i)=f(x)∑xiy(i)=f(x)
令x=etx=et,有xky(k)=D(D−1)...(D−k+1)y(D=dydt)xky(k)=D(D−1)...(D−k+1)y(D=dydt)
证明
令x=etx=et,有y′x=dydx=dydtdtdx=y′txy′x=dydx=dydtdtdx=y′tx
则xy′x=y′txy′x=y′t
...
xky(k)=D(D−1)...(D−k+1)y(D=dydt)xky(k)=D(D−1)...(D−k+1)y(D=dydt)
题型
-
微分方程求解
如:解微分方程xy′−y=−xxy′−y=−x,计算后得y=−xlnx+cxy=−xlnx+cx,代入原微分方程后通过
化简计算:
-
找原函数法
对于xf″(x)+f′(x)=0xf′′(x)+f′(x)=0
显然有[xf′(x)]′=0[xf′(x)]′=0,xf′(x)=Cxf′(x)=C
无法直接判断微分方程类型
-
换元:根据y′,yy′,y项考虑换元。
使用:分离变量转化为一阶线性形式ψ(y′)+φ(y)=f(x)ψ(y′)+φ(y)=f(x),若ψ′(y)=φ(y)ψ′(y)=φ(y),则令u=φ(y)u=φ(y)
例:y2−2x=yy′y2−2x=yy′
- 转化为一阶线性形式:yy′−y2=−2xyy′−y2=−2x
- 考虑到(y2)′=2yy′(y2)′=2yy′,故可令t=y2t=y2,则有t′−2t=−4xt′−2t=−4x
-
x,y关系对调
-
一阶:出现1y′1y′更好计算时
例:y′=1xy+y3y′=1xy+y3
对调后:dxdy=xy+y3dxdy=xy+y3
-
二阶:当出现−y″y′3−y′′y′3
例:y″+(x+e2y)y′3=0y′′+(x+e2y)y′3=0
由于x″=−y″y′3x′′=−y′′y′3,故上式=−x″+x+e2y=0−x′′+x+e2y=0
-
-
非直接的f(x),f′(x),f″(x)f(x),f′(x),f′′(x)关系:消元,如:再次求导
例:f′(x)=−f(−x),(1)f′(x)=−f(−x),(1)
再求导得f″(x)=f′(−x),(2)f′′(x)=f′(−x),(2)
联立(1),(2)消去f′(x)f′(x)可得f″(x)+f(x)=0f′′(x)+f(x)=0
P(x,y)dy+Q(x,y)dy=0P(x,y)dy+Q(x,y)dy=0形式
- 若∂P∂x≡∂Q∂y∂P∂x≡∂Q∂y:求原函数
- 凑微分
- 偏积分
- 若不是全微分:化为含y′y′的y′+f(x,y)=0y′+f(x,y)=0形式
已知方程特解,求二阶线性(非常系数)微分方程y″+P(x)y′+Q(x)y=f(x)y′′+P(x)y′+Q(x)y=f(x)
- 找到方程的通解
- 由两个方程特解相减找到两个线性无关的齐次特解y1,y2y1,y2,故由齐次部分的通解为y齐=c1y1+c2y2y齐=c1y1+c2y2
- 由方程特解减去齐次部分特解找到非齐次部分特解:y∗y∗
- 故方程通解为:y=y齐+y∗=c1y1+c2y2+y∗y=y齐+y∗=c1y1+c2y2+y∗
- 求微分方程:
- 求齐次方程部分
- 由yy求得y′,y″y′,y′′,将y,y′,y″y,y′,y′′代入y″+P(x)y′+Q(x)y=0y′′+P(x)y′+Q(x)y=0
- 消去不定系数c1,c2c1,c2即可得p(x),Q(x)p(x),Q(x)
- 求非齐次方程部分:代入y″+P(x)y′+Q(x)y=f(x)y′′+P(x)y′+Q(x)y=f(x)一个较为简单的非齐次部分特解f(x)f(x)
- 求齐次方程部分
注:同求二阶线性常系数微分方程比较
- 求通解部分相同,都是找到两个线性无关的齐次方程解
- 求微分方程部分,求齐次方程部分不同;求非齐次方程部分相同,都是代入一个较为简单的非齐次方程部分特解
- 对于非常系数微分方程:需要将y″,y′,yy′′,y′,y代入求得P(x),Q(x)P(x),Q(x)(是一个更通用的解法)
- 对于常系数微分方程:可以直接通过特征公式求常系数P,QP,Q
例:已知二阶非齐次线性微分方程的特解y1=3,y2=3+x2,y3=3+exy1=3,y2=3+x2,y3=3+ex,求方程的通解以及微分方程
由y2−y1=x2,y3−y1=exy2−y1=x2,y3−y1=ex,有齐次部分通解y齐=c1x2+c2exy齐=c1x2+c2ex
由y2−x2=3y2−x2=3,有非齐次部分通解y∗=3y∗=3
故y=c1x2+c2ex+3y=c1x2+c2ex+3
求得y′=2c1x+c2ex,y″=2c1+c2exy′=2c1x+c2ex,y′′=2c1+c2ex
由二阶非齐次线性微分方程,有二阶线性非齐次方程形式y″+P(x)y′+Q(x)y=f(x)y′′+P(x)y′+Q(x)y=f(x)
将y″,y′,yy′′,y′,y代入二阶线性齐次方程部分2c1+c2ex+P(x)(2c1x+c2ex)+Q(x)(c1x2+c2ex+3)y=02c1+c2ex+P(x)(2c1x+c2ex)+Q(x)(c1x2+c2ex+3)y=0
消去c1,c2c1,c2
有{2+2xP(x)+Q(x)x2=0ex+exP(x)+exQ(x)=0=>{P(x)=x2−22x−x2Q(x)=2−2x2x−x2{2+2xP(x)+Q(x)x2=0ex+exP(x)+exQ(x)=0=>{P(x)=x2−22x−x2Q(x)=2−2x2x−x2
将非齐次部分解y=3y=3代入y″+P(x)y′+Q(x)y=f(x)y′′+P(x)y′+Q(x)y=f(x),有f(x)=32−2x2x−x2f(x)=32−2x2x−x2
故方程的通解为y″+x2−22x−x2y′+2−2x2x−x2y=32−2x2x−x2y′′+x2−22x−x2y′+2−2x2x−x2y=32−2x2x−x2
除分母丢解问题:
如:对于2yududy=1−u2,u=g(y)2yududy=1−u2,u=g(y)
分离变量有2u1−u2du=1ydy2u1−u2du=1ydy
由于u=g(y)u=g(y)是一个关于y的函数,故除分母后丢失的解有y=0,u=g(y)=±1y=0,u=g(y)=±1
-
-
综合题
-
函数方程:结合ΔxΔx形式导数定义limΔx→0f(x+Δx)−f(x)ΔxlimΔx→0f(x+Δx)−f(x)Δx化为微分方程
注:由一般性的导数定义向某个特殊点的导数定义转化
如:函数方程f(x+y)=exf(y)+eyf(x),f′(0)=2f(x+y)=exf(y)+eyf(x),f′(0)=2
由导数定义及函数方程有
f′(x)=limΔx→0exf(Δx)+eΔxf(x)−f(x)Δxf′(x)=limΔx→0exf(Δx)+eΔxf(x)−f(x)Δx
=limΔx→0exf(Δx)Δx+f(x)eΔx−1Δx=limΔx→0exf(Δx)Δx+f(x)eΔx−1Δx
=exf′(2)+f(x)=exf′(2)+f(x)
-
证反常积分∫∞0ydx∫∞0ydx收敛并求值
例:y″+2y′+ky=0,0<k<1y′′+2y′+ky=0,0<k<1
-
证反常积分∫∞0ydx∫∞0ydx收敛:只需证y=C1er1x+C2er2xy=C1er1x+C2er2x中,r1<0,r2<0r1<0,r2<0
-
求∫ydx∫ydx,可用微分方程y″+2y′+ky=0y′′+2y′+ky=0代入简化计算
-
-
-
应用题
-
求面积:优先尝试结合规则的几何图形公式求解
例:

-
法一:通过集合面积关系求面积
观察可得,梯形oxPB的面积为S=(1+y)x2S=(1+y)x2
故直接可得S=∫x0f(x)dx−xy+x2=x3S=∫x0f(x)dx−xy+x2=x3
-
法二:先求直线方程,再求面积S
求直线方程Y−1=y−1x(X−0)(0<X<x)Y−1=y−1x(X−0)(0<X<x),Y=y−1xX+1Y=y−1xX+1
对XX进行积分,则有S=∫x0f(X)−(y−1xX+1)dx=x3S=∫x0f(X)−(y−1xX+1)dx=x3
整理可得S=∫x0f(x)dx−xy+x2=x3S=∫x0f(x)dx−xy+x2=x3
注:这里是在区间(0,x)(0,x)对XX积分
注:
- 注意x,Xx,X的区别与关系(如这里的(0<X<x)(0<X<x)),以及对谁积分
- 计算面积时需保证长宽等参数为正数
-
-
求曲线方程
设(x,y)(x,y)为f(x)f(x)上任一点,(X,Y)(X,Y)为切线或法线上一点
-
构造所需要的切线或法线公式
-
切线:Y−y=f′(x)(X−x)Y−y=f′(x)(X−x)
y轴截距:Y=−xf′(x)+yY=−xf′(x)+y
x轴截距:X=−yf′(x)+xX=−yf′(x)+x
-
法线:Y−y=−1f′(x)(X−x)Y−y=−1f′(x)(X−x)
-
-
求得所需点,向量
-
根据题意列出向量的关系式:注意倒数等
-
解微分方程
-
根据题意列出初始条件:可结合连续性,极值
-
-
求温度等
-
根据关系列微分方程
例:该物体温度对时间的变化率与该时刻物体和介质的温度差成正比
dTdtT−t0=kdTdtT−t0=k
-
定常数
-
根据方程求想要的结果
-
-
出来一个常数,定一个常数
-
五、多元微分学
重极限,连续,偏导数,全微分
间断点不学:太复杂了
-
重极限
-
概念:lim(x,y)→(x0,y0)f(x,y)=Alim(x,y)→(x0,y0)f(x,y)=A
注:洛必达,Taylor公式,等价无穷小无法使用
-
计算常用方法
-
初步判断分子与分母次数
- 若分子高:0
- 若相同:不存在(不同方向所求的极限不相等)
- 若分母高:趋向无穷
-
根据初步判断选择证明方法
-
证明极限为0:
-
取绝对值:lim(x,y)→(x0,y0)f(x,y)=0lim(x,y)→(x0,y0)f(x,y)=0=>lim(x,y)→(x0,y0)\absf(x,y)=0lim(x,y)→(x0,y0)\absf(x,y)=0
-
夹逼:放缩
-
和1比较:\absx2yx2+y2<=\absy\absx2yx2+y2<=\absy
注:若分子为多个项相加,可以拆项
例:证明lim(x,y)→(0,0)√x2+y2=0lim(x,y)→(0,0)√x2+y2=0
lim(x,y)→(0,0)√x2+y2lim(x,y)→(0,0)√x2+y2
=lim(x,y)→(0,0)x2+y2√x2+y2lim(x,y)→(0,0)x2+y2√x2+y2
=lim(x,y)→(0,0)x2√x2+y2+lim(x,y)→(0,0)y2√x2+y2lim(x,y)→(0,0)x2√x2+y2+lim(x,y)→(0,0)y2√x2+y2
<=lim(x,y)→(0,0)x√x2+y2∗x+lim(x,y)→(0,0)y√x2+y2∗ylim(x,y)→(0,0)x√x2+y2∗x+lim(x,y)→(0,0)y√x2+y2∗y
<=lim(x,y)→(0,0)x+lim(x,y)→(0,0)ylim(x,y)→(0,0)x+lim(x,y)→(0,0)y
=0
-
对分母使用不等式a2+b2>=2aba2+b2>=2ab
-
-
-
证明极限不存在:不同方向的极限不同
-
使用y=kxy=kx
注:无法表示x=m线
-
-
-
-
-
连续
-
偏导数
-
定义法
代入一侧,对另一侧求导数:fx(x0,y0)=limΔx→0f(x0+Δx,y0)−f(x0,y0)Δxfx(x0,y0)=limΔx→0f(x0+Δx,y0)−f(x0,y0)Δx
-
求某个具体点的偏导数:先代后求(转化为求一元函数的导数)
-
几何意义:fx(x0,y0)fx(x0,y0)表示曲线f(x,y0)f(x,y0)在x=x0x=x0的切线
-
高阶偏导数
若f″xy(x,y),f″yx(x,y)f′′xy(x,y),f′′yx(x,y)在D内连续
则f″xy(x,y)=f″yx(x,y)f′′xy(x,y)=f′′yx(x,y)
注:本质上任然是一元函数的导数
-
-
全微分
前提(必要条件):A=fx(x0,y0)A=fx(x0,y0)与B=fy(x0,y0)B=fy(x0,y0)都存在
常见定义
-
Δz=f(x0+Δx,y0+Δy)−f(x0,y0)=AΔx+BΔy+o(ρ)Δz=f(x0+Δx,y0+Δy)−f(x0,y0)=AΔx+BΔy+o(ρ)
改写为极限形式:limΔx→0,Δy→0[f(x0+Δx,y0+Δy)−f(x0,y0)]−[AΔx+BΔy]√(Δx)2+(Δy)2=0limΔx→0,Δy→0[f(x0+Δx,y0+Δy)−f(x0,y0)]−[AΔx+BΔy]√(Δx)2+(Δy)2=0
-
Δz=f(x,y)−f(x0,y0)=A(x−x0)+B(y−y0)+o(ρ)Δz=f(x,y)−f(x0,y0)=A(x−x0)+B(y−y0)+o(ρ)
改写为极限形式:limx→x0,y→y0[f(x,y)−f(x0,y0)]−[A(x−x0)+B(y−y0)]√(x−x0)2+(y−y0)2=0limx→x0,y→y0[f(x,y)−f(x0,y0)]−[A(x−x0)+B(y−y0)]√(x−x0)2+(y−y0)2=0
已知函数的全微分定义式,求函数的f(x0,y0),f′x(x,y),f′y(x,y)f(x0,y0),f′x(x,y),f′y(x,y)
例:f(x,y)=1−x−y+o(√(x−1)2+y2)f(x,y)=1−x−y+o(√(x−1)2+y2)
- 由lim(x,y)→(1,0)f(x,y)=f(1,0)=0lim(x,y)→(1,0)f(x,y)=f(1,0)=0
- 故由全微分定义f′x=−1,f′y=−1f′x=−1,f′y=−1
判定
- 充分条件:fx(x,y)fx(x,y)和fy(x,y)fy(x,y)在(x0,y0)(x0,y0)连续
- 定义
- fx(x0,y0)fx(x0,y0)与fy(x0,y0)fy(x0,y0)是否都存在
- limΔx→0,Δy→0[f(x0+Δx,y0+Δy)−f(x0,y0)]−[AΔx+BΔy]√(Δx)2+(Δy)2=0limΔx→0,Δy→0[f(x0+Δx,y0+Δy)−f(x0,y0)]−[AΔx+BΔy]√(Δx)2+(Δy)2=0
-
-
连续,可导,可微的关系
可导:在多元函数中具体指两个偏导数f′x(x0,y0),f′y(x0,y0)f′x(x0,y0),f′y(x0,y0)存在
与一元的区别:
-
可导不一定连续:二元可导只能说明两个方向的连续
-
可导不一定可微:导数存在,但其关系可能不满足极限的定义
-
可微一定连续
-
对于一元
可微定义:dy=f′(x0)dx+o(x)dy=f′(x0)dx+o(x)
连续定义:limx→x0f(x)−f(x0)=0limx→x0f(x)−f(x0)=0
由于可微,故f′(x0)f′(x0)存在,即limx→x0f(x)−f(x0)x−x0limx→x0f(x)−f(x0)x−x0存在,故limx→x0f(x)−f(x0)=0limx→x0f(x)−f(x0)=0
即有可微一定可导,可导一定连续,故可微一定连续
-
对于多元
可微定义:dz=f(x,y)−f(x0,y0)=f′x(x0,y0)(x−x0)+f′y(x0,y0)(y−y0)+ρdz=f(x,y)−f(x0,y0)=f′x(x0,y0)(x−x0)+f′y(x0,y0)(y−y0)+ρ
连续定义:lim(x,y)→(x0,y0)f(x,y)−f(x0,y0)=0lim(x,y)→(x0,y0)f(x,y)−f(x0,y0)=0
由可微定义,要证lim(x,y)→(x0,y0)f(x,y)−f(x0,y0)=0lim(x,y)→(x0,y0)f(x,y)−f(x0,y0)=0
只需证lim(x,y)→(x0,y0)f′x(x,y)(x−x0)−f′y(x,y)(y−y0)+ρ=0lim(x,y)→(x0,y0)f′x(x,y)(x−x0)−f′y(x,y)(y−y0)+ρ=0
显然,由于ρ=o(√(x−x0)2+(y−y0)2)ρ=o(√(x−x0)2+(y−y0)2),该极限成立,故可微一定连续
-
-
偏导数连续一定可微:充分条件,通过二重极限lim(x,y)→(x0,y0)fx(x,y)=fx(x0,y0)lim(x,y)→(x0,y0)fx(x,y)=fx(x0,y0)定义
-
-
题型
讨论连续性,可导性,可微性
-
基本证明
- 证明偏导数连续:设f(x,y)f(x,y)在(x0,y0)(x0,y0)间断
- 使用定义求f′x(x0,y0)f′x(x0,y0)
- 使用公式求f′x(x,y)f′x(x,y)
- 若limx→x0f′x(x,y0)=f′x(x0)limx→x0f′x(x,y0)=f′x(x0),则偏导数连续
- 证明可微:limx→x0,y→y0[f(x,y)−f(x0,y0)]−[A(x−x0)+B(y−y0)]√(x−x0)2+(y−y0)2=0limx→x0,y→y0[f(x,y)−f(x0,y0)]−[A(x−x0)+B(y−y0)]√(x−x0)2+(y−y0)2=0
-
有界性证明(TODO:可以整理到计算中去)
- 用绝对值不等式拆分分子
- 对分数拆项
\absΔx−Δy√(Δx)2+(Δy)2\absΔx−Δy√(Δx)2+(Δy)2<=\absΔx+\absΔy√(Δx)2+(Δy)2<=2\absΔx+\absΔy√(Δx)2+(Δy)2<=2
-
抽象函数与全微分公式的关系
limx→x0,y→y0[f(x,y)−f(x0,y0)]−[A(x−x0)+B(y−y0)]√(x−x0)2+(y−y0)2=0limx→x0,y→y0[f(x,y)−f(x0,y0)]−[A(x−x0)+B(y−y0)]√(x−x0)2+(y−y0)2=0
-
由极限与无穷小的关系
可得函数f(x,y)=f(x0,y0)+[A(x−x0)+B(y−y)]+ρf(x,y)=f(x0,y0)+[A(x−x0)+B(y−y)]+ρ
注:可以在选择题中作为特质法使用
-
(设分子除f(x,y)f(x,y)均为已知项)直接求得f(x0,y0),f′x(x0,y0)=A,f′y(x,y0)=Bf(x0,y0),f′x(x0,y0)=A,f′y(x,y0)=B
可得多元函数全微分的定义形式f(x,y)−f(x0,y0)=f′x(x−x0)+f′y(y−y0)+ρf(x,y)−f(x0,y0)=f′x(x−x0)+f′y(y−y0)+ρ
则有A=f′x,B=f′yA=f′x,B=f′y
-
-
求微分:具体函数法
例:lim(x,y)→(0,1)f(x,y)−2x+y−2√x2+(y−1)2=0lim(x,y)→(0,1)f(x,y)−2x+y−2√x2+(y−1)2=0,则dz|(0,1)dz|(0,1)=
令f(x,y)=2x−y+2f(x,y)=2x−y+2
-
可微性判定
fx(x0,y0)fx(x0,y0)存在,fy(x,y)fy(x,y)在点(x0,y0)(x0,y0)处连续,证明f(x,y)f(x,y)在店(x0,y0)(x0,y0)处可微
注:该定律看上去较弱,但可以之前的两个可微性判定更准确
-
偏导数和全微分的计算
-
复合函数求导法
设u=u(x,y),v=v(x,y)u=u(x,y),v=v(x,y)可导,z=f(u,v)z=f(u,v)在相应点有连续的一阶偏导数,则
-
∂z∂x=∂z∂u∂u∂x+∂z∂v∂v∂x=f′1u′1+f′2v′1∂z∂x=∂z∂u∂u∂x+∂z∂v∂v∂x=f′1u′1+f′2v′1
注:
- 第一部分∂z∂x∂z∂x表明最终是对xx求偏导 => u,v为中间变量
- 第二,三部分由变量关系转变为函数关系
-
∂z∂y=∂f∂u∂u∂y+∂f∂v∂v∂y∂z∂y=∂f∂u∂u∂y+∂f∂v∂v∂y
多元函数微分形式的不变性(全微分形式不变性)
设z=f(u,v),u=u(x,y),v=v(x,y)z=f(u,v),u=u(x,y),v=v(x,y)都有连续一阶偏导数
- 对于直接变量(自变量):dz=∂z∂xdx+∂z∂ydydz=∂z∂xdx+∂z∂ydy
- 对于间接变量变量(中间变量):dz=∂z∂udu+∂z∂vdvdz=∂z∂udu+∂z∂vdv
-
-
隐函数求导法
-
由一个方程所确定的隐函数
F(x,y,z)=0,Fz≠0F(x,y,z)=0,Fz≠0:z=z(x,y)
方法:
- 公式法:∂z∂x=−FxFz,∂z∂y=−FyFz
- 等式两边求导
- 微分形式的不变性:Fxdx+Fydy+Fzdz=0
-
由方程组确定的隐函数
-
-
题型
-
求一点处的偏导数与全微分
求∂z∂x|(0,1):先代后求法
-
求z|y=1
-
求∂z∂x|x=0=z′x|x=0=z′x(0)
注:第二步求偏导,第三步代入
一阶偏导:
- 连续:直接先代后求
- 分段点:也可以先代(化为一元函数)后求(一阶偏导)
二阶偏导:一阶求,二阶代
多元函数的微分:对于f(x,y,z,...),有df(z,y,z,...)=f′xdx+f′ydy+f′zdz+...
-
-
求已给出具体表达式函数的偏导数与全微分
-
求偏导数
常用方法
-
函数为显函数形式且简单易求(无根号):直接求偏导,偏导数中不包含z
-
函数形式复(有根号):化为隐函数使用公式法,偏导数中包含z(通常可用于消元化简)
公式:∂z∂x=−Fx′Fz′
使用
- 平方:去根号
- 两边同乘:去分母
- 将所有变量化到同一端
- 分别求F′x,F′z
- 由公式得∂z∂x=−Fx′Fz′
例:zy=√1−x2−34y2,求∂z∂x
- 将等式按照前三步进行化简,得到z2+x2y2−y2+34y4=0
- 分别求得F′x=2xy2,F′z=2z
- 故∂z∂x=−xy2z
利用复合函数求导法求复杂多元函数(幂指函数)的偏导数
例:z=(1+x2+y2)xy
令u=1+x2+y2,v=xy
则z=uv,∂z∂x=∂z∂u∂u∂x+∂z∂v∂v∂x=vuv−1∗2x+uvlnu∗y
-
-
求原函数
- 偏积分
-
凑微分:当函数比较简单,没有分母
-
求z=f(xy,x2+y2)的二阶偏导数:注意到u,v中均有x,y,故在对f′1,f′2求二阶偏导数对u,v均需展开
-
g(t)=f[t,f(t,t2)],求g′(0):在求偏导数需要带参数,否则在代入时无法判断是内层的参数还是外层的参数
-
已知关于直接变量(自变量)和间接变量(中间变量)的条件,求参数
例:已知u=f(x,y),{ξ=x+ayη=x+by,求a,b,使等式4∂2u∂x2+12∂2u∂x∂y+5∂2u∂y2=0可以简化为∂2u∂ξ∂η=0
-
若向x,y转化:需要求∂2u∂x2,∂2u∂x∂y,∂2u∂y2
而∂2u∂x2,∂2u∂x∂y,∂2u∂y2计算的结果包含了∂2u∂ξ∂η,∂2u∂ξ2,∂2u∂η2
为了向结果∂2u∂ξ∂η=0转化,显然需令∂2u∂ξ∂η≠0,∂2u∂ξ2=0,∂2u∂η2=0
-
若向ξ,η转化:只需要求∂2u∂ξ∂η=0满足等式4∂2u∂x2+12∂2u∂x∂y+5∂2u∂y2=0
为什么不用求∂2u∂ξ2,∂2u∂η2:因为4∂2u∂x2+12∂2u∂x∂y+5∂2u∂y2=0代表了一个等式条件,只要你满足这样一个配比就能使所得为0
-
-
由极坐标向直角坐标的转换
例:u=f(r,θ),∂u∂θ=0
由题u的变化与θ无关,又r=√x2+y2,则有u=f(√x2+y2)
-
n次齐次函数:f(tx,ty)=tnf(x,y)
例:f(x,y)=xy,则f(tx,ty)=txy=t2f(xy)
充要条件:x∂f∂x+y∂f∂y=nf(x,y)
-
-
隐函数的偏导数与全微分
计算
- 变量关系简单:直接求
- 变量关系复杂:微分形式不变形
隐函数条件
- f(x,y)=0,f′y≠0=>y=f(x)
- 又f(x,y)=C为一条直线,显然只能为y=x+c形式
复合函数的隐函数求偏导
例:u(x,2x)=x,求u关于x的偏导数
分析复合函数u中的参数关系{xy→x,则
两边对x求一阶偏导,有u′1+u′22=1
两边对x求二阶偏导,有u″11+u″122+(u″21+u″222)2=0
-
极值和最值
-
无条件极值
-
定义
-
极值的必要条件
- 极值点但非驻点:f(x,y)=\absx+\absy
- 驻点但非极值点:f(x,y)=xy(在(0,0)附近即有大于0,也有小于0的值)
-
极值的充分条件
A=f″xx(x,y),B=f″xy(x,y),C=f″yy(x,y)
- AC−B2>0,有极值{A>0极小值A<0极大值
- AC−B2<0,无极值
- AC−B2=0,无法确定,需要用定义判断
注:当AC<0,必然没有极值
-
-
条件极值和拉格朗日乘数法
拉格朗日乘数法:必要条件,只能找到可能的极值,无法判断是极大值还是极小值,故通常考最值
-
最大最小值
求f(x,y)在有界闭区域D上的最大最小值
- 先求D内部可能得极值点
- 再求D边界上的最大最小值
- 比较
-
题型
-
求无条件极值
-
驻点验证:当f′x,f′y较为复杂且需要联立求公共点时,应该待会验证
例:{f′x=5x3−2y−−3xy=0f′y=2y−x2−x3
求得复杂驻点(23,1027)后应至少代入一个公式验证
-
结合几何图形
如对于(x−1)2+(y+1)2+(z−2)2=16,求z的最值
几何图形:以(1,−2,2)为中心,4为半径的球体
则z的最大值为2+4=6,最小值为2-4=-2
-
结合极限
-
极限的保号性
例:lim(x,y)→(0,0)f(x,y)sinx2+y2=−1
-
易得f(0,0)=0
-
由极限的保号性
当(x,y)在(0,0)的去心邻域,恒有f(x,y)sin(x2+y2)<0,即有f(x,y)<0
-
(0,0)点为极大值
-
-
极限和无穷小的关系
例:lim(x,y)→(0,0)f(x,y)−xy(x2+y2)2=1
易得,无法用极限的保号性
由极限和无穷小的关系,有f(x,y)=xy+(1+α)(x2+y2)2
而f(x,x)=x2+o(x2),f(x,−x)=−x2+o(x2)
故f(x,y)在(0,0)点处无极值
-
-
已知极值判定原函数的参数范围
如:f(x,y)在(x0,y0)取得极小值
则有{A>0AC−B2>0
-
-
求最大最小值(目标函数和条件函数)
-
目标函数简化
-
目标函数包含有条件函数:代入化简
例:目标函数为z=x2+y2−12x+16y,条件函数为x2+y2=25
则目标函数可以化简为z=25−12x+16y
-
含根号项:求其平方,如:点到直线的距离
-
含多项相乘:用ln拆开,如:海伦公式
-
-
问题转化
-
考察条件函数
若曲线为圆:化为关于θ的一元函数求极值问题
-
考察目标函数
几何意义:圆心到规则几何图形的距离
例:求z=(x−6)2+(y+8)2−100在x2+y2=25上的最值
即求(6,−8)到圆x2+y2=25最近和最远的距离
若规则图形:直接代入,化条件为无条
注:对于圆可以代入参数方程
-
-
解拉格朗日方程组
利用线性代数解λ后进行讨论
例:F(x,y,z,λ)=xy+2xz+λ(x2+y2+z2−10),{F′x=y+2z+2λx=0F′y=x+2yλ=0F′z=2x+2λz=0F′λ=x2+y2+z2−10=0
- 由x,y,z不同时为0,即方程组有非0解
- 故|2λ1212λ0202λ|=0可解得λ
-
-
用条件极值求不等式:设一端为k
例:证abc3<=2755(a+b+c)5
令a+b+c=k,只需证abc3<=2755k5
由Lagrange乘数法,令F(x,y,z,λ)=xyz3+λ(x+y+z−k)
注:本题实际上也可以用基本不等,由于abc3=33∗a∗b∗c3∗c3∗c3,
由基本不等式a+b2>=√ab=>a+b+c+d+e5>=5√abc
则当a=b=c3,有abc3=33∗a∗b∗c3∗c3∗c3<=33(a+b+c3+c3+c35)5
-
六、二重积分
-
二重积分的概念
-
定义:∬Df(x,y)dσ=limd→0∑nk=1f(ξk,ηk)Δσk
-
几何含义:曲顶柱体的体积
注:
-
同样是和式极限,但是点乘以面积
-
不能是面质量,因为二维平面不存在质量的概念,一型曲面积分代表了平面质量的概念
-
重积分与累次积分的区别
- 以二重积分为例,其定义的微元是ds
- 显然这是无法计算,但是当被积函数可以通过两个变量x,y(θ,r)定义,我们也可以将ds拆成两个微元的计算,如ds=dxdy=rdθdr,此时可以化为多个定积分的计算,即累次积分
-
-
二重积分的几何意义:曲顶柱体的体积
-
二重积分的性质
- 不等式性质
- 被积函数
- 连续函数
- 绝对值
- 积分中值定理
- 不等式性质
-
二重积分计算:化为累次积分
-
利用直角坐标计算
-
先y后x
先y:y2(x)−y1(x)
-
先x后y
先x:x1(y)−x2(y)
注:如何由图像确定要积分对象
二重积分化为累次积分,先积分对象是点,后积分对象为线
例:∬Dydxdy,D:x=−2,y=0y=2,x=−2√2y−y2
图像
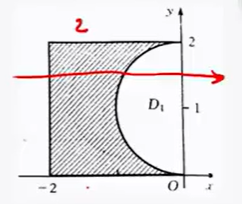
- 显然二重积分的外层积分对象如箭头所示,由于外层积分的是x轴上的点,故显然是对x的积分dx,积分显然是要向另一个变量y转化,故积分的上下限都为x关于y的函数
- 内层:由上可知,是对y的积分dy,积分上下限为y的最小与最大值(如果没有重叠部分)
- 故累次积分为:∫20dy∫−2√2y−y2−2ydx
-
-
利用极坐标计算
-
公式:∬Df(x,y)dσ=∫θ2θ1dθ∫r2r1f(rcosθ,rsinθ)rdr
注:当D为原x2+y2=a时,r=√a,这是一个易错的点
-
适合用极坐标的被积函数:
- f(√x2+y2):可以化为关于r的一元函数
- f(yx),f(xy):可以化为关于θ的一元函数
-
适合用极坐标的积分域:
设积分域为圆心为(x0,y0)的圆,则可令{x−x0=rcosθy−y0=rsinθ
注:
-
确定$\theta 积分区域:对于多个\cos \theta,\sin \theta通过三角函数和差公式转化为同一个\cos \theta或\sin \theta$
例:积分区域x2+y2<=x+y
代入x=rcosθ,y=rsinθ
对于边界有r=cosθ+sinθ=√2sin(θ+π4)
显然当0<=θ+π4<=π,即有−π4<=θ<=3π4时,r>0
-
-
轮换对成性:
当D关于y=x对称,有∬Df(x,y)dσ=∬Df(y,x)dσ
-
使用雅各布行列式计算二维参数方程的积分
例:求f2(x)+g2(y)=a2
- 确定参数方程:开方,即有{f(x)=rcosθg(y)=rsinθ
- 由于参数方程对应的不一定是传统意义的极坐标,故使用雅各布行列式计算微元dxdydz=\abs∂(x,y)∂(r,θ)drdθ
- 列出表达式
例:x23+y23=1
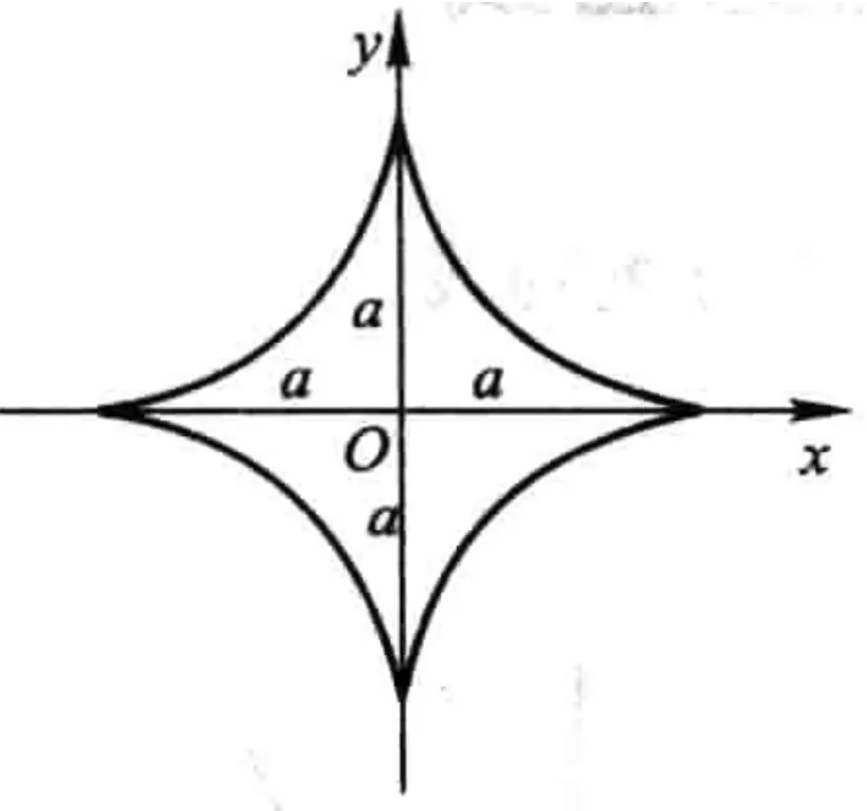
-
{x=rcos3θy=rsin3θ
-
dxdydz=\abs∂(x,y)∂(r,θ)drdθ
=|3r2cos3θ−3r3cos2θsinθ3r2sin3θ−3r3sin2θcosθ|drdθ
=9r5sin2θcos5θdrdθ
-
I=∫10dr∫2π09r5sin2θcos5θdrdθ=38π
-
-
题型
-
计算二重积分
基本思路:
-
考察积分区域
-
是否沿x轴/y轴对称
特殊奇偶性:
-
可分割的奇偶对称性:
例:y=x3,y=1,x=−1围成的区域D
补充曲线y=−x3,将区域D分割为左侧的D1,上侧D2,则D1关于x轴对称,D2关于y轴对称
适用的被积函数:f(x,y)=xy
-
可平移的奇偶对称性
例:计算∬D(x+y)dσ,D:x2+y2<=x+y
注意到D关于x=12,y=12对称
故原式=∬D(x+12)+(y+12)−1dσ=∬D1dσ
-
-
是否沿y=x轴对称(轮换对称性)
-
是否为两个规则图形加减:将原积分拆开
利用形心公式计算:¯x=∬Dxdσs=>∬Dxdσ=¯xs
-
-
考察被积函数
-
若积分区域关于x轴/y轴对称:考察函数奇偶性
例:∬Dydσ
由被积函数当积分变量为+y,−y时才能抵消,故应该关于x轴对称
-
若积分区域关于y=x轴对称:考察轮换对称性,通常用极坐标计算
为什么∬y>=xxe−(x2+y2)dσ=∬x>=yye−(x2+y2)dσ?
由轮换对成性的定义,将左式积分区间和被积函数的x,y对换,即为右式
-
二重积分换元:实际上就是对内层线积分进行换元
例:I=∫badθ∫−2asinθ0r2√4a2−r2dr
令r=2asint,则I=∫badθ∫−θ02a2(1−cos2t)dt
-
特殊方法:
-
边界曲线为参数方程形式:先写成直角坐标系的累次积分,然后代入参数方程
-
复杂函数确定积分区间:
例:f(x)={x,−1<=x<=20,其它
求f(x2−y)的积分区间
令−1<=x2−y<=2
只需确定边界−1=x2−y,x2−y=2
-
被积函数有绝对值:令被积函数=0,分区间去绝对值
例:∬D\absx2+y2−2ydσ
令x2+y2−2y=0,显然在圆内的被积函数为负,在圆外的被积函数为正
-
根据被积函数,对轮换对称性逆用
例:∫10f(x)dx=A,求∫10dx∫1xf(x)f(y)dy
积分区域D1:x<=y<=1,0<x<1
由轮换对成性定义,对换积分区域,被积函数的x,y值
显然被积函数不变,积分区域变为D2:y<=x<=1,0<y<1
令D=D1+D2:0<=x<=1,0<=y<=1
则有I=12[∬D1f(x)f(y)σ+∬D2f(x)f(y)σ]=12∬Df(x)f(y)dσ=12A2
-
换元:雅各宾行列式求微元
在直角坐标系下,对于二重积分有I=∬Df(x,y)dσ=∬Df(x,y)dxdy
若{x=P(u,v)y=Q(u,v)
则有dxdy=\absJdudv
其中\absJ=∂(x,y)∂(u,v)=|∂x∂u∂x∂v∂y∂u∂y∂v|
例:对于D:(x−1)2+(y−1)2=1,求I=∬Ddσ
显然,根据集合意义可知I=π
倘若使用坐标系平移
{x−1=rcosθy−1=rsinθ
则有\absJ=|cosθ−rsinθsinθrcosθ|=r
故dxdy=rdrdθ
-
-
累次积分交换次序及计算:通常题目给出的是累次积分,而非二重积分形式,先考率交换积分次序,再考虑交换坐标系
-
积分上下限有交替变换
例:I=∫20dx∫xx2f(x,y)dy
由对y的积分可知
- 当0<=x<=1,y=x2在下,y=x在上,由下往上积分
- 当1<=x<=2,y=x在下,y=x2在上,由上往下积分
原式=∫10dx∫xx2f(x,y)dy−∫21dx∫x2xf(x,y)dy
注:
- 积分限由下到上且由左到右:正数使用黑笔填充
- 积分限由上到下或由右到左:负数使用红笔填充
-
极坐标转为先θ后r
对照:
- 先r后θ:是引以θ为常数的一条射线
- 先θ后r:是引以r为常数的一个圆弧
-
对于累次积分看做内外层嵌套的定积分:对于内层定积分,可以单独进行换元
-
-
与二重积分有关的综合题:基本思想,还是往一元看
-
化为定积分,求导解微分方程
-
累次积分对x求导
[∫x0dt∫u20f(t,u)du]′=[∫x0(∫u20f(t,u)dt)du]′=∫x20f(t,x)d
注:将内层函数的所有u用x替换
-
偏导数定积分求原函数
∫cosθfx(rcosθ,rsinθ)+sinθfy(rcosθ,rsinθ)dr=f(rcosθ,rsinθ)+c
-
将原函数与高阶导数联系起来
- Lagrange中值定理或Taylor公式
- 分部积分法
-
连乘的定积分转化为累次积分:两个相乘的定积分是可分离的二重积分,积分区域为矩形
∫baf(x)dx∫ba1f(x)dx=∫baf(x)dx∫ba1f(y)dy=∬Df(x)f(y)dσ
-
-
与二重积分有关的不等式问题:排顺序
-
考虑被积函数复合的单调性
例:I1=∬Dcos√x2+y2dσ,I2=∬Dcosx2+y2dσ,I3=∬Dcos(x2+y2)2dσ,D:x2+y2<=1
对于内层函数有√x2+y2<=x2+y2<=(x2+y2)2
对于外层函数有cos(√x2+y2)<=cos(x2+y2)<=cos(x2+y2)2
-
定积分化为二重积分:两个相乘的定积分是可分离的二重积分,积分区域为矩形
例:f(x),g(x)在[0,1]上连续且单调增,证明∫10f(x)g(x)dx>=(∫10f(x)dx)(∫10g(x)dx)
-
-
七、无穷级数
定义级数的部分和为Sn=∑nk=1ak,则无穷级数S=limn→∞Sn=limn→∞∑nk=1ak
常数项级数
-
级数的概念与性质
概念:无穷个数的和
性质:
-
∑∞n=1un收敛 => limn→∞un=0
-
级数收敛:通项不一定是单减,可以是震荡
如:∑∞n=1[2+(−1)n]12n
- 证明收敛:将an拆开为两项可知收敛
- 证明不单调:an+1an=2+(−1)n+12[2+(−1)n]
- 当n=2k:an+1an=16<1
- 当n=2k+1:an+1an=32>1
-
加括号提高收敛性,加绝对值提高发散性
注:这里加括号提高收敛性是指在一个级数中,对于不同的两个级数∑(an+bn),∑an+∑bn收敛性仍然相同
-
加减或改变有限项不影响级数的敛散性
注:可以不去关注前有限项
-
∑un收敛到s,则∑kun也收敛,且收敛到ks
注:∑an收敛,∑bn收敛,则∑anbn收敛
-
由于无穷级数是通过部分和的极限定义的,故an也可使用极限的某些特性,如皮亚诺余项的Tyalor公式
例:y′=x+y,y(0)=1讨论∑∞n=1[y(1n)−1−1n]的敛散性
将y=1+x+x2+o(x2),故由y(1n)−1−1n≈1n2,级数收敛
注:可以理解为an的无限项可能趋向0的速度是1n2
-
-
级数的审敛准则
-
正项级数
-
比较判别法
若an,bn绝对收敛,则由\absan±bn<=\absan+\absbn,有\absan±bn收敛
-
比较法极限形式
-
比较对象:
-
p级数(调和级数)
∑∞n=11np:显然当p>1,级数项趋向于0的速度才足够快
注:∑∞n=11nlnn发散
-
等比级数(几何级数)
∑∞n=1aqn:显然当q<1,级数项趋向于0的速度才足够快
-
-
等价无穷小判断收敛性:基于比较法的极限形式故仅适用于正项级数,无法用于交错级数
例:∑(−1)n[1√n+(−1)nn]
显然1√n+(−1)nn≈1√n且∑(−1)n1√n收敛
但是∑(−1)n[1√n+(−1)nn]=∑(−1)n1√n+1n=收敛+发散=发散
注:由于收敛级数的通项趋向于0,若不收敛到0必然是发散,若收敛到0只需比较其发散的快慢程度
-
-
和自己比:结合极限
- 比值法:limn→∞un+1un=ρ{收敛,ρ<1发散,ρ<1不一定,ρ=1
- 根值法:limn→∞n√un=ρ{收敛,ρ<1发散,ρ<1不一定,ρ=1
-
积分判别法
条件:an=f(x),f(x)单调减,非负,连续
结论:∑∞n=1an与∫+∞1f(x)dx同敛散
注:易证∑∞n=11n发散
-
-
交错级数:∑∞n=1(−1)n−1un,un>0
莱布尼兹准则
条件:
- un单调减
- limn→∞un=0
则级数收敛
注:
- 交错级数收敛不一定满足莱布尼兹准则,如增加有限的非递减项,不改变级数的收敛性
- Un不包含(−1)n−1
-
任意项级数:绝对值收敛 => 原级数收敛
绝对收敛与条件收敛
- 绝对值收敛,原级数都收敛:绝对收敛
- 绝对值发散,原级数收敛:条件收敛
-
-
题型
-
求级数的一般思路
- 正项级数
- 比值判别法和根值判别法
- 比较法的极限形式:等价无穷小,求导
- 其它如积分判别法,放缩等
- 交错级数:莱布尼兹准则
-
正项级数敛散性的判定
使用
-
根据级数类型考虑比值判别法和根植判别法
1lnpn>1nα>1an>1n!>1nn
-
比值判别法或根植判别法:an,n!,nn
-
比较判别法或比较判别法的极限形式:lnpn,np
注:通常可以结合放缩,转向已知极限或定义
-
-
比较法的极限形式:通过等价无穷小向求极限转换
-
比较判别法
放缩:一般放缩分母以证明收敛性
如:∑√n∫n04√1+x4dx<=∑√n∫n0xdx
注:注意到分子的积分是不可积
-
积分判别法:如:un=1xlnpx
-
通过Taylor展开判断敛散性
例:∑∞n=1ln(1+(−1)n√n)
-
通过比较判别法放缩证明发散
ln(1+(−1)n√n)>ln(1+(−1)√n)
由于小的发散,故大的发散
-
通过Taylor公式证明发散性
ln(1+(−1)n√n)=(−1)n√n−121n+o(1n)
由于Taylor展开后的第一项为收敛,第二项为发散,故整体为发散
注:对于正项级数内部的变项无法使用等价无穷小,且使用Taylor展开需要到非交错项
-
常用结论:
-
un收敛,则u2n收敛
证明:u2n<un
-
正项数列an单调减少 => liman存在
注:有单调有下界,故收敛,且收敛到大于或等于0的位置
-
-
交错级数敛散性的判定
复杂形式
-
正弦函数:利用诱导公式提取(−1)n
例:sin(π√n2+a2)单调性判断和求极限
I=sin[nπ+(π√n2+a2−nπ)]
=(−1)nsin(π√n2+a2−nπ)
=(−1)nsina2π√n2+a2+n
-
余弦函数:cos(nπ)=(−1)n
注:求级数结果中的所有cos(nπ)项均不保留
-
拆项
如:∑∞n=1(−1)nxnn[(−3)n+2n]=(−1)nn−(−23)nn[1+(−23)n]
-
-
任意项级数敛散性的判定
-
通解:
-
通项是否趋于0
注:对于\absan,若由正项级数的比值法和根植法判断ρ>1说明发散,则原级数也发散(正项级数递增,说明极限不趋向于0)
-
绝对值>原级数>括号(收敛性由低到高,发散性由高向低排列)
注:
- 高收敛性向低收敛性放缩,以证明高收敛性级数的收敛
- 高发散性向低发散性放缩,以证明高发散性级数的收敛
-
回归定义:通常前后项能相消
-
-
利用级数定义讨论收敛性
- 若limn→∞an≠0:必然发散
- s=∑amn−amn+1必收敛:s=(am1−am2)+(am2−am3)+...+(amn−amn+1)=am1−amn+1
-
绝对收敛与条件收敛加减关系(类似收敛与发散的关系)
-
绝对收敛±绝对收敛=绝对收敛
-
绝对收敛±条件收敛=条件收敛
-
条件收敛±条件收敛=绝对未定
例:an=(−1)nn,bn=(−1)n+1n
使用
-
∑∞n=1un条件收敛 => ∑∞n=1un±\absun2发散(发散+收敛=发散)
-
结合不等式
例:∑∞n=1a2n收敛,求∑∞n=1\absan√n2+λ
由不等式2ab<=a2+b2
\absan√n2+λ<=12(a2n+1n2+λ)
-
-
讨论收敛性:绝对收敛=>条件收敛 => 发散
例:讨论∑∞n=11annp的收敛性
-
常见反例
-
加法和减法:都用交错级数举反例
-
∑(u2n−1−u2n)收敛反例
原级数:1−12+13−14...
加括号:(1+12)+(13+14...)
即:b1=(a1+a2)=(1+12)
-
-
-
证明题与综合题
-
结合Taylor公式:向高阶放缩证收敛性
例:f(x)在x=0邻域内有二阶连续导数,且limf(x)x=0,证明∑f(1n)绝对收敛
由题,有f(1n)<=M21n2,由∑1n2收敛,故∑f(1n)收敛
-
向已知的p级数(调和级数)或等比级数转化(调和级数)转化
\absun+1−un<=...<=hn\absu1−u0,h<1
显然,级数∑\absun+1−un可以转化为通项是公比小于1的等比级数,故原级数收敛
-
-
幂级数
-
收敛半径,收敛区间,收敛域
-
阿贝尔定理
- 当∑anxn当x=x0(x0≠0)时收敛,则大概\absx<\absx0时,∑anxn绝对收敛
- 当∑anxn当x=x0(x0≠0)时发散,则大概\absx>\absx0时,∑anxn发散
- 当∑anxn当x=x0(x0≠0)时条件收敛,则x=x0为收敛区间与发散区间分界点
-
求收敛半径
-
比值法:若limn→∞\absan+1an=ρ,则R=1ρ
证明
- limn→∞\absan+1an=ρ,有limn→∞\absan+1xn+1anxn=ρx
- 由正项级数的比值审敛法,有当rx<1收敛,即x<1ρ
- 故收敛为R=1ρ
注:后项比前项是为了凑x
-
根值法:若limn→∞√\absan=ρ,则R=1ρ
-
-
-
幂级数的性质
-
运算性质:两个级数相加减,则收敛半径取交集R=min(R1,R2)
注:对于R外的有理运算性质需要具体问题具体分析
-
分析性质
-
连续性:收敛域上连续
-
可导性:收敛区间上逐项可导
每求导一次实际上少一项:(∑∞n=0anxn)′=∑∞n=0nanxn−1=∑∞n=1nanxn−1
-
可积性:收敛域上逐项可积
-
-
-
函数的幂级数展开
f(x)在x=x0处的Taylor级数:∑f(n)(x0)n!(x−x0)n
-
幂级数展开的唯一性
-
常用展开式
-
11−x=∑∞n=0xn(−1<x<1)
注:
- 由和函数的定义域可知:x≠1
- 由无穷级数的定义∑∞n=01=∞可知:x≠−1
-
ex=∑∞n=0xnn!(−∞<x<∞)
-
sin(x)=∑∞n=0(−1)nx2n+1(2n+1)!(−∞<x<∞)
arctanx=∑∞n=0(−1)nx2n+1(2n+1)(−1<=x<=1)
注:
- −1<=x<=1由11+x的展开式推得
- arctanx与sinx展开唯一的区别在于没有阶乘符号!
-
cos(x)=∑∞n=0(−1)nx2n(2n)!(−∞<x<∞)
-
ln(1+x)=∑∞n=0(−1)n−1xnn(−1<x<=1)
-
(1+x)α=1+αx+α(α−1)2!x2..
注:级数下标统一从0开始
-
-
函数展开幂级数的两种方法
- 直接展开法
- ∑∞n=0xnn=−ln(1−x)(−1<=x<1)
- 间接展开法
- 先求导后积分:只能用变上限积分f(x)−f(a)=∫xaf′(x)dx,不能用不定积分
- 先积分后求导
- 直接展开法
-
幂级数参数调整
-
调整an或xn的上标
例:对于∑∞1(−1)nxn−1,通过调整级数下标改变xn−1为xn
- 令n1=n+1,则原式=(−1)n1+1xn1
- 为保证首项不变,使n1+1=n=1,故起始位n1=0
上式=∑∞0(−1)n+1xn
-
调整an和xn的上标
如:∑∞n=2anxn,向∑∞n=1anxn−1转化
-
调整系数a的下标:通过调整n的起始值
I=x∑∞n=2anxn−1
-
调整x的指数:乘以或除以x
上式=x∑∞n=2anxn−1
-
调整n的起始值:添项或减项(对标准形式使用)
上式=x(∑∞n=1anxn−1−a1)
原因:
- an为抽象系数,最难调整
- x可以通过乘除调整
- 级数下标可以通过加减调整,最容易
-
-
-
-
题型
-
求收敛区间及收敛域
-
当幂级数为y=f(x),yn形式
例:∑(−1)nan(x−1)2n
令y=(x−1)2,易得ρ=limn→∞\absan+1y2(n+1)any2n=ρy2
则收敛半径R=1ρy2<1,−1√ρ<y<+1√ρ
-
无法直接用公式求ρ:拆项(奇偶项)
-
根据条件收敛确定收敛中心
例:∑(x−a)nn在x=−2处条件收敛
由阿贝尔易得ρ=1,R=1
由x=−2为条件收敛点,故中心点a=−3或a=−1
令y=x−a
- 当a=−1:y=−1,∑(−1)nn条件收敛
- 当a=−3:y=1,∑(1)nn发散
综上a=−1
注:看上去有三个变量x,−a,n,但其中n来自级数本身,x给定了限制条件x=−2时条件收敛,故实际只有一个变量a
-
-
将函数展开为幂级数
-
axax+b在x=c点的展开
- 消去分子的x项:ax+b−bax+b
- 构造x−c点:1a(x−c+c)+b=1a(x−c)+ac+b
- 化为所使用的幂级数的和函数的标准形式:1a(x−c)ac+b+1
- 使用1x+1的展开式展开
-
先求导后积分:反三角函数
如:f(x)=arctanx=∫11+x2dx
-
先积分后求导
如:f(x)=1(x+2)2=−(1x+2)′
-
在x=x0点展开:将f(x)转换为f(x−x0)
-
求具体点的高阶导数
Taylor级数标准形式:f(x)=∑f(n)(x0)n!(x−x0)n
-
分段函数展开:
-
先展开连续部分的级数
-
考察级数是否包含该间断带点
-
若包含:直接和并为同一个级数
注:s(0)=a0
如:s(x)=∑∞n=0(−1)n2n+1x2n,s(0)=a0=1
-
若不包含:写作分段函数
-
注:在解微分方程的时候也由类似的操作
-
-
-
级数求和函数
-
类型判断
- n系数
- 分子
- 有(−1)n:sinx,cosx
- 分母
- 简单类型:ln1+x
- 阶乘类型:ex
- 无分母:11+x
- 分子
- n系数
-
y=∑∞n=0xmn(mn)!
- y只有1m项
- 结合微分方程:y=y(m)
例:求∑∞n=0x2n(2n)!的原函数
y″=∑∞n=1x2n−2(2n−2)!=∑∞n=0xn(n)!=y
-
-
求导与积分
-
若an有n系数分子:先积分后求导
例:∑∞n=0(−1)nn+1(2n+1)!x2n+1
由n系数的分母可知,对应sinx,cosx类型
由sinx,cosx的级数可知需要化解n系数的分子:应该先积分后求导
I=[∑∞n=0(−1)n1(2n+1)!x2n+2∗12]′
-
提变量x:可以对剩余部分做求导和积分,级数代换
例:∑∞n=0(−1)nn+1(2n+3)!x2n
- 提取1x3有:1x3∑∞n=0(−1)nn+1(2n+3)!x2n+3
- 部分求导后有:1x3∫x0∑∞n=0(−1)nn+1(2n+2)!x2n+2dx
- 部分代换后有:12x3∫x0xsinxdx
-
-
常数项级数转幂级数:n次方下的常数底数,可以为分数,−1
-
向n项和类型数列极限转化
-
证通项小于1的等比级数
如:an+1=an+an−1,证∑∞n=1anxn−1收敛并求和函数
-
证收敛性:放缩
由题,易知an递增
an+1=an+an−1<=2an<=...<=2na1xn−1
由等比级数的收敛性可知,当\abs2x<1,级数收敛
-
求和函数
I=1+x+∑∞n=2an+1xn=1+x+∑∞n=2(an+an−1)xn
化为标准型后有s(x)=1+x+x[s(x)−a1]+x2s(x)
-
-
-
傅里叶级数
-
傅里叶系数和傅里叶级数
f(x)~a02+∑∞n=1(ancosnx+bnsinnx)
当周期为[−π,π]
- an=1π∫π−πf(x)cosnxdx
- bn=1π∫π−πf(x)sinnxdx
注:
- 由b0=0可知与bn搭配的奇函数sinnπxl
- 级数下标n从1开始
-
收敛定理(狄利克雷)
收敛性:连续或有有限个第一类间断点,且 只有有限个极值点,则处处收敛
收敛于:
- 连续:收敛于f(x)
- 间断或端点:收敛于左右极限的平均值
注:
- 幂级数展开要求任意阶可导
- 实际上都收敛到了两点极限的平均值
-
函数展开为傅里叶级数
周期为[0,π]:奇(偶)延拓
周期为[−l,l]:
- an=1l∫l−lf(x)cosnπxldx
- bn=1l∫l−lf(x)sinnπxldx
-
题型
重点在于傅里叶系数和狄利克雷定理
傅里叶系数只记住三个
-
f(x)=a02+∑∞n=1ancosnπxl+bncosnπxl
f(x)=a02+∑∞n=1(ancosnx+bnsinnx)
-
an=1l∫l−lf(x)cos(nπxl)dx
an=1π∫π−πf(x)cos(nx)dx
-
有关收敛定理的问题
-
将函数展开为傅里叶级数
过程
-
展开
注:合并加减中的0项,如[(−1)n−1−1]={0,n=2k−1−2,n=2k
-
收敛性判定:通过狄利克雷收敛定理判断一下间断点或端点收敛到的位置是否和f(x)相同,确定级数的收敛域是闭区间还是开区间
例:f(x)=10−x,5<=x<=15
则有s(x)=10π∑∞n=1(−1)nnsinnπx5
由狄利克雷收敛定理,s(5)=s(15)=f(5)+f(15)2=0
而f(5)=5,f(15)=−5,故收敛域为(5,15)
求给定级数:如:已知某个函数的傅里叶级数展开s(x),求∑∞n=11n2
- 在所求的傅里叶级数中代入具体点,如x=0,x=1
- 级数拆奇偶项:∑∞n=11n2=∑∞n=01(2n+1)2+∑∞n=11(2n)2
非原点对称的周期:[a,a+2l],照原来的求即可
如:an=1l∫a+2laf(x)cosnπxldx
奇偶延拓:使用奇偶性,不用求另一端的具体函数
以偶延拓为例,已知f(x)(0<=x<=π)
- bn=0
- an=1π∫π−πf(x)cosnxdx=2π∫π0f(x)cosnxdx
使用傅里叶级数求给定级数的和
常用公式:由∑∞n=11n2=∑∞k=11(2k)2+∑∞k=01(2k+1)2,有34∑∞n=11n2=∑∞n=01(2n+1)2
-
-
八、向量代数与空间解析几何及多元微分学在几何上的应用
内容
- 向量代数
- 直线与平面
- 曲线与曲面
- 多元微分学与几何:运用多元微分学求曲线的切向量和曲面的法向量
向量代数
向量→a(x1,y1),→b(x2,y2)
-
点乘(数量积)
-
计算
- 坐标:→a⋅→b=x1∗x2+y1∗y2
- 边长与夹角:→a⋅→b=\abs→a\abs→bcos<→a,→b>
-
几何意义
-
求夹角:cosθ=→a⋅→b\abs→a\abs→b
-
求向量→a在向量→b上的投影(图中黄色部分):\abs→a∗cosθ=→a⋅→b\abs→b
-
-
-
叉乘(向量积)
-
几何意义:平行四边形面积
证明:
- 由sinθ的几何意义可知,\abs→asinθ为平行四边形的高(图中黄色部分)
- 由平行四边形的面积=底乘以高,故叉乘的结果为平行四边形面积
-
计算
-
边长与夹角:→a×→b=\abs→a∗\abs→b∗sinθ
-
坐标:→a×→b=x1∗y2−y1∗x2
证明:基于三角形面积
-
已知→a×→b表示三角形面积的两倍
-
又该三角形的面积可以看做两个梯形减去一个梯形(通过向量的坐标平移将梯形退化为了三角形),即有
S△AOB=S△AOC+SACDB−SBOD
=x1y12+(y2−y1)(x2−x1)2−x2y22
=\absx2y1−x1y22
-
由叉乘的坐标公式可知,第一个点的x坐标乘以第二个点的y坐标减去第二个点的y坐标乘以第一个点的x坐标,显然当第一个点的x较大,第二个点的y坐标较大时结果为正,对应右手系
-
故→a×→b=x1∗y2−y1∗x2,得证
-
-
-
-
混合积
几何意义:六棱锥体积
空间平面与直线
-
平面方程
- 一般式
- 点法式
- 截距式
-
直线方程
- 一般式
- 对称式
- 参数式
-
平面与直线的位置关系
- 直线的方向向量
- 平面的法线向量
注:夹角一般按锐角处理
-
点到平面的距离
d=\absAx0+By0+Cz0+D√A2+B2+C2
-
点(x,y,z)到直线L:x−x1l=y−y1m=z−z1n的距离
理解:通过平行四边形的面积定义
→l={l,m,n}
d=\abs→AB×→l\abs→l
曲面与空间曲线
-
曲面方程:一般式
-
空间曲线
-
一般式,参数式
-
母线与准线
- 若母线为{x=1y=1,准线为x2+y2=1
- 则母线绕准线旋转一周可得柱面{x2+y2=1−∞<=x<=+∞
注:母线与准线可以单独出现构成不同形体
-
-
常见曲面
-
空间曲线投影:如在xoy面投影,则令z=0
-
题型
-
建立旋转面方程
-
曲线绕准线旋转:一般特指x,y,z轴
-
空间直线绕准线旋转
例:求直线L:x−10=y1=z−12绕z轴旋转所得旋转面方程
-
设点
设(x,y,z)为旋转面上任一点,它对应曲线L上的点为(x0,y0,z0)
-
考察旋转曲面上点与L上的点关系,将x0,y0,z0向x,y,z转换
-
转化z0
由绕z轴旋转,z=z0
-
转化x0,y0
由直线L方程与z的关系有L:x0−10=y01=z−12
-
x0=1
注:空间直线某一个方向的方向向量为0,相当于x0=0z−12+1斜率为0,此时x为常量
-
y0=z−12
-
-
-
构建最终表达式
由到z轴的距离,有x2+y2=x20+y20
故F(x,y,z)={z=0x2+y2=1+(z−12)2
注:也可以归纳为,绕谁转,谁不变(如x);另一个参数为y=√x2+y2
-
-
建立锥面方程
例:设锥面Σ(0<=z<=1)的顶点为A(0,0,1),准线为{(x+1)2+y2=1z=0,求Σ的方程
-
设曲面上任意一点M(X,Y,Z)
-
找关系式联立准线方程
令准线上任意一点为B(x,y,0),显然有¯AM//¯AB,即有Xx=Yy=Z−1−1
故{x=X1−Zy=Y1−Z
-
代入准线方程有Σ:[X+(1−Z)]2+Y2=(1−Z)2
注:与空间直线绕准线旋转类似,只是这里用的是平行关系,而不是直接令Z=z
-
-
-
多元微分在几何上的应用
-
曲面的切平面与法线:法向量→n=(F′x,F′y,F′z)
- 对于z=f(x,y),有→n=(f′x,f′y,−1)
- 切平面方程:
-
曲线的切线与法平面:切向量→τ=→n1×→n2
-
方向导数与梯度
-
方向导数:实际上就是通过参数方程形式扩展了偏导数的定义
-
定义:∂f∂l(x0,y0)=limt→0+f(x0+tcosα,y0+tcosβ)−f(x0,y0)t
注:实际上是用参数方程表示方向
-
几何意义:当方向导数大于0,函数值沿某一个方向递增
-
计算:若z=f(x,y)可微,则有∂f∂l=∂f∂xcosα+∂f∂ycosβ
偏导数与方向导数的区别:
-
例:z=√x2+y2的偏导数与方向导数
偏导数:由于左右两侧导数不同,不存在
方向导数:由方向导数的定义可知,∂f∂l(x0,y0)=limt→0+f(tcosα,tcosβ)−0t=1
-
总结
-
偏导数是统一的两个方向,且各方向的偏导数必须相同;(注意到t→0+)方向导数是独立的多个方向,且个方向的方向导数可以不同
-
若fx(0,0)=A,则:
- f(x,y)在(0,0)点沿x轴负方向的方向导数为−A
- f(x,y)在(0,0)点沿x轴负方向的方向导数为A
f−x(0,0)=limx→−0f(x)−f(0)x=1
而∂f∂l(−1,0)=limt→0+f(−t,0)−f(0,0)t
=limu→0−f(u,0)−f(0,0)−u
=−f−x(0,0)=−1
-
-
-
梯度
- 矢量的两个维度的含义
- 方向:与最大方向导数相同
- 大小:向量的模表示方向导数的最大值和最小值的绝对值
- 计算:gradz=∂f∂xi+∂f∂yj
- 矢量的两个维度的含义
-
-
题型
-
建立曲面的切平面和法线方程
-
基本的思想:仍然是从线切面法出发,考察向量间的关系
求函数在某点处的方向导数
例:求u=F(x,y,z)在点A(x0,y0,z0)处的方向导数
→n={F′x(x0,y0,z0),F′y(x0,y0,z0),F′z(x0,y0,z0)}
-
曲面在一点处的切平面:F′x(x−x0)+F′y(y−y0)+F′z(z−z0)=0
-
-
建立空间曲线的切线和法平面方程
求切向量或法向量
例:z=√x2+y2
- 化简表达式:z2−x2−y2=0
- 求法向量:{x,y,−z}
-
方向导数和梯度的计算
- 结合Lagrange函数:求方向导数在给定约束条件下的最大值
-
九、多元积分学及其应用
三重积分与线面积分
重积分计算式重基础,曲线曲面积分(包括二型线面)重代入,二型曲线曲面积分计算主要是使用格林公式(二维),高斯公式(三维)
是多种计算类型的综合和:如二型面积分通过高斯公式转为三重积分,三重积分通过先一后二转为求二重积分,二重积分通过极坐标转为累次积分
-
三重积分
定义
性质:
- 不等式性质:被积函数不等式,介值不等式,绝对值不等式
- 中值定理
计算
-
利用奇偶性:面对称,化简被积函数
-
利用轮换对称性:
-
规则:f(x,y,z)=f(y,z,x)=f(z,x,y)
注:向前进一位,即x=>y,y=>z,z=>x
-
使用
- 积分区域为柱:构造r=√x2+y2
- 积分区域为球:构造r=√x2+y2+z2
-
-
先二后一:截面法,计算较为简单
使用条件:
- 被积函数:仅与一个变量有关,如:z
- 积分区域:Ω的横截面为关于被积函数变量的规则几何图像S=s(z),常见的有圆,椭圆,半圆(半球体)
I=∭Ωf(z)dv=∫baf(z)S(z)dz
-
先一后二:合盖法,具有一般性
使用条件:
- 被积函数:可以包含多个变量
- 积分区域:可以表达为被z=g1(x,y),z=g2(x,y)包裹
I=∭Ωf(x,y,z)dv=∬Ddσ∫g2(x,y)g1(x,y)f(x,y,z)dz
注:这里g为关于x,y的二次函数
-
球坐标:∭Ωf(x,y,z)dσ=∫φ2φ1dφ∫θ2θ1dθ∫r2r1f(rsinφcosθ,rsinφsinθ,rcosφ)r2sinφdr
适合被积函数中自变量为r=√x2+y2+z2
推导:
-
修改被积函数:由极坐标系引申到球面坐标系
-
z=rcosφ
注:φ与z轴相关,表示从z正半轴到z负半轴,区间为[0,π]
-
x=rcosθ=>x=rcosθsinφ
-
y=rsinθ=>y=rsinθsinφ
-
-
修改积分上下限
- r:将表达式代入积分区域方程,解出关系式
- θ:各xoy截面在极坐标系下的角度(对于每个截面都应该是相同的)
- φ:由z正半轴开始定
-
修改积分微元:使用雅各布行列式(和多元函数微分形式的不变性有关?)
dxdydz=\abs∂(x,y,z)∂(r,θ,φ)drdθφ
=\abs|cosθsinφ−rsinθsinφrcosθcosφsinθsinφrcosθsinφrsinθcosφcosφ0−rsinφ|drdθdφ
=r2sinφdrdθdφ
-
-
对弧长的线积分(第一型线积分)
定义:∫Lf(x,y)ds=limλ→0∑ni=1f(ξi,ni)Δsi
性质:与积分路径无关
-
对坐标的线积分(第二型线积分):变力做功
坐标:指向量的坐标形式表示
定义:
W=→F→S
=limλ→0∑nk=1→F(ξi,ηi)→Mi−1Mi
=limλ→0∑ni=1[P(ξi,ηi)Δxi+Q(ξi,ηi)Δyi]
=∫LPdx+Qdy
性质:∫−LPdx+Qdy=−∫LPdx+Qdy(与积分路径有关)
直接法:∫LPdx+Qdy=∫βα[P(x(t),y(y))x′t+Q(x(t),y(t))y′t]dt
注:用参数方程统一
格林公式
-
基本使用
条件:
-
考察积分区间:封闭曲线L外逆内正
-
考察被积函数:P,Q在D内连续可导
注:由于初等函数在定义区间连续且可导,故在题目中通常只需考察被积函数的连续性(是否有奇点)
结论:∮LPdx+Qdy=∬D(∂Q∂x−∂P∂y)dσ
-
-
路径无关
-
判定:∂Q∂x≡∂P∂y
原因
-
当L是封闭曲线且内部无奇点,由于∂Q∂x=∂P∂y,故∮LPdx+Qdy=0
-
当L不是封闭曲线(a→b),可以通过补线L1(b→a),使被积曲线封闭
I=∮L+L1−∮L1
而∮L+L1=0
故I=−∮L1=∮−L1
-
由于−L1可以是任意(a→b)的曲线,即与路径无关
-
-
当L不是封闭曲线时:改换被积函数的积分路径
-
使用原函数法计算
-
原因:
-
由一元函数的变上限积分引申而来,由变上点积分:∫(x,y)(x1,y1)Pdx+Qdy
-
由于(x1,y1)→(x2,y2)路径无关,即(x1,y1)可以以任意方向趋向(x2,y2)
故有∫(x2,y2)(x1,y1)Pdx+Qdy
-
由牛莱公式,有I=F(x2,y2)−F(x1,y1)
-
-
结论:当∂Q∂x=∂P∂y(路径无关),由∫(x2,y2)(x1,y1)Pdx+Qdy=F(x2,y2)−F(x1,y1)
-
-
-
有奇点使用格林公式
例:∮LPdy+Qdxx2+y2,L:2x2+y2=1取逆向
显然在L内部有奇点(0,0),取L1:x2+y2=a2正向,a足够小
则有I=∮L+L1−∮L1
其中
- ∮L+L1此时无奇点,可以直接使用格林公式
- ∮L1被积函数代入积分曲线后也可以使用格林公式
两类平面线积分的联系:∮LPdx+Qdy=∮L(Pcosα+Qcosβ)ds
注:由cosα=L′x√L′2x+L′2y可知,α,β是曲线L1的切向量与坐标轴的夹角
空间曲线的计算:
斯托克斯公式
-
条件
- 考察积分区间:封闭曲线L逆时针,则∑向上(右手法则)
- 考察被积函数:被积函数P,Q,R关于x,y,z的各阶偏导数连续
-
结论
∮LPdx+Qdy+Rdz
=∬∑[cosαcosβcosγ∂∂x∂∂y∂∂zPQR]dS(一型面积分)
=∬∑(∂R∂y−∂Q∂z)dydz+(∂P∂z−∂R∂x)dzdx+(∂Q∂x−∂P∂y)dxdy(二型面积分)
注:
-
当∑为平面:化为一型面积分,因为cosα,cosβ,cosγ为常数
使用了旋度公式:向量(二型空间曲线L) => 向量{cosα,cosβ,cosγ}
-
当∑为曲面:化为二型面积分
二型面积分需确定∑方向:对L使用右手法则
-
由斯托克斯公式可知dxdy=cosγds
-
-
-
对面积的面积分(第一型面积分)
定义:∬∑f(x,y,z)dS=limλ→0∑ni=1f(ξi,ηi,ζi)ΔSi
性质:∬∑f(x,y,z)dS=∬−∑f(x,y,z)dS
-
对坐标的面积分(第二型面积分)
定义:∬∑R(x,y,z)dxdy=limλ→0∑ni=1R(ξi,ηi,ζi)(ΔSi)xy
性质:∬∑Pdydz+Qdzdx+Rdxdy=−∬−∑Pdydz+Qdzdx+Rdxdy
直接法:∬∑Rdxdy=±∬DxyRdxdy
注:需要补充的系数只可能为±1,因为dxdy限制了只对Σ在xoy面的投影(即Dxy)积分
高斯公式
-
基本使用
-
条件
- 考察积分区间:∑外表示封闭曲面外侧为正
- 考察被积函数:P,Q,R在Ω内连续且分别关于x,y,z可导,由于P,Q,R为初等函数,故一般连续即可
-
结论
∯∑外Pdydz+Qdzdx+Rdxdy
=∭Ω(∂P∂x+∂Q∂y+∂R∂z)dV
使用了散度公式:向量{P,Q,R} => 函数
-
-
有奇点使用高斯公式:补面绕过奇点
例:I=∬∑xdydz+ydzdx+zdxdy(x2+y2+z2)32,∑:x24+y29+z225=1(z>=0),上侧
补面绕过(0,0,0)点,∑1:x2+y2+z2=a2(z>0),x24+y29=1(x>1,y>1)下侧
注:这种较为复杂的补面,通过高斯转为三重积分被积函数一般较为简单可化为0
两类面积分的联系:∬∑(Pcosα+Qcosβ+Rcosγ)dS=∬∑Pdydz+Qdzdx+Rdxdy
注:
- dydzcosα=dxdzcosβ=dxdycosγ=ds
- 法向量{cosα,cosβ,cosγ}有上下两侧之分,具体见第二类曲面的∑朝上还是朝下
-
-
题型
-
归纳
-
为什么线面积分可代入,重积分不可代入
例:二重积分∬Dx2+y2dσ,D:x2+y2<=1
注意到二重积分的定义区间为x2+y2<=1,故平面内的大部分点不满足定义区间公式x2+y2=1
-
二型线面积分
- 奇偶性:慎用,逆奇偶性容易用错
- 轮换对称性:要求苛刻,直接忽略
-
格林公式,斯托克斯公式与高斯公式
基本原理:牛顿-莱布尼兹公式在高维的扩展
关系:
-
斯托克斯公式:由三维空间一型线积分,通过旋度公式,向一/二型面积分转化
方向:逆时针向上
-
格林公式:是斯托克斯公式在XoY平面的反映
方向:逆时针为正
-
高斯公式:有三维空间二型面积分,通过散度公式,向三重积分转化
方向:向外为正
-
-
若被积函数为一元,如z
-
若积分区域对称:奇偶性(平移)
-
若积分区域规则:形心公式∬Dxyxdσ=ˉx∬Dxydσ
注:ˉx通常在规则曲面的中心
-
-
若积分区域函数(三重积分,一线,二线,一面,二面稍有不同)为x2+y2+z2=R2,被积函数为(x+y+z)2
显然(x+y+z)2=x2+y2+z2+2xy+2xz+2yz
- 由奇偶性
- 三重积分,一线,一面:2xy,2xz,2yz积分为0
- 二线,二面:偶函数x2,y2,z2积分为0
- 由代入性质(一线,一面):x2+y2+z2=R2
- 由奇偶性
-
计算的一般流程:线面积分 => 重积分 => 累次积分
注:这样出题也会显得有深度
-
-
计算三重积分
使用
-
考察积分区间:若积分区间对称,则被积函数可以使用奇偶性,轮换对成性
-
考察被积函数:
-
奇偶性
-
轮换对称性:使被积函数能通过积分区间化简
-
可以是任意两个变量具有轮换对称性
例:I=∭Ωx2dv,Ω:{x2+y2+z2<=1z>0
I关于x,y具有轮换对称性,显然I=∭Ωx2dv=∭Ωy2dv
-
化简计算
如I=∭Ωx2+y2dv,其中Ω:x2+y2+z2
则I=∭Ω2x2dv=∭Ω23(x2+y2+z2)dv
-
-
使用积分区间区间化简
-
-
化为累次积分
-
含x2+y2:极坐标系
-
可切面:先二(重积分)后一
-
可穿针:先一后二(重积分)
例:∭Ω2zdv,Ω:x2+y2=1,z=1−x所围区域,
- 找到一个较为简单的投影平面:Dxy:x2+y2<=1
- 消去另一个变量,对该变量使用穿针法确定上下平面:显然应该消去另一个变量z,用穿针法可得对应上下平面为z1=0,z2=1−x
- 代入有:∬Dxydσ∫1−x02zdz
-
-
含x2+y2+z2:球坐标系
-
-
-
三元累次积分交换次序:降维看问题,两两对换
例:I=∫10dx∫x0dy∫xzf(z)dz
- 先将x看做常数,交换yoz平面的积分顺序
- 再交换xoz平面的积分顺序
-
线面积分的直接法:重点在于微元ds的处理,积分区间L或∑的转化
-
一型线积分:直接代入ds=√y′2t+x′2tdt
一型空间线积分:转化为参数方程dS=√x′2(t)+y′2(t)+z′2(t)dσ
例:{x2+y2+z2=R2x+y+z=0
消元:z=−x−y,32x2+2(y+x2)2=R2
则有{x=√23Rcosθy=R√2sinθ−R√6cosθz=−R√2sinθ−R√6cosθ
-
二型线积分:转为一重线积分
公式:∫LPdx+Qdy=∫βα[P(x(t),y(y))x′t+Q(x(t),y(t))y′t]dt
二型空间线积分:
设L:{x=x(t)y=y(t),t∈[α,β],则
∫LPdx+Qdy=∫βα[P(x(t),y(t))x′(t)+Q(x(t),y(t))y′(t)]dt
-
一型面积分:直接代入dS=√1+z2x+z2ydσ
-
二型面积分:转为二重积分
- Σ=±Dxy
- 若某一变量为常数(如z):对该变量的积分(dz)为0
-
-
计算一型线积分
-
考察积分区间:若对称,则可以考虑对被积函数使用奇偶性,轮换对成性
-
考察被积函数:
-
利用奇偶性
-
利用轮换对称性
-
积分区域代入:考察积分区域与被积函数,可结合轮换对称性
例:L:x2+y2+z2=1,x+y+z=0交线,求∮Lxyds
考虑到(x+y+z)2=x2+y2+z2+2xy+2xz+2yz
故I=16∮(x+y+z)2−(x2+y2+z2)ds
-
-
-
计算对坐标的线积分
基本思路
-
曲线曲面积分考虑代入化简
-
考察格林公式的使用条件
-
考虑被积函数定义区间
-
注意外逆内顺,根据被积函数的定义区间补线
半椭圆补线:
例:∫cxdy+ydxx2+y2,c:y24+y29=1(y>0),逆时针
注意到(0,0)点为被积函数的无定义点,为了方便消去x2+y2,可在上方补线x2+y2=9(y>0)
-
-
路径无关:∂P∂y=∂Q∂x
-
原函数简单:找原函数
-
原函数复杂:改换路径
当L为包含原点的逆时针封闭曲线,取L1为逆时针且可以方便消去分母的封闭曲线
-
I=∫L1xdx−ydyx2+y2
-
I=∫L1xdy−ydx4x2+y2
注:因为4x2+y2−8x2=−(4x2+y2−2y2)
-
I=∫L1(x−y)dx−(x+y)dyx2+y2
-
I=∫L1(x+y)dx−(x−y)dyx2+y2
-
-
-
路径相关:补线为封闭曲线用格林∬D∂Q∂x−∂P∂ydσ
注:
- 通过Pdx+Qdy确定P,Q,进而有∂Q∂x−∂P∂y
- 一般计算简单
路径无关在题目中的表达
-
∫(a2,b2)(a1,b1)Pdx+Qdy:题目中给了点但没有路径曲线,说明路径无关
-
结合图像证路径无关:严选题30题
黄,绿为任意两条路径,I在任意封闭路径内积分相同
注:I在经过黄蓝,黄绿的封闭曲线上积分相同,则I对于A到B的积分与路径无关
使用不等式:格林公式转化为二重积分
空间二型线积分:
-
积分区域的是曲面和平面的交线:空间线积分化为平面线积分 => 格林公式
∮LPdx+Qdy+Rdz且z=f(x,y)
- dz=f′xdx+f′ydy
- 在P,Q,R中代入z=f(x,t)
-
封闭空间:使用斯托克斯公式
注:方向使用右手法则
补线¯AB:表示由A到B的直线
-
-
计算对面积的面积积分
-
考察积分区域:是否具有对称性
-
考察被积函数
- 奇偶性
- 轮换对成性
- 直接代入法:在轮换后用直接代入
-
降维
-
转化为定积分
例:∑:x2+y2=R2,0<=z<=H
由题,令dS=2πdz
-
转化为一型线积分
例:∑:圆柱面(x−1)2+y2=1介于平面z=0与上半圆锥面z=√x2+y2之间部分的面积
由题,令dS=zds
注:前面的dS表示面积分,后面的ds表示线积分
-
-
-
计算对坐标的面积积分
方法
-
考察被积函数:是否可以使用积分区域化简
-
通过求导化简被积函数
- 高斯公式
- 第一,二类曲面积分的关系公式
-
一型面积分与二型面积分的关系
-
轮换对称性,反奇偶性(实际上用得比较少)
例:∬sz+z2dxdyx2+y2+z2,S:x2+y2=R2,z=R,z=−R,取外侧
令S1为上面,S2为下面
- 对于奇函数z:∬szdxdyx2+y2+z2=∬s1Rdxdyx2+y2+R2−∬s2(−R)dxdyx2+y2+R2=2∬s12Rdxdyx2+y2+R2
- 对于偶函数z2:∬sz2dxdyx2+y2+z2=∬s1R2dxdyx2+y2+R2−∬s2(−R)2dxdyx2+y2+R2=0
-
-
多元积分的应用
-
转动惯量:Ix=∬Dy2ρ(x,y)dσ
注:y2表示的是距离的平方
-
题型
-
求几何量
求柱面:可以使用线积分
∑:x2+y2=a2,0<=z<=x
则有S=∫Lzds
-
计算物理量
做功:关键是找到F的向量表示→F={P,Q}
则I=∫LPdx+Qdy
-
场论初步
-
梯度(函数 => 向量)
有函数u=f(x,y,z)
gradu=∂u∂x→i+∂u∂y→j+∂u∂z→k
-
散度(向量 => 函数)
有向量场A(x,y,z)={P,Q,R}
divA=∂P∂x+∂Q∂y+∂R∂z
-
旋度(向量 => 向量)
有向量场A(x,y,z)={P,Q,R}
rotA=|ijk∂∂x∂∂y∂∂zPQR|
注:P,Q,R函数方程写在最下方
-
正项数列an单调减少 => liman存在
注:因为an>0
-
分解分数因式
例:1n2−1
显然两个因子分别为n−1,n+1
而1=[(n+1)−(n−1)]∗12
故可分解因式为1n−1−1n+1
-
函数定义域的变化
-
解微分方程
例:f(0)=0,xf′(x)=x
则有g(x)=x+c(x≠0)
令g(0)=0,则c=0
故,f(x)=x
-
级数展开
例:f(x)={sinxx,x≠01,x=0
g(x)=sinxx=∑∞n=0(−1)n(2n+1)!x2n+1(x≠0)
而g(0)=1(x≠0)
故f(x)=g(x)(x∈R)
-
-
定积分
an=∫nπ0x\abssinxdx=nπ2∫nπ0\abssintdt
-
limn→∞(a12+...+an2n):也可以看做级数,故级数也是求和式极限的一种方法
-
向量计算
设A为起点,B为终点
尝试将A移到原点位置
故→AB=B−A
-
lim(x,y)→(0,0)√x2+y2
=lim(x,y)→(0,0)x2+y2√x2+y2
=lim(x,y)→(0,0)x2√x2+y2+lim(x,y)→(0,0)y2√x2+y2
<=lim(x,y)→(0,0)x√x2+y2∗x+lim(x,y)→(0,0)y√x2+y2∗y
<=lim(x,y)→(0,0)x+lim(x,y)→(0,0)y
=0
-
dz=Adx+Bdy:前提是可微
-
导数定义还可以写做:f′x(x0)=limx→x0f(x)−f(x0)\absx−x0
-
单元重概念,多元重计算
-
重积分与累次积分的区别
- 以二重积分为例,其定义的微元是ds
- 显然这是无法计算,但是当被积函数可以通过两个变量x,y(θ,r)定义,我们也可以将ds拆成两个微元的计算,如ds=dxdy=rdθdr,此时可以化为多个定积分的计算,即累次积分
-
轮换对成性下x2+y2与x2+y2+z2的关系
I=26(x2+y2+y2+z2+z2+x2)=26∗2∗(x2+y2+z2)=23(x2+y2+z2)
或者
I=2x2=23(x2+y2+z2)
-
双纽线
(x2+y2)2=a2(x2−y2)
注:适合用极坐标有r2=a2cos2θ
-
等边三角形面积公式:s=√34a2
-
球面积:S=4πR2
-
二阶混合偏导数连续
定理:若f(x,y)的两个二阶混合偏导数fxy(x,y)以及fyx(x,y)在区域D内连续,则该区域内这两个二阶偏导数必相等
-
易错积分区域
-
x2+y2+z2<=R2,x2+y2+z2<=2Rz
-
z=1−x2−y2
即1−z=x2+y2,显然是偏移的旋转抛物面
-
x2+(y−z)2=(1−z)2(0<=z<=1)
当z=0,有x2+y2=1
当z=1,有x2+(y−1)2=0
-
整理
- 研究一个函数
- 定义域和值域
- 单调性,奇偶性,周期性
- 可导性,可积性
- 数列收敛与级数收敛
- 级数收敛是数列的和的收敛
- 数列收敛,级数不一定收敛;级数收敛,数列一定收敛(an=Un−Un−1)
- 数列收敛是单调的,级数收敛是摇摆的
- 有定义
- 连续
- 间断
补充
-
相等与恒等
- 相等:在一定条件下的相等
- 恒等:无条件的相等,这个时候通常可以代入特殊值用特殊求一般
-
同样的思路去理解积分:积分就是类似面积 => 通过中间点求 => 通过极限减小误差
-
积分中默认下限小于上限,f(x)>0 => 此时才能说定积分的几何意义是面积
奇函数的原函数为偶函数(奇函数为f(x),原函数使用∫x0f(x)dt,其它原函数为∫x0f(x)dt+C)
-
右侧:∫b0f(x)dt=s(设s为f(x)在0到b上的面积)
-
左侧:∫a0f(x)dt=−∫0af(x)dt=−(−s)=s
易错:
- 积分下限不变仍然是0
- 由于∫0af(x)dt可以看做无数片的dt∗f(x),而f(x)<0,故这里最终的结果为-s
-
-
积分限变化
F(x)=∫x0f(t+T)dt+C=∫x+TTf(t)dt+C
注:可以看到f(x)中的上下界限始终为T到x+T
-
Lagrange定理
- 形式:f(x2)−f(x1)=f′(ξ),x1<ξ<x2(ξ国际音标读作kxi)
- 使用条件:由于f′(θ)无法确定,通常当f′(x)上任意一点都满足某条件时使用
-
Taylor公式
- 偶函数:只有偶此项,如:cosx=1−12x2+124x4...
- 奇函数:只有奇此项,如:sinx=x−16x3+180x5...
-
洛必达法则:
- 需连续可导 => 转而考虑极限定义
- 可以用于无穷大
证明(尝试通过Lagrange中值定理)
- 已知:f(x)→0,g(x)→0,f(x),g(x)可导(对应洛必达使用法则中的先代后求)
- 证明:
- 由f(x),g(x)可导,故f(x0)=g(x0)=0,原式=limf(x)−f(x0)g(x)−g(x0)
- 由Lagrange定理,上式=limf′(x)g′(x)
-
积分与奇偶性
-
偶函数:积分区间相同
∫a−af(x)dx=2∫a0f(x)dx
-
奇函数:积分区间相差一个负号
∫a−af(x)dx=0
-
-
积分中值定理扩展
若f(x)在(a,b)上连续,则有∫baf(x)g(x)dx=f(ξ)∫bag(x)dx
注:本质上是由连续保证了有这样一个ξ存在
-
不同概念的成立条件:以limx→1f(x)lnx=1为例
- 天然成立:limx→1f(x)=0
- 若f(x)连续:f(1)=0
- 若f(x)可导:limx→1f′(x)=1
-
无穷大比较(趋向无穷的速度):幂函数>>对数函数
-
不同概念的成立条件:以limx→1f(x)lnx=1为例
- 天然成立:limx→1f(x)=0
- 若f(x)连续:f(1)=0
- 若f(x)可导:limx→1f′(x)=1
-
曲线有共同的切线和相切
- 有共同的切线:两曲线在不同点的切线相同
- 相切:在交点处的导数相同
-
积分中φ(u)>0条件使用
sinx−∫yxφ(u)du=0 => y(0)=0
-
还是容易算错
- limx→∞arctanx=π2
- limx→1arctanx=π4
-
arctanx+arctan1x=π2
-
定义域分析的作用
设f(x)在[a,b]上连续,在(a,b)内可导,f(a)=b,f(b)=a,a与b同号,求证:∃ξ∈(a,b),使f′(ξ)=−f(ξ)ξ
构造原函数:F(x)=xf(x)
计算得f′(ξ)ξ+f(ξ)=0,由于题目中a与b同号,故可转化为f′(ξ)=−f(ξ)ξ形式
-
柯西定理和拉格朗日中值定理(几何意义)构造辅助函数,以及是怎样简化的,可以参考视频9
-
积分中值定理:∫baf(t)dt=A,则∃c∈(a,b),使得(b−a)f(c)=A
-
常数判断
- 导数为0
- 代入某个点
-
奇偶性判断
-
对于f(x)=esinxsinx
由于f(−x)=−e−sinxsinx,故f(x)不是奇函数
-
-
直角坐标与极坐标的关系
- {x=rcosθy=rsinθ
- r=√x2+y2
-
点(x0,y0)到直线ax+by+c=0距离
d=ax0+by0+c√a2+b2
-
排除法使用:当选择填空出现一般函数,一般参数时
-
质心与形心
-
质心:质量的中心
一维:¯x=∫baxρ(x)dx∫baρ(x)dx
二维:¯x=∬Dxρ(x,y)dσ∬Dρ(x,y)dσ
-
形心:几何的中心
一维:¯x=b+a2
二维:¯x=∬Dxdσs
-
关系:当密度ρ为常数时,形心即质心
-
-
右手螺旋法则
- 逆时针:向上
- 顺时针:向下



【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 分享4款.NET开源、免费、实用的商城系统
· 全程不用写代码,我用AI程序员写了一个飞机大战
· MongoDB 8.0这个新功能碉堡了,比商业数据库还牛
· 白话解读 Dapr 1.15:你的「微服务管家」又秀新绝活了
· 上周热点回顾(2.24-3.2)