[学习笔记]Border&Period杂谈
十分简要地胡乱说一些与 Border 相关的东西。
Border 是什么？
用 kmp 求的那个东西就是 border，因此 border 可以在 \(\mathcal O(n)\) 内用 kmp 求出来，每个前缀的 border 构成树形结构，把这个树建出来，我们称其为失配树。
Border 的性质
弱周期引理(Weak Periodicity Lemma,WPL)
若 \(p,q\) 为 \(S\) 的周期，且 \(p+q\le |S|\)，那么 \(\gcd(p,q)\) 也是 \(S\) 的周期。
证明：不妨设 \(p<q\)，令 \(d=q-p\)，那么：
- 当 \(i<q\) 时，\(S[i]=S[i+q]=S[i+q-p]=S[i+d]\)；
- 当 \(i>p\) 时，\(S[i]=S[i-p]=S[i-p+q]=S[i+d]\)；
不难发现 \(i\) 取遍 \([1,|S|]\)，因此 \(d\) 也为 \(S\) 的周期，根据辗转相除法，可证 \(\gcd(p,d)\) 为 \(S\) 的周期。
周期定理(Periodicity Lemma,PL)
若 \(p,q\) 为 \(S\) 的周期，且 \(p+q-\gcd(p,q)\le |S|\)，那么 \(\gcd(p,q)\) 也是 \(S\) 的周期。
它比 WPL 稍微强一点在于对 \(p,q\) 的限制。用得少，不证它了。
前缀整除周期传递性
若 \(S\) 是 \(T\) 的前缀，且 \(T\) 有周期 \(a\)，\(S\) 有周期 \(b\)，\(b\mid a\land |S|\ge a\)，则 \(T\) 也有周期 \(b\).
证明：画个图就行。
长串等差匹配位
若 \(2|S|\ge |T|\)，则 \(S\) 在 \(T\) 中的匹配位置必为等差序列.
证明：先将 \(T\) 中没有被 \(S\) 覆盖的部分去掉，由于 \(2|S|\ge |T|\)，因此此时的 \(T\) 的所有部分都被 \(S\) 覆盖。
对于 \(S\) 在 \(T\) 中的匹配位小于等于 \(2\)，结论是显然的，下面考虑匹配位大于 \(2\) 的情况。
设 \(S\) 在 \(T\) 中第一二次的匹配位差为 \(d\)，第二次与后面的某一次匹配位差为 \(q\)，不难发现 \(d,q\) 均为 \(S\) 的周期，并且显然有 \(d+q+|S|\le |T|\)，并且 \(2|S|\ge |T|\)，可得 \(d+q\le |S|\)，由 WPL 得 \(r=\gcd(d,q)\) 为 \(S\) 的周期。设 \(p\) 为 \(S\) 的最小周期，那么有 \(p\mid r\)，否则 可以使用 WPL 构造更小的周期。此时 \(p\mid r\mid d\).
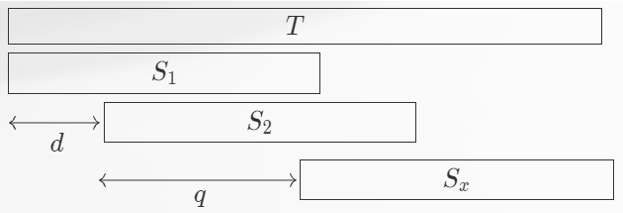
若 \(p<d\)，那么，由于 \(p\) 是 \(S\) 的循环，因此我们可以找到一个距离第一匹配位距离比 \(d\) 更小的第二匹配位，与 \(d\) 的定义矛盾。
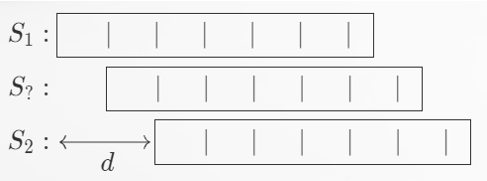
因此只有可能是 \(p=r=d\)，又因为 \(r=\gcd(d,q)=d\)，因此 \(d\mid q\)，所以匹配位在处理之后的 \(T\) 上，从位置 \(1\) 开始，每 \(d\) 个出现一次。还原到原来的 \(T\) 串上，匹配位就是公差为 \(d\) 的等差数列了。
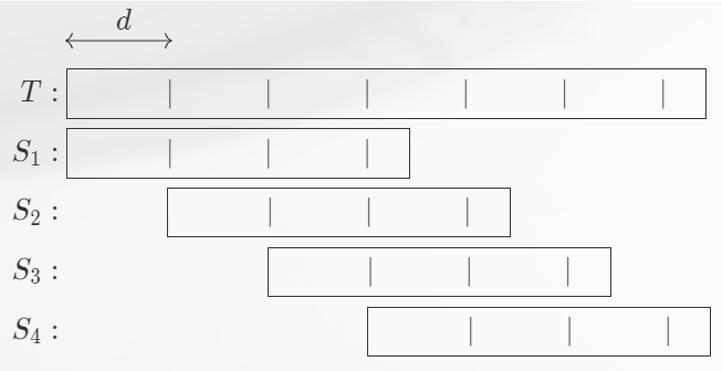
长 border 等差匹配位
\(S\) 的长度达到 \(\displaystyle \frac{n}{2}\) 的 border 的长度构成等差序列。
设 \(n-p,n-q\) 为 \(S\) 的两个长度达到 \(\displaystyle \frac{n}{2}\) 的 border，且 \(n-p\) 是最大的 border，那么 \(p\) 为 \(S\) 的最小周期，且 \(p,q\) 均为 \(S\) 的周期，由于 \(\displaystyle n-p>n-q\ge \frac{n}{2}\)，因此 \(p+q\le n\)，因此 \(r=\gcd(p,q)\) 也为 \(S\) 的周期，由于 \(p\) 是 \(S\) 的最小周期，因此 \(r=p\)，即 \(p\mid q\)，且 \(p\) 是最小周期，因此所有的 border 长度以 \(p\) 为公差构成等差序列。
不难发现，实际上 \(n-kp\) 都是 \(S\) 的 border，因为既然 \(p\) 为周期，那么 \(2p,3p,\cdots\) 均为周期，进而说明 \(n-2p,n-3p,\cdots\) 均为 border.
长 border 大一统
设 \(n-p\) 为 \(S\) 的最大 border，如果 \(\displaystyle n-p\ge \frac{n}{2}\)，那么所有 \(S\) 的长度在 \([p,n-p]\) 的 border 都是 \(n-kp\) 的形式，并且不存在其他形式。
采用反证法，设 \(n-r\) 也是长度在 \([p,n-p]\) 的 border，且不是 \(n-kp\) 的形式。由于 \(p\) 也是周期，因此我们显然可以将这个 \(r\) 进行 \(\pm p\) 来任意调整。
假设 \(r\in [kp,(k+1)p)\)，显然我们可以找到一个 \(q\in [kp,(k+1)p)\) 且 \(p\mid q\)，此时，如果 \(r+q\le n\)，那么我们就可以使用 WPL 证明 \(d=\gcd(r,q)\le |r-q|<p\) 为周期进而推出矛盾了。
如何达到 \(r+q\le n\) 呢？注意前面，我们可以将 \(r\) 进行调整，显然可以将 \(r\) 对 \(\displaystyle p\le \frac{n}{2}\) 取模，此时保证了 \(\displaystyle r<\frac{n}{2}\)，此时 \(r+q\le n\) 了。
当然也可以用前面的等差匹配位来证明，显然可以找到一个 \(t\) 使得 \(\displaystyle n-r+tp\ge \frac{n}{2}\)，且 \(n-r+tp\) 也为 border，由等差匹配位，\(n-r+tp\) 应与其他 \(n-kq\) 构成等差序列，此时公差会变小，与 \(p\) 的假设构成矛盾。
等差数列对数级
一个串 \(S\) 的所有 border 按长度排序后，可以被划分成 \(\mathcal O(\log n)\) 个等差序列。
把达到 \(\displaystyle \frac{n}{2}\) 的 border 取出来，就是一个等差序列。然后只需要考虑长度为 \(\displaystyle \frac{n}{2}\) 的前缀 \(S'\)，对于 \(S'\)，将达到 \(\displaystyle \frac{n}{4}\) 的 border 取出来，又是一个等差序列......因此，只会有 \(\mathcal O(\log n)\) 个等差序列。
