[题解]物理学科竞赛
\[\color{red}{\text{校长者,真神人也,左马桶,右永神,会执利笔破邪炁,何人当之?}} \\
\begin{array}{|}
\hline
\color{pink}{\text{The principal is really a god}} \\
\color{pink}{\text{with a closestool on the left and Yongshen on the right}} \\
\color{pink}{\text{holding a sharp pen to pierce the truth}} \\
\color{pink}{\text{Who can resist him? }} \\
\hline
\end{array} \\
\begin{array}{|}
\hline
\color{green}{\text{校長は本当に神であり、左側にトイレ、右側にヨンシェンがあり}} \\
\color{green}{\text{鋭いペンを持って真実を突き刺している。誰が彼に抵抗できるだろうか? }} \\
\hline
\end{array} \\
\begin{array}{|}
\hline
\color{lightblue}{\text{Le principal est vraiment un dieu}} \\
\color{lightblue}{\text{avec des toilettes à gauche et Yongshen à droite}} \\
\color{lightblue}{\text{tenant un stylo pointu pour percer la vérité}} \\
\color{lightblue}{\text{Qui peut lui résister ? }} \\
\hline
\end{array} \\
\begin{array}{|}
\hline
\color{purple}{\text{Der Direktor ist wirklich ein Gott}} \\
\color{purple}{\text{mit einer Toilette links und Yongshen rechts}} \\
\color{purple}{\text{der einen spitzen Stift hält}} \\
\color{purple}{\text{um die Wahrheit zu durchdringen.}} \\
\color{purple}{\text{Wer kann ihm widerstehen? }} \\
\hline
\end{array} \\
\begin{array}{|}
\hline
\color{cyan}{\text{Principalis deus est, Yongshen a dextris cum latrina}} \\
\color{cyan}{\text{acuto stylo ad perforandum veritatem: quis resistet ei? }} \\
\hline
\end{array} \\
\color{red}{\text{对曰:“无人,狗欲当之,还请赐教!”}} \\
\newcommand\brak[1]{\left({#1}\right)}
\newcommand\Brak[1]{\left\{{#1}\right\}}
\newcommand\d[0]{\text{d}}
\newcommand\string[2]{\genfrac{\{}{\}}{0pt}{}{#1}{#2}}
\newcommand\down[2]{{#1}^{\underline{#2}}}
\newcommand\ddiv[2]{\left\lfloor\frac{#1}{#2}\right\rfloor}
\newcommand\udiv[2]{\left\lceil\frac{#1}{#2}\right\rceil}
\newcommand\lcm[0]{\operatorname{lcm}}
\newcommand\set[1]{\left\{{#1}\right\}}
\newcommand\ceil[1]{\left\lceil{#1}\right\rceil}
\newcommand\floor[1]{\left\lfloor{#1}\right\rfloor}
\newcommand\rhs[1]{\;\text{Rhs}\;#1}
\newcommand\lhs[1]{\;\text{Lhs}\;#1}
\newcommand\Vec[1]{\vec{\mathbf{#1}}}
\newcommand\rank[0]{\text{rank}}
\]
\(\mathcal{Back\;To\;The\;Menu}\).
2022-02-25 物理学科竞赛
小说 / Novel
目前没人做出来,也没有题解,我也不会做。
LJJ的电阻网络 / Grid
还去专门请问了我们的物理老师。
先看一看 \(x=y\) 的情况,它十分良心地给了我们一个公式:
\[R=\frac{2}{\pi}\sum_{i=1}^n \frac{1}{2i-1}
\]
结果这个部分分就变成推柿子了......涉及欧拉函数,我觉得可能考场上没人可以做出来......题解推得很清楚,可以去看看题解。
我们可以设从 \((0,0)\) 导入了大小为 \(I\) 的电流,那么网格中的所有电流都是以 \((0,0)\) 为原点中心对称的,举个例子:
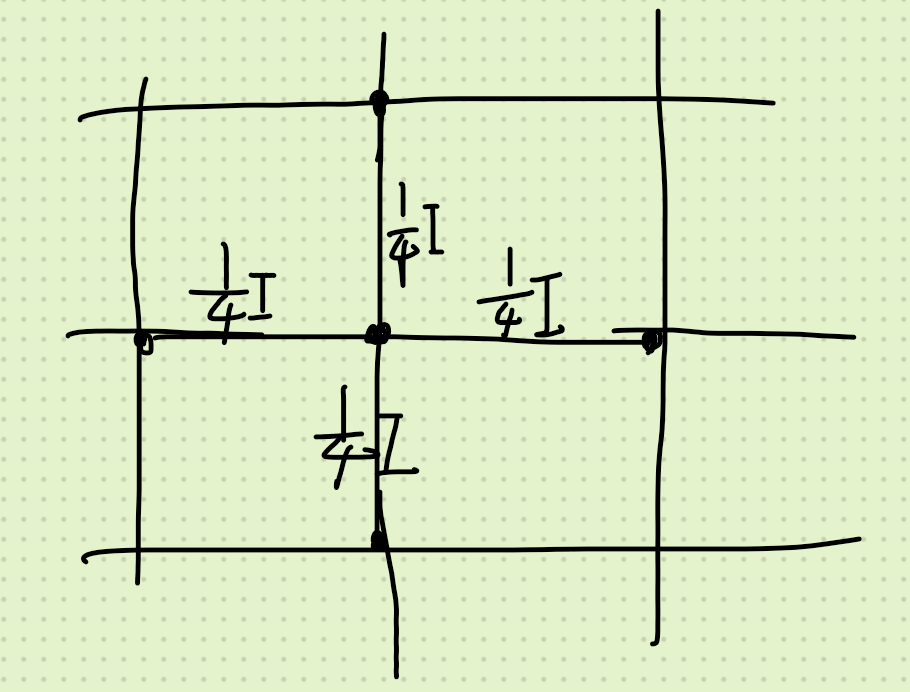
中间那个点是 \((0,0)\).
实际上,在 \((0,0)\) 处导入电流之后,就从它开始按照上面这样发散,流向无穷远,它显然符合基尔霍夫定律的。
做个类比,如果我们不在 \((0,0)\) 导入电流,而在 \((x,y)\) 导出 \(I\) 的电流,那么图上的电流也类似上图,从无穷远处,以 \((x,y)\) 为原点对称,流向 \((x,y)\),最后流出 \(I\),它也符合基尔霍夫定律。
原题目,实际上就是这两种效果的叠加,由于输入输出都符合基尔霍夫定律,叠加也一定符合。
剩下,就可以去看题解了(并不是我懒,而是时间不够了)
祖先 / Ancestor
唯一一个有代码的......
考虑使用 DDP 的思路,先重剖,然后分开维护轻儿子和重儿子即可,可能每次增量会有一些变化量和需要维护的辅助变量,可以自己推一下。我写的复杂度是 \(\mathcal O(n\log ^2 n)\).
/** @author __Elaina__ */
#include <bits/stdc++.h>
using namespace std;
// #define USING_FREAD
// #define NDEBUG
#include <cassert>
namespace Elaina {
/** その可憐な少女は魔女であり、旅人でした。 ―― そう、私です! */
#define rep(i, l, r) for(int i = (l), i##_end_ = (r); i <= i##_end_; ++i)
#define drep(i, l, r) for(int i = (l), i##_end_ = (r); i >= i##_end_; --i)
#define fi first
#define se second
#define mp(a, b) make_pair(a, b)
#define Endl putchar('\n')
#define whole(v) ((v).begin()), ((v).end())
#define bitcnt(s) (__builtin_popcount(s))
/** @warning no forced type conversion */
#define rqr(x) ((x) * (x))
#define y0 FUCK_UP
#define y1 MOTHER_FUCKER
typedef long long ll;
typedef unsigned long long ull;
typedef std::pair<int, int> pii;
template<class T> inline T fab(T x) { return x < 0 ? -x : x; }
template<class T> inline void chkmin(T& x, const T rhs) { x = std::min(x, rhs); }
template<class T> inline void chkmax(T& x, const T rhs) { x = std::max(x, rhs); }
#ifdef USING_FREAD
inline char qkgetc() {
# define BUFFERSIZE 1 << 20
static char BUF[BUFFERSIZE], *p1 = BUF, *p2 = BUF;
return p1 == p2 && (p2 = (p1 = BUF) + fread(BUF, 1, BUFFERSIZE, stdin), p1 == p2) ? EOF : *p1++;
# undef BUFFERSIZE
}
# define CHARRECEI qkgetc()
#else
# define CHARRECEI getchar()
#endif
template<class T> inline T readret(T x) {
x = 0; int f = 0; char c;
while (!isdigit(c = CHARRECEI)) if(c == '-') f = 1;
for (x = (c ^ 48); isdigit(c = CHARRECEI); x = (x << 1) + (x << 3) + (c ^ 48));
return f ? -x : x;
}
template<class T> inline void readin(T& x) {
x = 0; int f = 0; char c;
while (!isdigit(c = CHARRECEI)) if (c == '-') f = 1;
for (x = (c ^ 48); isdigit(c = CHARRECEI); x = (x << 1) + (x << 3) + (c ^ 48));
if (f) x = -x;
}
template<class T, class... Args> inline void readin(T& x, Args&... args) {
readin(x), readin(args...);
}
template<class T> inline void writln(T x, char c = '\n') {
if (x < 0) putchar('-'), x = -x;
static int __stk[55], __bit = 0;
do __stk[++__bit] = x % 10, x /= 10; while (x);
while (__bit) putchar(__stk[__bit--] ^ 48);
putchar(c);
}
} // namespace Elaina
using namespace Elaina;
const int Maxn = 2e5;
int n, q, val[Maxn + 5];
vector<int> g[Maxn + 5];
int fa[Maxn + 5];
inline void input() {
readin(n, q);
rep (i, 2, n) readin(fa[i]), g[fa[i]].push_back(i);
rep (i, 1, n) readin(val[i]);
}
int siz[Maxn + 5], wson[Maxn + 5];
void dfs1(int u) {
siz[u] = 1;
for (const int& v: g[u]) {
dfs1(v), siz[u] += siz[v];
if (siz[v] > siz[wson[u]]) wson[u] = v;
}
}
int tp[Maxn + 5], dfn[Maxn + 5], nde[Maxn + 5], qr[Maxn + 5];
ull lsq[Maxn + 5];
void dfs2(int u) {
dfn[u] = ++*dfn, nde[*dfn] = u;
if (wson[u]) {
tp[wson[u]] = tp[u]; dfs2(wson[u]);
for (const int& v: g[u]) if (v ^ wson[u])
dfs2(tp[v] = v), lsq[u] += 1ull * siz[v] * siz[v];
}
qr[u] = *dfn;
}
/** @brief used to maintain the sum of the tree */
namespace sgtre {
ull sum[Maxn << 2 | 2], tag[Maxn << 2 | 2];
#define ls (i << 1)
#define rs (i << 1 | 1)
#define mid ((l + r) >> 1)
#define _lhs ls, l, mid
#define _rhs rs, mid + 1, r
#define _this i, l, r
inline void add(ull d, int i, int l, int r) {
tag[i] += d, sum[i] += d * (r - l + 1);
}
inline void pushdown(int i, int l, int r) {
if (!tag[i]) return ;
add(tag[i], _lhs), add(tag[i], _rhs), tag[i] = 0;
}
inline void pushup(int i) { sum[i] = sum[ls] + sum[rs]; }
void modify(int ql, int qr, ull d, int i = 1, int l = 1, int r = n) {
if (ql <= l && r <= qr) return add(d, _this);
pushdown(_this);
if (ql <= mid) modify(ql, qr, d, _lhs);
if (mid < qr) modify(ql, qr, d, _rhs);
pushup(i);
}
ull query(int ql, int qr, int i = 1, int l = 1, int r = n) {
if (ql <= l && r <= qr) return sum[i];
pushdown(_this); ull ret = 0;
if (ql <= mid) ret += query(ql, qr, _lhs);
if (mid < qr) ret += query(ql, qr, _rhs);
return ret;
}
#undef ls
#undef rs
#undef mid
#undef _lhs
#undef _rhs
#undef _this
} // namespace sgtre;
/** @brief used to maintain the contribution of the light sons */
namespace saya {
ull sum[Maxn << 2 | 2]; ///< the sum of the light sons
ull sqs[Maxn << 2 | 2]; ///< the square sum of the light sons
ull szd[Maxn << 2 | 2]; ///< maintain the value of siz * sum
ull tag[Maxn << 2 | 2];
#define ls (i << 1)
#define rs (i << 1 | 1)
#define mid ((l + r) >> 1)
#define _lhs ls, l, mid
#define _rhs rs, mid + 1, r
#define _this i, l, r
inline void add(ull d, int i, int l, int r) {
if (l ^ r) return void(tag[i] += d);
// fprintf(stderr, "add :> l == r == %d, d == %llu\n", l, d);
int x = nde[l], ws = wson[nde[l]];
// fprintf(stderr, "x == %d, ws == %d\n", x, ws);
// fprintf(stderr, "szd == %llu, lsq == %llu\n", szd[i], lsq[x]);
sqs[i] += szd[i] * d * 2ull + lsq[x] * d * d;
szd[i] += lsq[x] * d;
sum[i] += (siz[x] - siz[ws] - 1ull) * d;
}
inline void pushdown(int i, int l, int r) {
if (!tag[i]) return ;
add(tag[i], _lhs), add(tag[i], _rhs), tag[i] = 0;
}
void modify(int ql, int qr, ull d, int i = 1, int l = 1, int r = n) {
// fprintf(stderr, "ql == %d, qr == %d, d == %llu\n", ql, qr, d);
if (ql <= l && r <= qr) return add(d, _this);
pushdown(_this);
if (ql <= mid) modify(ql, qr, d, _lhs);
if (mid < qr) modify(ql, qr, d, _rhs);
return ;
}
void modipos(int p, ull ds, ull dsq, ull dszd, int i = 1, int l = 1, int r = n) {
if (l == r) {
sum[i] += ds, sqs[i] += dsq, szd[i] += dszd;
return ;
}
pushdown(_this);
if (p <= mid) modipos(p, ds, dsq, dszd, _lhs);
else modipos(p, ds, dsq, dszd, _rhs);
}
ull query(int p, int i = 1, int l = 1, int r = n) {
if (l == r) {
int x = nde[p], ws = wson[nde[p]];
if (!ws) return 0;
// fprintf(stderr, "ws == %d\n", ws);
ull wsum = sgtre::query(dfn[ws], qr[ws]);
ull cur = sgtre::query(l, l);
// fprintf(stderr, "cur == %llu, wsum == %llu\n", cur, wsum);
// fprintf(stderr, "sum == %llu, sqs == %llu\n", sum[i], sqs[i]);
cur *= (wsum + sum[i]) * 2ull; // root & sons
cur += (wsum + sum[i]) * (wsum + sum[i]); // between sons
cur -= sqs[i] + wsum * wsum; // inclusive&exclusive principle
cur >>= 1;
return cur;
}
pushdown(_this);
if (p <= mid) return query(p, _lhs);
return query(p, _rhs);
}
#undef ls
#undef rs
#undef mid
#undef _lhs
#undef _rhs
#undef _this
} // namespace saya;
inline void update(int u, ull d) {
for (u = tp[u]; fa[u]; u = tp[fa[u]]) {
ull sum = sgtre::query(dfn[u], qr[u]);
saya::modipos(dfn[fa[u]], d, sum * sum - (sum - d) * (sum - d), d * siz[u]);
}
}
inline void addp(int u, ull d) {
sgtre::modify(dfn[u], dfn[u], d);
update(u, d);
}
inline void addt(int u, ull d) {
sgtre::modify(dfn[u], qr[u], d);
saya::modify(dfn[u], qr[u], d);
update(u, d * siz[u]);
}
signed main() {
// freopen("samples//ex_ancestor2.in", "r", stdin);
// freopen("samples//ancestor.out", "w", stdout);
// freopen("err_file.out", "w", stderr);
freopen("ancestor.in", "r", stdin);
freopen("ancestor.out", "w", stdout);
input(); dfs1(1); dfs2(tp[1] = 1);
rep (i, 1, n) addp(i, val[i]);
char op[5]; int u, d;
while (q--) {
scanf("%s", op);
if (*op == 'Q') {
readin(u);
writln(saya::query(dfn[u]) << 1 >> 1);
continue;
}
readin(u, d);
if (*op == 'S') addp(u, d);
else addt(u, d);
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号