[题解]高级监狱Ⅲ
\[\color{red}{\text{校长者，真神人也，左马桶，右永神，会执利笔破邪炁，何人当之？}} \\
\begin{array}{|}
\hline
\color{pink}{\text{The principal is really a god}} \\
\color{pink}{\text{with a closestool on the left and Yongshen on the right}} \\
\color{pink}{\text{holding a sharp pen to pierce the truth}} \\
\color{pink}{\text{Who can resist him? }} \\
\hline
\end{array} \\
\begin{array}{|}
\hline
\color{green}{\text{校長は本当に神であり、左側にトイレ、右側にヨンシェンがあり}} \\
\color{green}{\text{鋭いペンを持って真実を突き刺している。誰が彼に抵抗できるだろうか？ }} \\
\hline
\end{array} \\
\begin{array}{|}
\hline
\color{lightblue}{\text{Le principal est vraiment un dieu}} \\
\color{lightblue}{\text{avec des toilettes à gauche et Yongshen à droite}} \\
\color{lightblue}{\text{tenant un stylo pointu pour percer la vérité}} \\
\color{lightblue}{\text{Qui peut lui résister ? }} \\
\hline
\end{array} \\
\begin{array}{|}
\hline
\color{purple}{\text{Der Direktor ist wirklich ein Gott}} \\
\color{purple}{\text{mit einer Toilette links und Yongshen rechts}} \\
\color{purple}{\text{der einen spitzen Stift hält}} \\
\color{purple}{\text{um die Wahrheit zu durchdringen.}} \\
\color{purple}{\text{Wer kann ihm widerstehen? }} \\
\hline
\end{array} \\
\begin{array}{|}
\hline
\color{cyan}{\text{Principalis deus est, Yongshen a dextris cum latrina}} \\
\color{cyan}{\text{acuto stylo ad perforandum veritatem: quis resistet ei? }} \\
\hline
\end{array} \\
\color{red}{\text{对曰：“无人，狗欲当之，还请赐教！”}} \\
\newcommand\brak[1]{\left({#1}\right)}
\newcommand\Brak[1]{\left\{{#1}\right\}}
\newcommand\d[0]{\text{d}}
\newcommand\string[2]{\genfrac{\{}{\}}{0pt}{}{#1}{#2}}
\newcommand\down[2]{{#1}^{\underline{#2}}}
\newcommand\ddiv[2]{\left\lfloor\frac{#1}{#2}\right\rfloor}
\newcommand\udiv[2]{\left\lceil\frac{#1}{#2}\right\rceil}
\newcommand\lcm[0]{\operatorname{lcm}}
\newcommand\set[1]{\left\{{#1}\right\}}
\newcommand\ceil[1]{\left\lceil{#1}\right\rceil}
\newcommand\floor[1]{\left\lfloor{#1}\right\rfloor}
\newcommand\rhs[1]{\;\text{Rhs}\;#1}
\newcommand\lhs[1]{\;\text{Lhs}\;#1}
\newcommand\Vec[1]{\vec{\mathbf{#1}}}
\newcommand\rank[0]{\text{rank}}
\]
\(\mathcal{Back\;To\;The\;Menu}\).
2022-02-10 高级监狱 Ⅲ
一般图带权多重匹配 / Match
真的勾八离谱，怎么连这个题都做不来只能说对欧拉路不甚熟悉了。
如果我们将 选择 \(i,j\) 并将 \(a_i,a_j\) 同时减去一并且花费 \(c_{i,j}\) 视作 选择二元组 \((i,j)\) 并在 \(i,j\) 间连一条边。花费为 \(c_{i,j}\)，那么 \(a_i\) 就是最后构成图中，点 \(i\) 的度数。
此时再对原题进行分析。先考虑最简单的情况 —— 当 \(\forall i,2\mid a_i\) 时，最后的图就是一个欧拉图咯，这就是一个边定向问题，而由欧拉图的性质我们一定可以将原图进行环划分，使得最后每个点的 \(deg_{in}=deg_{out}\).
如果 \(\exists i,2\nmid a_i\)，那么存在解的条件是满足上述条件的 \(i\) 有偶数个，那么我们将这些 \(i\) 两两分组，每组里面连一条边（就是奇度点两两分组并连接一条边），然后归约为欧拉图的情况。由于我们对于每个奇度点加了一条边，所以他们的 \(deg_{in}=deg_{out}\) 有一个是虚假的，多了一，这个 \(1\) 可以是入度也可以是出度，那么我们不妨枚举每个奇度点是出度多一还是入度多一，然后用最小费用最大流跑就行了，注意一个小剪枝 —— 出度多一的奇度点和入度多一的奇度点数量相当。最后时间复杂度 \(\mathcal O\brak{{k\choose \frac{k}{2}}\times (\text{complexity of costFlow})}\).
/** @author Arextre */
#pragma GCC optimize(2)
#include <bits/stdc++.h>
using namespace std;
#define USING_FREAD
// #define NDEBUG
// #define NCHECK
#include <cassert>
namespace Elaina {
/** その可憐な少女は魔女であり、旅人でした。 ―― そう、私です! */
#define rep(i, l, r) for(int i = (l), i##_end_ = (r); i <= i##_end_; ++i)
#define drep(i, l, r) for(int i = (l), i##_end_ = (r); i >= i##_end_; --i)
#define fi first
#define se second
#define mp(a, b) make_pair(a, b)
#define Endl putchar('\n')
#define whole(v) ((v).begin()), ((v).end())
#define bitcnt(s) (__builtin_popcount(s))
/** @warning no forced type conversion */
#define rqr(x) ((x) * (x))
#define y0 FUCK_UP
#define y1 MOTHER_FUCKER
#ifdef NCHECK
# define iputs(Content) ((void)0)
# define iprintf(Content, argvs...) ((void)0)
#else
# define iputs(Content) fprintf(stderr, Content)
# define iprintf(Content, argvs...) fprintf(stderr, Content, argvs)
#endif
typedef long long ll;
typedef unsigned long long ull;
typedef std::pair<int, int> pii;
template<class T> inline T fab(T x) { return x < 0 ? -x : x; }
template<class T> inline void chkmin(T& x, const T rhs) { x = std::min(x, rhs); }
template<class T> inline void chkmax(T& x, const T rhs) { x = std::max(x, rhs); }
#ifdef USING_FREAD
inline char qkgetc() {
# define BUFFERSIZE 1 << 20
static char BUF[BUFFERSIZE], *p1 = BUF, *p2 = BUF;
return p1 == p2 && (p2 = (p1 = BUF) + fread(BUF, 1, BUFFERSIZE, stdin), p1 == p2) ? EOF : *p1++;
# undef BUFFERSIZE
}
# define CHARRECEI qkgetc()
#else
# define CHARRECEI getchar()
#endif
template<class T> inline T readret(T x) {
x = 0; int f = 0; char c;
while (!isdigit(c = CHARRECEI)) if(c == '-') f = 1;
for (x = (c ^ 48); isdigit(c = CHARRECEI); x = (x << 1) + (x << 3) + (c ^ 48));
return f ? -x : x;
}
template<class T> inline void readin(T& x) {
x = 0; int f = 0; char c;
while (!isdigit(c = CHARRECEI)) if (c == '-') f = 1;
for (x = (c ^ 48); isdigit(c = CHARRECEI); x = (x << 1) + (x << 3) + (c ^ 48));
if (f) x = -x;
}
template<class T, class... Args> inline void readin(T& x, Args&... args) {
readin(x), readin(args...);
}
template<class T> inline void writln(T x, char c = '\n') {
if (x < 0) putchar('-'), x = -x;
static int __stk[55], __bit = 0;
do __stk[++__bit] = x % 10, x /= 10; while (x);
while (__bit) putchar(__stk[__bit--] ^ 48);
putchar(c);
}
} // namespace Elaina
using namespace Elaina;
const int maxn = (50 << 1) + 2;
const int inf = 0x3f3f3f3f;
int a[maxn + 5], n, sum;
int c[maxn + 5][maxn + 5];
vector<int> v; int cnt;
int S, T;
struct edge { int to, nxt, flow, cost; } e[maxn * maxn * maxn + 5];
int tail[maxn + 5], cur[maxn + 5], ecnt;
inline void add_edge(int u, int v, int f, int c) {
e[ecnt] = edge{ v, tail[u], f, c }; tail[u] = ecnt++;
e[ecnt] = edge{ u, tail[v], 0, -c }; tail[v] = ecnt++;
}
inline void update(int i, int f) {
e[i].flow -= f, e[i ^ 1].flow += f;
}
void buildGraph(int s) {
S = n << 1 | 1, T = n + 1 << 1;
memset(tail + 1, -1, T << 2), ecnt = 0;
rep (i, 1, n) if (a[i] & 1 ^ 1) {
add_edge(S, i, a[i] >> 1, 0);
add_edge(i + n, T, a[i] >> 1, 0);
}
for (int i = 0; i < cnt; ++i) {
int t = s >> i & 1;
add_edge(S, v[i], a[v[i]] + t >> 1, 0);
add_edge(v[i] + n, T, a[v[i]] + (t ^ 1) >> 1, 0);
}
rep (i, 1, n) rep (j, 1, n)
add_edge(i, j + n, inf, c[i][j]);
}
int ans = inf;
int dis[maxn + 5];
queue<int> Q;
bool inq[maxn + 5];
inline bool spfa() {
while (!Q.empty()) Q.pop();
memset(dis + 1, 0x3f, T << 2);
memset(inq + 1, false, T);
dis[S] = 0, inq[S] = true;
Q.push(S);
while (!Q.empty()) {
int u = Q.front(); inq[u] = false; Q.pop();
for (int i = tail[u], v; ~i; i = e[i].nxt) if (e[i].flow) {
v = e[i].to;
if (dis[v] > dis[u] + e[i].cost) {
dis[v] = dis[u] + e[i].cost;
if (!inq[v]) Q.push(v);
}
}
}
return dis[T] != inf;
}
bool vis[maxn + 5];
int dfs(int u, int flow) {
if (u == T) return flow;
vis[u] = true;
int gush = 0, v, ret;
for (int& i = cur[u]; ~i; i = e[i].nxt) if (!vis[v = e[i].to]) {
if (e[i].flow && dis[v] == dis[u] + e[i].cost) {
ret = dfs(v, min(flow - gush, e[i].flow));
assert(ret <= flow);
update(i, ret), gush += ret;
}
}
vis[u] = false;
return gush;
}
inline void Dinic() {
int maxf = 0, minc = 0, ret;
while (spfa()) {
memcpy(cur + 1, tail + 1, T << 2);
ret = dfs(S, inf);
maxf += ret, minc += dis[T] * ret;
}
if (maxf == sum) chkmin(ans, minc);
}
signed main() {
freopen("match.in", "r", stdin);
freopen("match.out", "w", stdout);
readin(n);
rep (i, 1, n) {
readin(a[i]), sum += a[i];
if (a[i] & 1) v.push_back(i), ++cnt;
}
if (cnt & 1) return writln(-1), 0;
sum >>= 1;
rep (i, 1, n) rep (j, 1, n) readin(c[i][j]);
int U = 1 << cnt;
for (int s = 0; s < U; ++s) {
if (__builtin_popcount(s) != (cnt >> 1)) continue;
buildGraph(s);
Dinic();
}
writln(ans);
return 0;
}
排序 / Sort
复杂度玄学，代码感觉很复杂，就不写了。什么勾八垃圾题，真就敢写就能过呗......时间复杂度最劣可能达到 \(\mathcal O(2^kn^2)\)，做什么做啊？
传染 / Infect
淀粉质还能这样吃😅.
考虑一般的暴力做法，从每个点开始，从它向所有它能够覆盖到的点连边以构成新图，最后我们在新图上跑一边 tarjan 之后数一数度数为 \(0\) 的点的个数即可。时间复杂度 \(\mathcal O(n^2)\).
考虑上述算法的劣势在哪里？边数太多了，建图太慢了，两者的级别都是 \(\mathcal O(n^2)\). 我们考虑优化这个过程。
注意到我们实际上有很多被重复考察的东西，比如说，相邻的两个点，他们能够到达的点一定有很多是相同的，但是暴力无法处理到底有哪些点是相同的，这导致效率大大降低了。这里引入一种淀粉质的神奇应用。
考虑点分树，在每个分治中心下，我们处理所有点 跨越分治中心 的覆盖，也就是将每个点归到分治中心上，此时它的半径为 \(r_i-d_i\)，其中 \(d_i\) 表示该点到分治中心的距离，然后我们直接上图：
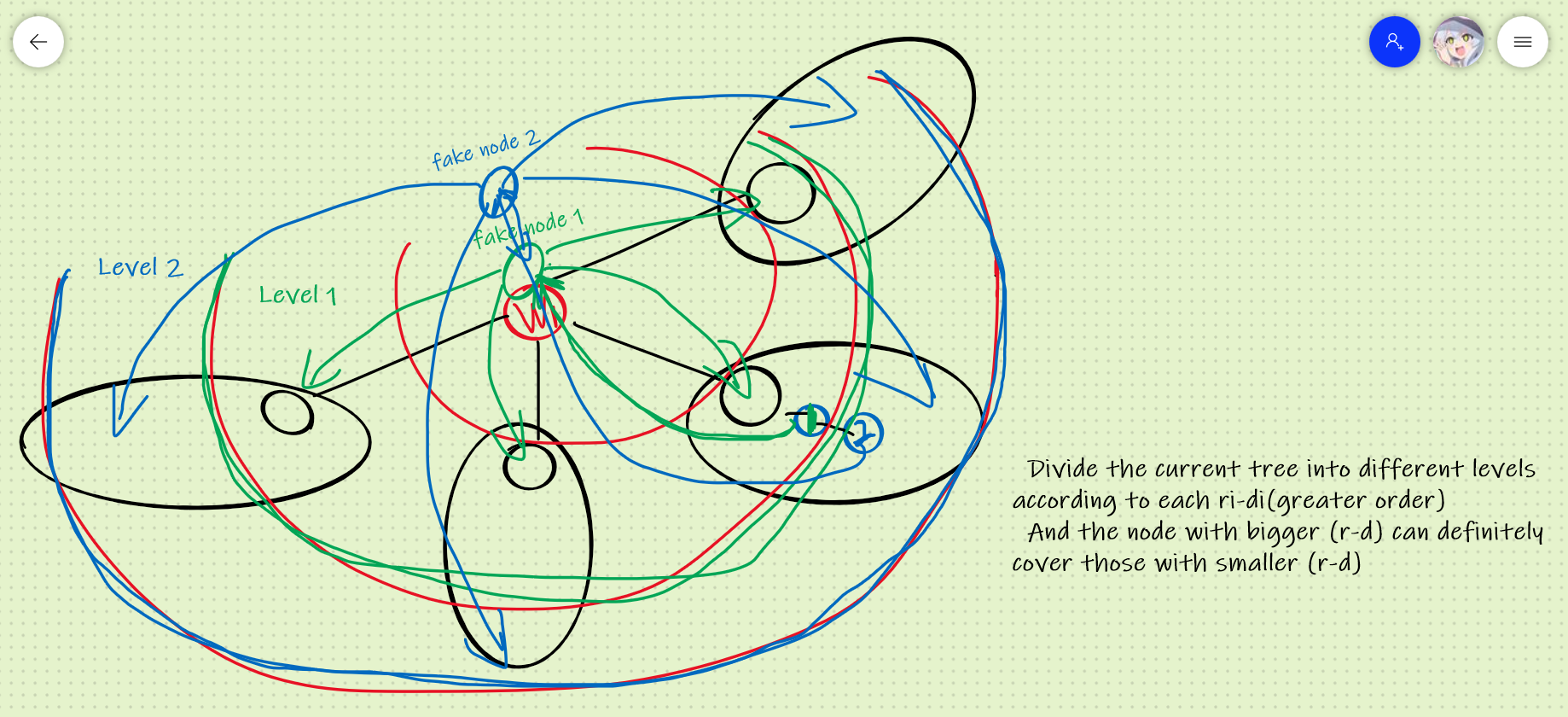
一号点对应在虚点的 fake node 1，二号店对应的虚点是 fake node 2，假设二号点有更大的 \(r-d\)，那么归到分治中心时，一号点能够走到的点二号点也可以走到，所以我们可以直接从 fake node 2 向 fake node 1 连边，表示 继承 其所有可以到达的点，然后再补充那些只属于 Level 2 的点即可。
而子树之内，由于我们每次分治将处理跨越分治中心的点，递归下去将会将所有的覆盖都处理完全，但是我们的 继承 优化了建图，点数只有 \(\mathcal O(n+n\log n)\) 这么多了，最后再跑 tarjan，复杂度可以接受，最终复杂度是 \(\mathcal O(n\log^2 n)\)，因为每次分治要将 \(r-d\) 排序。
然而这个题还有一个性质 —— 贪心选择 \(r\) 更大的。证明是 trivial 的，但是不知道怎么用这个性质，据 \(\sf HandInDevil\)🚽 说祂实现了一个将会利用这个性质的做法，然而假了 😢 .
下面的代码实现写得有点丑，常数稍大。 但是还是可以过 😃
/** @author Arextre */
#include <bits/stdc++.h>
using namespace std;
#define USING_FREAD
// #define NDEBUG
// #define NCHECK
#include <cassert>
namespace Elaina {
/** その可憐な少女は魔女であり、旅人でした。 ―― そう、私です! */
#define rep(i, l, r) for(int i = (l), i##_end_ = (r); i <= i##_end_; ++i)
#define drep(i, l, r) for(int i = (l), i##_end_ = (r); i >= i##_end_; --i)
#define fi first
#define se second
#define mp(a, b) make_pair(a, b)
#define Endl putchar('\n')
#define whole(v) ((v).begin()), ((v).end())
#define bitcnt(s) (__builtin_popcount(s))
/** @warning no forced type conversion */
#define rqr(x) ((x) * (x))
#define y0 FUCK_UP
#define y1 MOTHER_FUCKER
#ifdef NCHECK
# define iputs(Content) ((void)0)
# define iprintf(Content, argvs...) ((void)0)
#else
# define iputs(Content) fprintf(stderr, Content)
# define iprintf(Content, argvs...) fprintf(stderr, Content, argvs)
#endif
typedef long long ll;
typedef unsigned long long ull;
typedef std::pair<int, int> pii;
template<class T> inline T fab(T x) { return x < 0 ? -x : x; }
template<class T> inline void chkmin(T& x, const T rhs) { x = std::min(x, rhs); }
template<class T> inline void chkmax(T& x, const T rhs) { x = std::max(x, rhs); }
#ifdef USING_FREAD
inline char qkgetc() {
# define BUFFERSIZE 1 << 20
static char BUF[BUFFERSIZE], *p1 = BUF, *p2 = BUF;
return p1 == p2 && (p2 = (p1 = BUF) + fread(BUF, 1, BUFFERSIZE, stdin), p1 == p2) ? EOF : *p1++;
# undef BUFFERSIZE
}
# define CHARRECEI qkgetc()
#else
# define CHARRECEI getchar()
#endif
template<class T> inline T readret(T x) {
x = 0; int f = 0; char c;
while (!isdigit(c = CHARRECEI)) if(c == '-') f = 1;
for (x = (c ^ 48); isdigit(c = CHARRECEI); x = (x << 1) + (x << 3) + (c ^ 48));
return f ? -x : x;
}
template<class T> inline void readin(T& x) {
x = 0; int f = 0; char c;
while (!isdigit(c = CHARRECEI)) if (c == '-') f = 1;
for (x = (c ^ 48); isdigit(c = CHARRECEI); x = (x << 1) + (x << 3) + (c ^ 48));
if (f) x = -x;
}
template<class T, class... Args> inline void readin(T& x, Args&... args) {
readin(x), readin(args...);
}
template<class T> inline void writln(T x, char c = '\n') {
if (x < 0) putchar('-'), x = -x;
static int __stk[55], __bit = 0;
do __stk[++__bit] = x % 10, x /= 10; while (x);
while (__bit) putchar(__stk[__bit--] ^ 48);
putchar(c);
}
} // namespace Elaina
using namespace Elaina;
const int maxn = 3e5;
const int logn = 19;
int r[maxn + 5], n;
vector<pii> tre[maxn + 5];
inline void input() {
readin(n);
rep (i, 1, n) readin(r[i]);
int u, v, w;
rep (i, 2, n) {
readin(u, v, w);
tre[u].push_back({ v, w });
tre[v].push_back({ u, w });
}
}
int ncnt;
vector<int> g[maxn * logn + maxn + 5];
namespace DS {
bool used[maxn + 5];
int siz[maxn + 5], mx[maxn + 5];
void findrt(int u, int par, int n, int& rt) {
siz[u] = 1, mx[u] = 0;
for (const auto& [v, w]: tre[u]) if (!used[v] && v != par) {
findrt(v, u, n, rt), siz[u] += siz[v];
chkmax(mx[u], siz[v]);
}
chkmax(mx[u], n - siz[u]);
if (mx[u] < mx[rt]) rt = u;
}
vector<pair<ll, int>> Dep, Radi;
/** recalculate @p siz[] at the same time */
void dfs(int u, int par, ll d) {
siz[u] = 1;
Dep.push_back({ d, u });
Radi.push_back({ r[u] - d, u });
for (const auto& [v, w]: tre[u]) if (!used[v] && v != par)
dfs(v, u, d + w), siz[u] += siz[v];
}
inline void link(int u, int v) { g[u].push_back(v); }
inline void calc(int u) {
Dep.clear(), Radi.clear();
Dep.push_back({ 0, u });
Radi.push_back({ r[u], u });
for (const auto& [v, w]: tre[u]) if (!used[v])
dfs(v, u, w);
sort(Dep.begin(), Dep.end());
sort(Radi.begin(), Radi.end());
int p = 0, cnt = static_cast<int>(Dep.size()), pre = -1;
for (const auto& [r, u]: Radi) {
// to avoid array overbound
assert(ncnt <= maxn * logn + maxn);
int fake = ++ncnt;
link(u, fake);
while (p < cnt && r >= Dep[p].fi)
link(fake, Dep[p++].se);
if (~pre) g[fake].push_back(pre);
pre = fake;
}
}
void launch(int, int);
void divide(int u) {
// printf("divide :> u == %d\n", u);
used[u] = true; calc(u);
for (const auto& [v, w]: tre[u]) if (!used[v])
launch(v, siz[v]);
}
void launch(int u, int n) {
if (n == 1) return ;
int rt = 0; mx[0] = n + 1;
findrt(u, 0, n, rt);
divide(rt);
}
} // namespace saya
int stk[maxn * logn + maxn + 5], ed;
bool inst[maxn * logn + maxn + 5];
int dfn[maxn * logn + maxn + 5], low[maxn * logn + maxn + 5], dfc;
int bel[maxn * logn + maxn + 5], bcnt;
void tarjan(int u) {
dfn[u] = low[u] = ++dfc;
inst[stk[++ed] = u] = true;
for (const int& v: g[u]) {
if (!dfn[v]) tarjan(v), chkmin(low[u], low[v]);
else if (inst[v]) chkmin(low[u], dfn[v]);
}
if (low[u] == dfn[u]) {
int x; ++bcnt;
do {
inst[x = stk[ed--]] = false;
bel[x] = bcnt;
} while (x ^ u);
}
}
int deg[maxn * logn + maxn + 5]; // size is only maxn requied
signed main() {
freopen("infect.in", "r", stdin);
freopen("infect.out", "w", stdout);
input();
ncnt = n;
DS::launch(1, n);
rep (i, 1, ncnt) if (!dfn[i]) tarjan(i);
rep (u, 1, ncnt) for (const int& v: g[u]) {
if (bel[u] != bel[v]) ++deg[bel[v]];
}
int ans = 0;
rep (i, 1, bcnt) if (!deg[i]) ++ans;
writln(ans);
return 0;
}
