\[\color{red}{\textsf{小游者,真神人也,左马桶,右永神,会执利笔破邪炁,何人当之?}} \\
\begin{array}{|}
\hline
\color{pink}{\text{A small swimmer is a God.}} \\
\color{pink}{\text{The left toilet and the right eternal God}} \\
\color{pink}{\text{can break the evil energy with a sharp pen.}} \\
\color{pink}{\text{Who can resist him? }} \\
\hline
\end{array} \\
\begin{array}{|}
\hline
\color{green}{\text{小遊者は、神であり、左便器、右永神であり}} \\
\color{green}{\text{鋭いペンを持って真実を突き刺している。誰が彼に抵抗できるだろうか? }} \\
\hline
\end{array} \\
\begin{array}{|}
\hline
\color{lightblue}{\text{Petit voyageur, est Dieu aussi, toilettes gauche, Dieu éternel droit,}} \\
\color{lightblue}{\text{peut tenir un stylo tranchant pour briser le mal, qui devrait le faire?}} \\
\hline
\end{array} \\
\begin{array}{|}
\hline
\color{purple}{\text{Der Direktor ist wirklich ein Gott}} \\
\color{purple}{\text{mit einer Toilette links und Yongshen rechts}} \\
\color{purple}{\text{der einen spitzen Stift hält}} \\
\color{purple}{\text{um die Wahrheit zu durchdringen.}} \\
\color{purple}{\text{Wer kann ihm widerstehen? }} \\
\hline
\end{array} \\
\begin{array}{|}
\hline
\color{cyan}{\text{Ein kleiner Schwimmer ist ein Gott.}} \\
\color{cyan}{\text{Die linke Toilette und der rechte ewige Gott können }} \\
\color{cyan}{\text{die böse Energie mit einem scharfen Stift brechen.}} \\
\color{cyan}{\text{Wer sollte es sein?}} \\
\hline
\end{array} \\
\color{red}{\textsf{对曰:“无人,狗欲当之,还请赐教!”}} \\
\newcommand\brak[1]{\left({#1}\right)}
\newcommand\Brak[1]{\left\{{#1}\right\}}
\newcommand\d[0]{\text{d}}
\newcommand\string[2]{\genfrac{\{}{\}}{0pt}{}{#1}{#2}}
\newcommand\down[2]{{#1}^{\underline{#2}}}
\newcommand\ddiv[2]{\left\lfloor\frac{#1}{#2}\right\rfloor}
\newcommand\udiv[2]{\left\lceil\frac{#1}{#2}\right\rceil}
\newcommand\lcm[0]{\operatorname{lcm}}
\newcommand\set[1]{\left\{{#1}\right\}}
\newcommand\ceil[1]{\left\lceil{#1}\right\rceil}
\newcommand\floor[1]{\left\lfloor{#1}\right\rfloor}
\newcommand\rhs[1]{\;\text{Rhs}\;#1}
\newcommand\lhs[1]{\;\text{Lhs}\;#1}
\newcommand\Vec[1]{\vec{\mathbf{#1}}}
\newcommand\rank[0]{\text{rank}}
\newcommand\group[1]{\left\langle\right\rangle}
\]
芝士速补!
半平面交の定义
一条直线将平面分为两个半平面,不妨假设一条直线 \(p_0p_1\) 的方向向量 \(\Vec v=p_1-p_0\) 的 左边 是该直线对应的半平面。
而一个点 \(p\) 在 \(p_0p_1\) 半平面上即 \(p_0-p_1-p_2\) 向左拐,也即 \(\Vec v\times \overrightarrow{p_2-p_1}>0\).
而半平面交就是很多个半平面的交集(点集、边集),显然,半平面交的结果会是一个凸区域。
求出半平面交
有几种不同的做法。
增量法
在线算法,每次加入一个半平面,就可以求出一个半平面交。由于平面无限,比较难处理,先放入一个很大的矩形使得整个平面变得有限,更方便处理。
然后每给出一条有向直线(半平面),就计算它与前面所形成的半平面交的点集,并判断前面的半平面的点集有哪些在直线右边,如果在右边有扔掉,转而在该位置放下被扔掉点的前后两条边与直线的交点,如果在该直线右边,则加入点集,否则不加入。
这种方法复杂度显然是 \(\mathcal O(n^2)\) 的,但是可以在算法结束后直接得到凸多边形的点集。
排序增量算法
先将所有直线按照极角排序,然后按照极角从小到大加入直线,维护两个集合:边集和点集。下面用图演示这个过程多图警告!
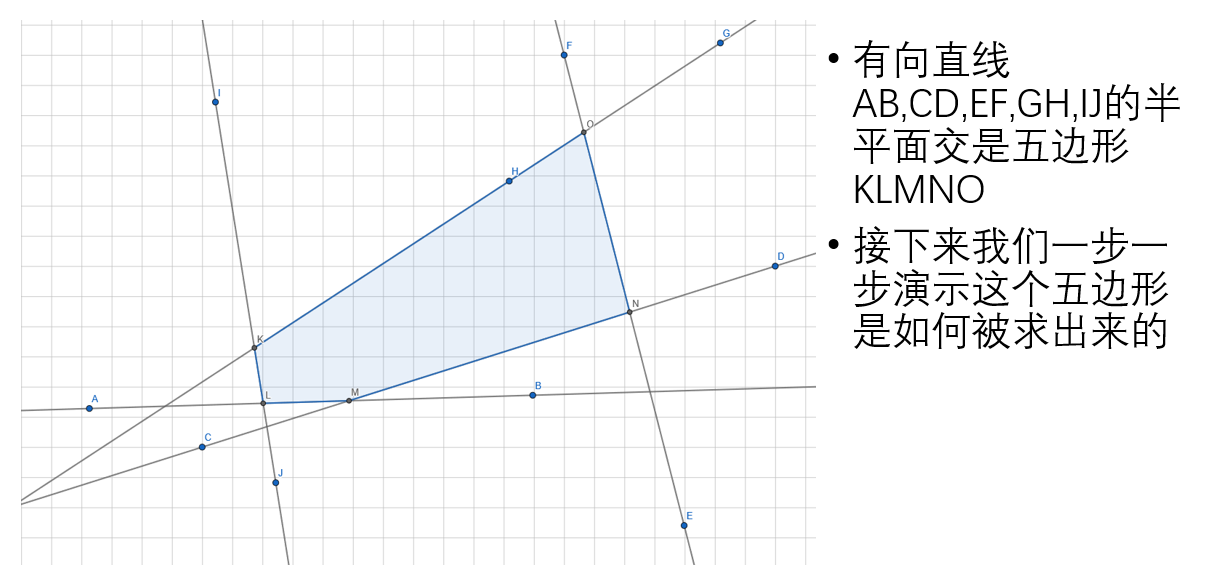
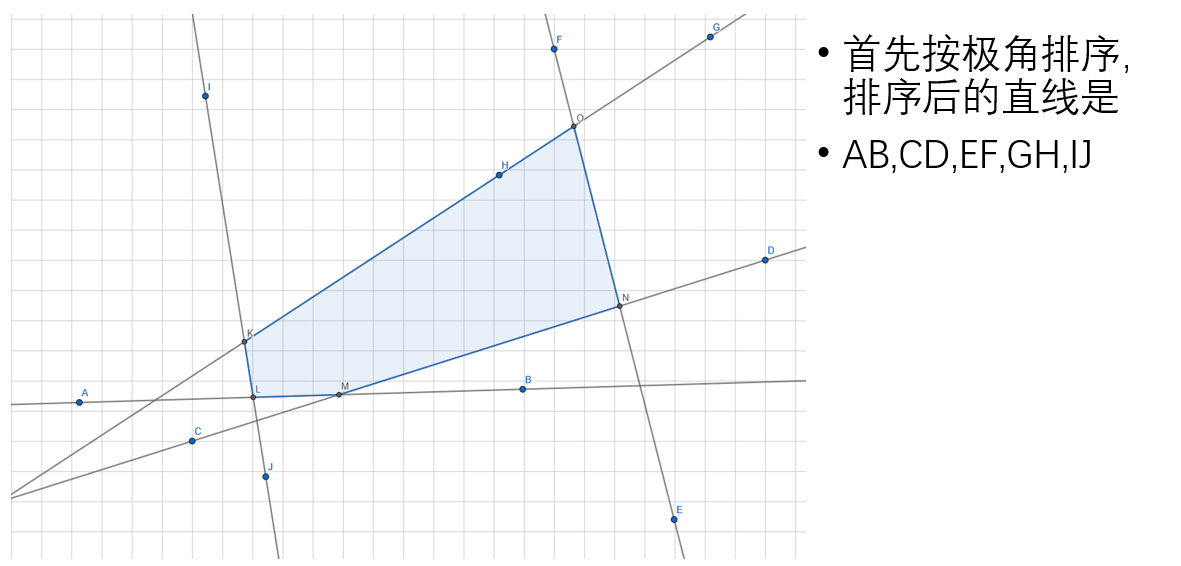
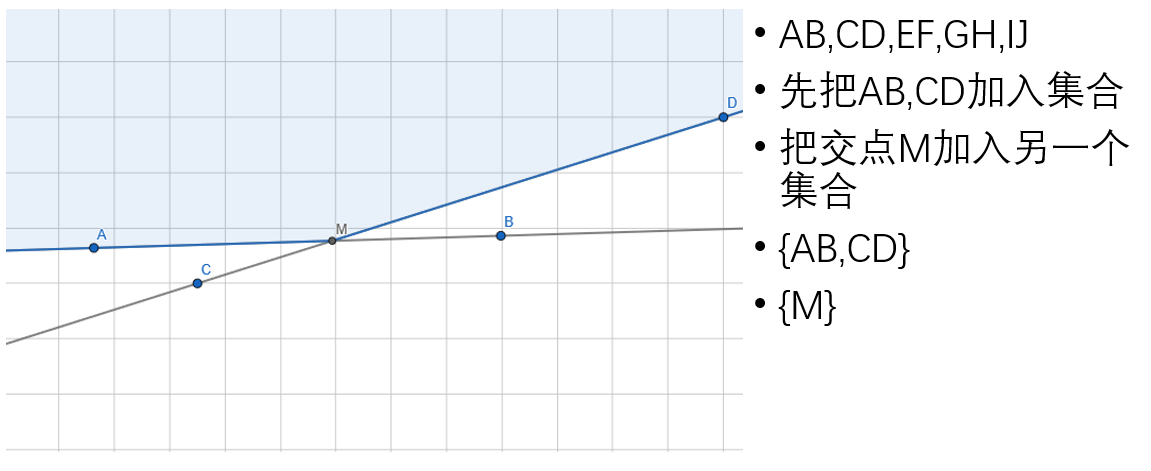
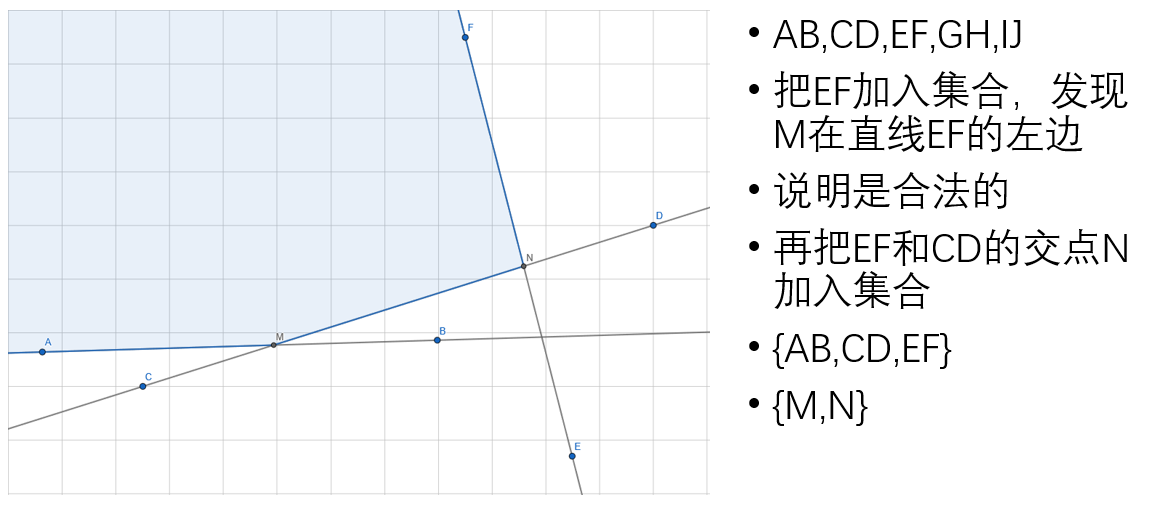
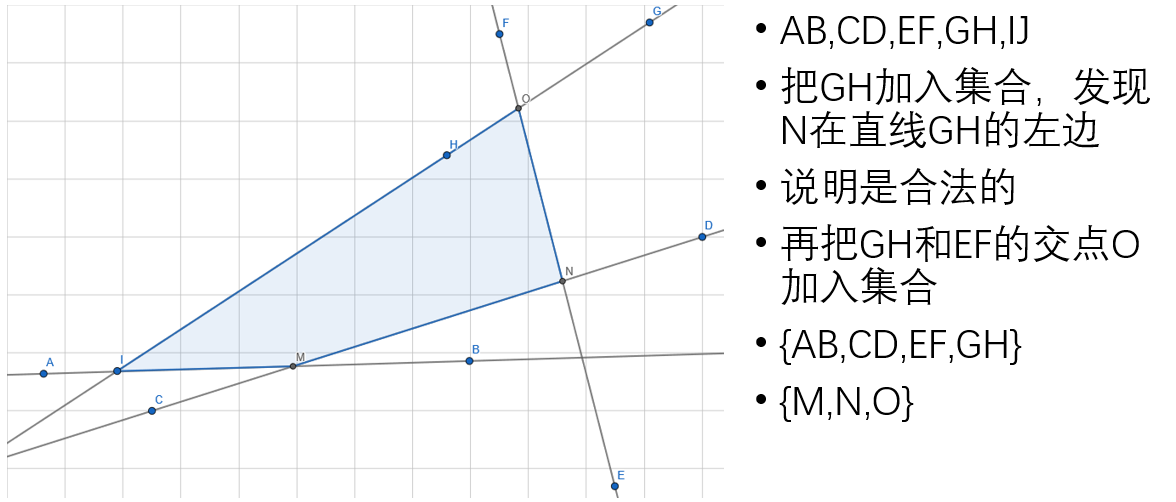
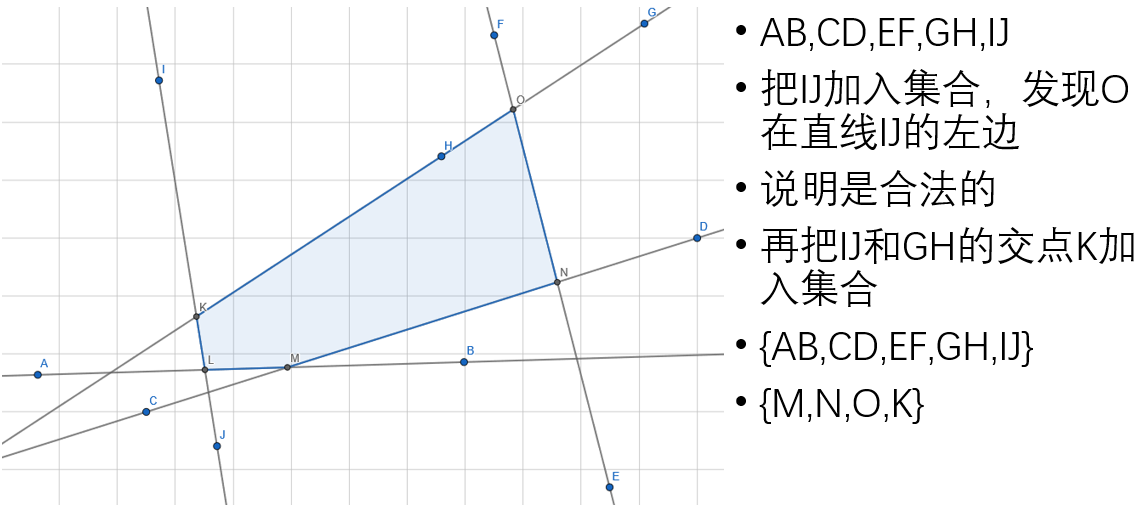
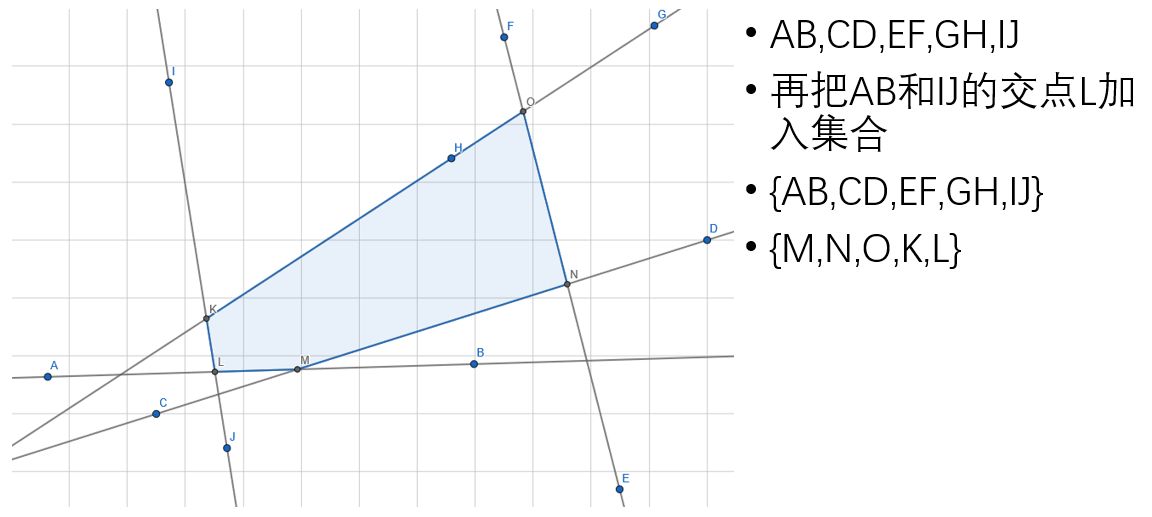
但是不是所有构建半平面交的时候都是这么理想,实际上有很多不合法情况,比如这种:
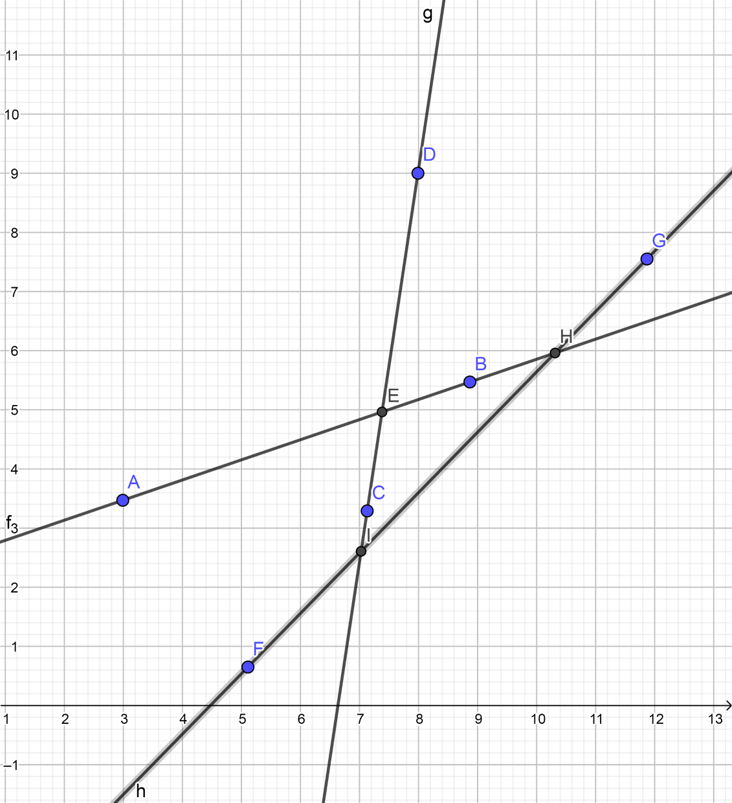
我们将会先加入 \(AB\),然后是 \(FG\),最后是 \(CD\),但是我们发现,在 \(AB,FG\) 后,加入 \(CD\) 时,发现 \(H\) 和 \(FG\) 都在 \(CD\) 的右边,说明 \(H\) 和 \(CD\) 实际上都不会在下凸壳上,从对应集合中删去他们就行。(注意描述直线时字母顺序实际上给蕴含了该有向直线的方向)
这个过程看上去和做凸包好像很想,那么我们能否用一个栈来构建?事实是,这个栈还得双向开口,如果有个这样的顺序:
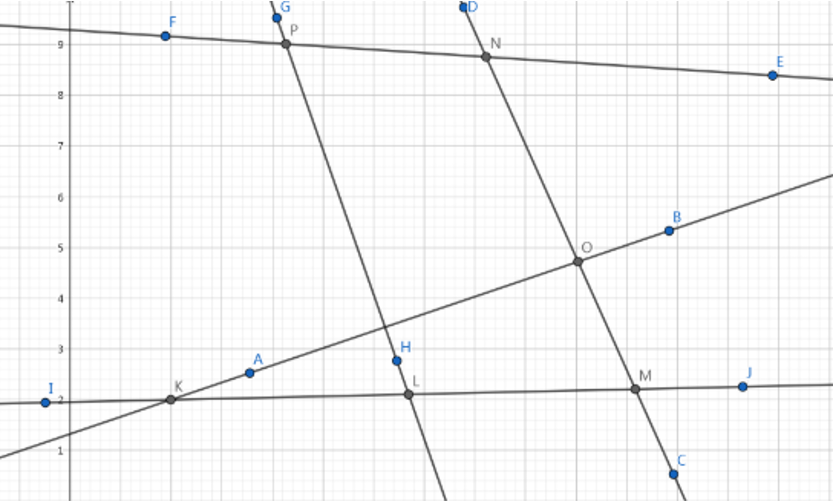
现有有向直线 \(IJ,AB,CD,EF,GH\),我们按照这个顺序加入直线,当加入到直线 \(GH\) 加入的时候,你会发现你想将 \(K\) 弹出去,但是 \(K\) 是点集中出现的第一个交点(直线 \(IJ,AB\) 的交点),因此栈需要双向开口。然后你会发现在处理完之后的栈会有两种情况:
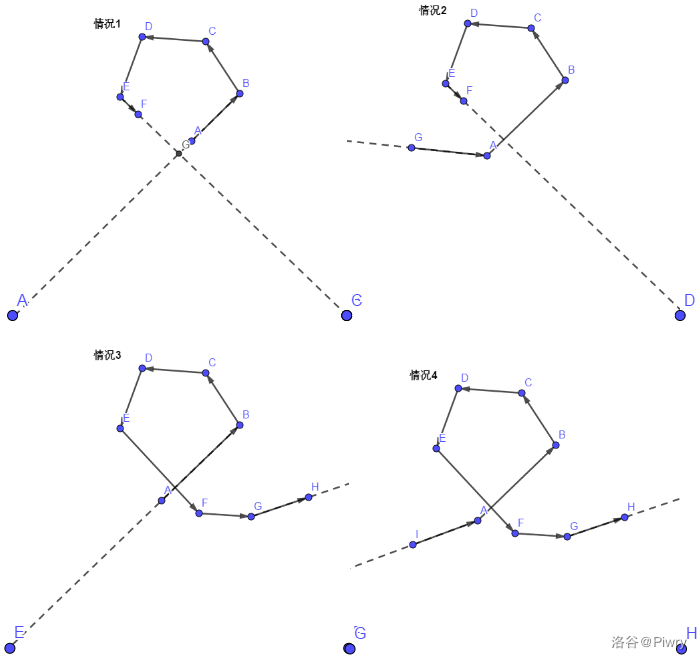
因为我们每次将双端队列两端不合法的情况去掉,因此最后只有可能出现情况 \(1,3\)(当然,情况 \(3\) 中的 \(A\) 点不在队列中),所以我们最后再用队首直线去判断一下队尾元素即可。
在实际寻找半平面交的时候,应当注意一些边界情况:
- 交的区域为 \(0\) 且封闭,即退化为了一个点或者一条线段;
- 交的区域无限的情况(不封闭);
- 相邻直线夹角大于 \(\pi\);
- 相邻直线夹角刚好为 \(\pi\),这个时候交为一条直线区域,它可能和其他直线交出一条射线;












 浙公网安备 33010602011771号
浙公网安备 33010602011771号