[学习笔记]第二次线代战争
曾经写过一篇关于线代的博客,但是感觉问题很大,一是排版,二是专业术语不严谨,三是有许多错误,四是不是特别形象,于是就没管那篇了,重新写一篇,可能有采纳原来那一篇的部分内容,但同时,有一些是我在看完 \(\textsf{3B1B}\) 之后的一些笔记,可能后面还有会更新,不过现在就这么多了。总而言之,这篇博客是为了能够更形象地解释线代而作,同时方便自己的复习。可以两篇结合一起看。
注意,本篇文章的重点在与矩阵相关的理解上,类似 “向量是什么”“矩阵乘法是怎么运算的” 将会比较省略。另外,除了一章比较特别,其他章节除特殊交代外,都在分析方阵。
壹、矩阵、矩乘的本质
矩阵,可以看做是多个列向量拼起来,即对于方阵 \(A\),它可以看成是
其中 \(\Vec{v_i}\in \Bbb R^n\),这就是一个 \(n\times n\) 的方阵。那么这一堆向量拼起来的这个矩阵有什么意义呢?我们不妨将每一个向量都看作是某一维的基底,也就是说,对于一个 \(n\) 维空间,它原本的基底拼起来的方阵是 \(I_n\),即 \(n\) 维意义下的单位阵,因为第 \(i\) 维的基底就是该维的长度为 \(1\) 且指向正方向的向量。那么,对于 \(I_n\),我们乘上一个 \(A\) 会发生什么?\(A\times I_n=A\),即在 \(A\) 的作用之后,\(I_n\) 变成了 \(A\). 这个过程可以形象地理解为基底的变换,而其他的地方,因为他们的坐标没有变,但是由于基底变了,所以它们也有对应的变化。
也就是说,左乘一个方阵,实际上就是一个线性变换的作用,或者在空间上对基底的变换。
举个例子,就用上面的 \(A=(\Vec {v_1}|\Vec{v_2}|\Vec{v_3}|\cdots|\Vec{v_n})\),我们考虑 \(\Vec w=(x_1,x_2,\cdots,x_n)\) 在经过 \(A\) 变换的结果:
\[A\Vec w=x_1\Vec {v_1}+x_2\Vec {v_2}+\cdots+x_n\Vec{v_n} \]让我们继续吧!
现在考虑另外的问题,两个矩阵乘起来会得到什么?举个例子,假设我们有 \(A,B\) 两个 \(n\) 阶方阵,那么 \(A\times B\) 对的结果是什么?这太抽象了,我们不妨举个例子:现在有一个 \(\Vec v\in \Bbb R^n\),结合前面所说,\(B\times \Vec v\) 将会得到 \(\Vec v\) 经过 \(B\) 变换之后的 \(n\) 阶向量,那么 \(A\times (B\times \Vec v)\) 就会得到 “\(\Vec v\) 先经过 \(B\) 变换再经过 \(A\) 变换” 的向量,根据矩阵的运算,\(A\times (B\times \Vec v)=(A\times B)\times \Vec v\),那么我们可以很形象地理解矩阵乘法了:不同变换叠加的结果。为了更好地说明这个东西,下面再举一个例子:
试计算
\[\begin{bmatrix} 0 & -2 & 2 \\ 5 & 1 & 5 \\ 1 & 4 & -1 \end{bmatrix} \begin{bmatrix} 0 & 1 & 2 \\ 3 & 4 & 5 \\ 6 & 7 & 8 \end{bmatrix} =\;? \]
当然你可以直接进行计算得到 \(3\times 3\) 的方阵,但是这里并不会说这种方法肯定不是我懒,我们介绍另一种方法。
我们已经知道了矩阵的乘法是变换的叠加,我们不妨将左边的矩阵看作 \(A\),右边的矩阵看作 \(B\),同时,设 \(B=(\Vec{v_1}|\Vec{v_2}|\Vec{v_3})\),当经过 \(B\) 变换之后,原来 \(I_3\) 的基底将会变成 \(\hat i=\Vec{v_1},\hat j=\Vec{v_2},\hat k=\Vec{v_3}\),再经过 \(A\) 变换,就是 \(\hat i,\hat j,\hat k\) 分别经过 \(A\) 变换之后再组成空间的基底,于是,上述矩乘得到的矩阵实际上就是:
即三个基底分别变换之后再拼起来得到组合的效果。这样,我们不难得到最后的答案:(建议自己先算一算再看答案)
我绝对是用手算的!!!
贰、矩阵的行列式
我们已经知道矩阵实际上是对基底的变换了,而这种变换既有对于空间的拉伸,又有压缩,当然也存在不拉伸也不压缩的情况,仅仅只是旋转、剪切之类的操作。不过,为了描述一个变换对于空间的放缩情况,我们引入行列式这个概念。形象地,行列式形容的是原来一个单位(原来的大小为 \(1\)),经过矩阵变换之后的大小。举个例子(假设他们都是满秩的),一阶方阵,就是一个长度为 \(1\) 的线段经过拉伸或压缩之后的长度;二阶方阵,就是一个面积为 \(1\) 的正方形经过变换之后的面积;三阶方阵,就是一个体积为 \(1\) 的小立方体,在基底经过变换之后它的体积。我们将其记为一个方阵的行列式,即 \(\det A\).
不过,上述说的并不完全正确 —— 显然,大家一定也见过行列式为负的情况,这种情况的出现,是源于该变换对于基底的空间位置关系进行了颠覆,举个例子,一维矩阵,\(\det([4])=4\) 而 \(\det([-3])=-3\),后者为负是因为它将 \(\hat i=[1]\) 变换为了 \(\hat i'=[-3]\),它原来指向 \(x\) 正方向,但是变换之后的 \(\hat i'\) 竟然指向了负方向!这对于原来的数轴来说,就好像是将该数轴 “翻了一翻”;二维矩阵,本来的二维空间,\(\hat j\) 应该在 \(\hat i\) 的左边(用叉积说明方向),但是,对于某些变换来说,经过该变换之后 \(\hat j\) 在 \(\hat i\) 右边,这也是一种空间位置关系的颠覆,就好像是将这个平面翻转了一下;三维空间也是类似,本来 \(\hat i,\hat j,\hat k\) 应该满足叉积的右手定则,但是变换之后,你只能用左手来做 “右手”定则,这也说明该变换行列式为负。
另外还有一些情况 —— 行列式为 \(0\),这显然不仅仅是一个变换了,因为,一个正常的变换,是不会将单位的大小变为 \(0\) 的,考虑什么时候一个单位的大小会变成 \(0\):三维空间中,一个立方体体积变成 \(0\),就相当于它变成了一个平面,一条线或一个点,也就是说,原本三维的概念,经过该变换之后变成了更低维度的东西。也就是说,虽然这个变换是三阶的,但是它的实质却只有二阶、一阶或零阶,可以形象地称其为维度的坍缩,这个时候我们称其为不满秩,这在下一章还会提到。
接下来,我们考虑说明一个东西:
两个变换叠加起来的放缩比率就相当于它们各自放缩比率之积。
如果真的想要求行列式,可以通过高斯消元法在 \(\mathcal O(n^3)\) 内求出,而不用按照定义在 \(\mathcal O(n!)\) 内求解它。
叁、矩阵的逆、列空间与核(零空间)
一般面对一个方程:
我们当然可以将其看做三个涉及 \(x,y,z\) 的方程,当然,我们也可以看做是矩阵与向量作用的结果:
为了看做是方阵和向量之积,我们不得不添上几个 \(0\). 而它实际上就是:
我们已知 \(A,\Vec v\),想要求 \(\Vec x\).
形象上来说,我们想要求的 \(\Vec x\) 经过 \(A\) 变换之后得到了 \(\Vec v\),反过来说,我们想要求一个 \(\Vec x\),让它经过 \(A\) 变换之后能够得到 \(\Vec v\).
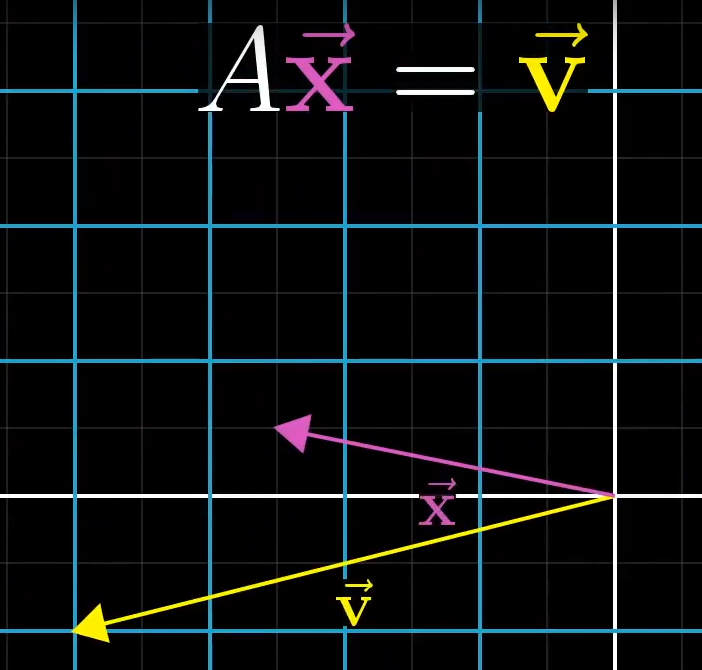
一个容易想到的思路是,我们找到一个 \(A^{-1}\),它是 \(A\) 的逆矩阵(形象的理解,逆变换?),经过这个逆矩阵的变换,我们就可以求得 \(\Vec x=A^{-1}\Vec v\). 显然,这个逆变换 \(A^{-1}\) 一定满足 \(A^{-1}A=I\). 这个思路简洁明了,一步到位!
如果想要求 \(A^{-1}\),可以通过高斯消元法将 \((A|I)\rightarrow (I|A^{-1})\),这里不赘述。
不过这个方法要有一个前提 —— 我们一定可以找到 \(A\) 的逆矩阵,不过,也不是所有的 \(A\) 都有对应的逆矩阵的,对于某些 \(\det=0\) 的矩阵,我们无法找到这样一个矩阵,为什么?由前面所说,当 \(\det A=0\) 也就是它不满秩的时候,它的本质并非是将空间变换成以另一组向量为基底的空间,而是将该空间坍缩为一个更低维度的东西,举个例子:
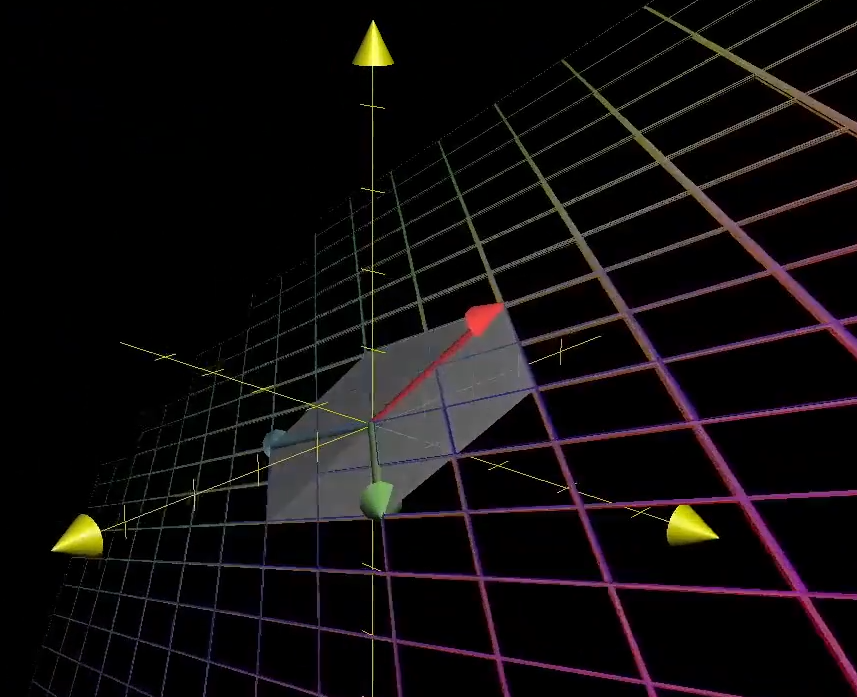
这个时候,三维的空间变成了二维的平面,由于逆变换实际上是将 \(\Vec v\) 变成我们想求的 \(\Vec x\),但是现在,显然,可能存在多个 \(\Vec x\) 都可以经过该变换得到 \(\Vec v\),做个类比:
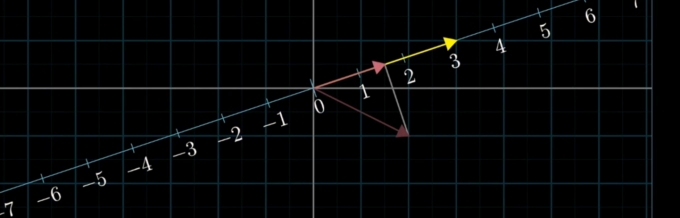
如果我们将向量沿一条直线作投影,显然会有多个向量在这条线上的投影都是一样的,而我们的变换只支持 “输入一个向量,输出一个向量”,它显然不可能做到 “解压缩”。不过,这也不意味着解一定不存在,下面这张截图很形象地说明了这个问题:
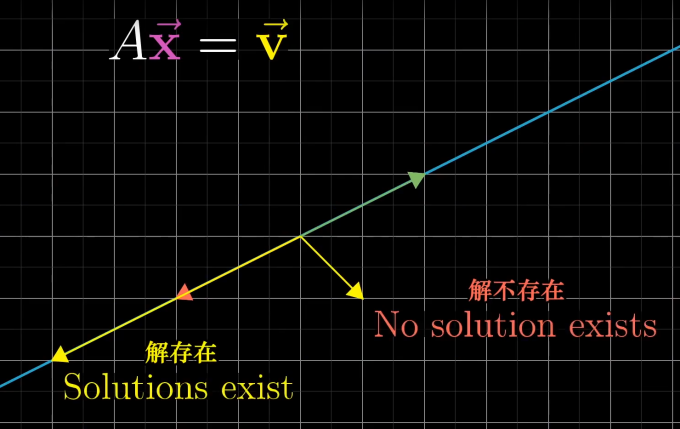
另外,同样 \(\det=0\),有些情况下解存在的条件更加苛刻,比如,在上图中,最后空间被压缩成了一个点,而非一条直线,这个时候存在解当且仅当 \(\Vec v=(0,0)\),而前者只要 \(\Vec v\) 在直线上即可。
那么我们如何区分这两种 \(\det=0\) 的情况?引入新的概念:秩(\(\rank\)),秩即形容了一个变换实质是几阶的,比如,上图中,将一个二维平面压缩成一维的直线,我们则说其秩为 \(1\). 秩其实代表着变换之后的空间维数,比如,一个二阶方阵,其秩最大为 \(2\),这意味着基向量仍然能够张成二维的平面,不过,对于三阶方阵来说,秩为 \(2\) 意为着原本的空间经过变换之后坍缩为一个二维平面,但是相比于秩为 \(1\),坍缩并非这么严重。
经过 \(A\) 变换之后的所有可能的输出向量组成的集合我们称其为该矩阵的 “列空间”,它其实就是方阵所有列向量所张成的空间,这样,更严谨地,矩阵的秩实际上就是该矩阵列空间的维数,当秩与列向量数量相同时,此时秩达到最大值,同时,我们称这种情况为 “满秩”。
对于一个满秩的矩阵 \(A\) 来说,唯一能够在变换之后还落在原点的,只有 \(\Vec 0\) 自身,而如果 \(A\) 不是满秩的,由于它将一个空间压缩到更低的维度,可能会有很多向量都落在原点,我们将这些向量构成的集合成为该矩阵的 “零空间” 或者 “核”,即 \(\ker(\mathscr A)=\set{\Vec x|\mathscr A\Vec x=\Vec 0}\).
肆、对于非方阵的特殊说明
非方阵其实很有意思,它可以将一个维度的一堆向量处理成为另外一个维度。直接说可能有点抽象,我们举个例子:
这就很有意思了,因为变换矩阵 \(A_{3\times 2}\) 将一堆二维向量变成了三维然后深藏功与名,这看上去是升维了,但是他们实际上还是拘泥于三维空间中由 \(\Vec {v_1}=(2,-1,-2)\) 与 \(\Vec {v_2}=(0,1,1)\) 张成的二维平面,所谓让你看到了高级的东西,但是却不给你,让你更绝望。
由上面这个例子,实际上我们已经可以总结出非方阵乘法各个参数的含义了:
- 对于变换矩阵:其行数为输出向量的维数,列数为接受向量的维数(原本空间的维数);
- 对于被变换的向量矩阵:其行数为其原本所处空间的维数,列数为被变换的向量的数量;
值得注意的是,组向量经过该变换之后已经不再处于原来的空间,因为空间的维数都不一样。我们另外举个例子,对于变换矩阵 \(A_{2\times 3}\) 来说,它接受原本维数为 \(3\) 的向量组,将他们映射为维数为 \(2\) 的向量组,或者将三维空间映射到二维空间;对于 \(A_{3\times 2}\) 来说,它接受 \(2\) 阶向量,将其映射到 \(3\) 阶向量,或者将二维空间映射到三维空间。
伍、点积与对偶性
点积,由于其运算大家都应该知道,这一点就不解释了。
不过,就其几何意义来说,\(\Vec v\cdot \Vec w\) 即将 \(\Vec v\) 作 \(\Vec w\) 上的投影,然后再乘以 \(\Vec w\) 的模长,这和 \(\Vec w\cdot\Vec v\) 的过程似乎完全不一样,但是为什么有 \(\Vec v\cdot\Vec w=\Vec w\cdot\Vec v\) ?这个神奇的交换律有它的特别之处,我们先从多维到一维的线性变换入手。
所谓线性变换,直观上将,如果是二维空间中你有一系列等距分布在某一条直线上的点,它们在应用变换之后,仍然保持等距分布在输出空间中,反之,如果这些点没有等距分布,那么该变换就不是线性变换。
举个例子,现在我们有个变换 \(\displaystyle \begin{bmatrix}1 & -2\end{bmatrix}\),容易发现它接受一系列二维向量,并将他们映射到一维空间(数轴)中,假设我们现在有个二维向量 \(\displaystyle \begin{bmatrix}4\\3\end{bmatrix}\),它在经过变换之后得到的结果是 \(\displaystyle \begin{bmatrix}1 & -2\end{bmatrix}\begin{bmatrix}4\\3\end{bmatrix}=4\cdot 1+3\cdot(-2)=-2\),而这个计算过程,感觉好像和计算两个向量的点积:\(\displaystyle \begin{bmatrix}1\\-2\end{bmatrix}\cdot\begin{bmatrix}4\\3\end{bmatrix}=4\cdot 1+3\cdot(-2)=-2\) 很像,并且我们发现,所谓的那个 “多维到一维” 的变换,就像是一个 “倾倒的向量”。我们不妨猜测,\(1\times 2\) 的矩阵与二维向量之间存在微妙的联系:将向量 “放倒”,从而得到一个与之相关的矩阵,而将矩阵直立,从而得到一个与之相关的向量。就长相上来看,简单地将矩阵直立或将向量放倒没有任何特殊的含义,但是我们可以从几何上理解。
在二维平面中,我们取一个数轴,考虑作任意向量在其上的投影,这显然是一个二维到一维的变换,即将一个二维的向量变成一维数轴上的一个数。
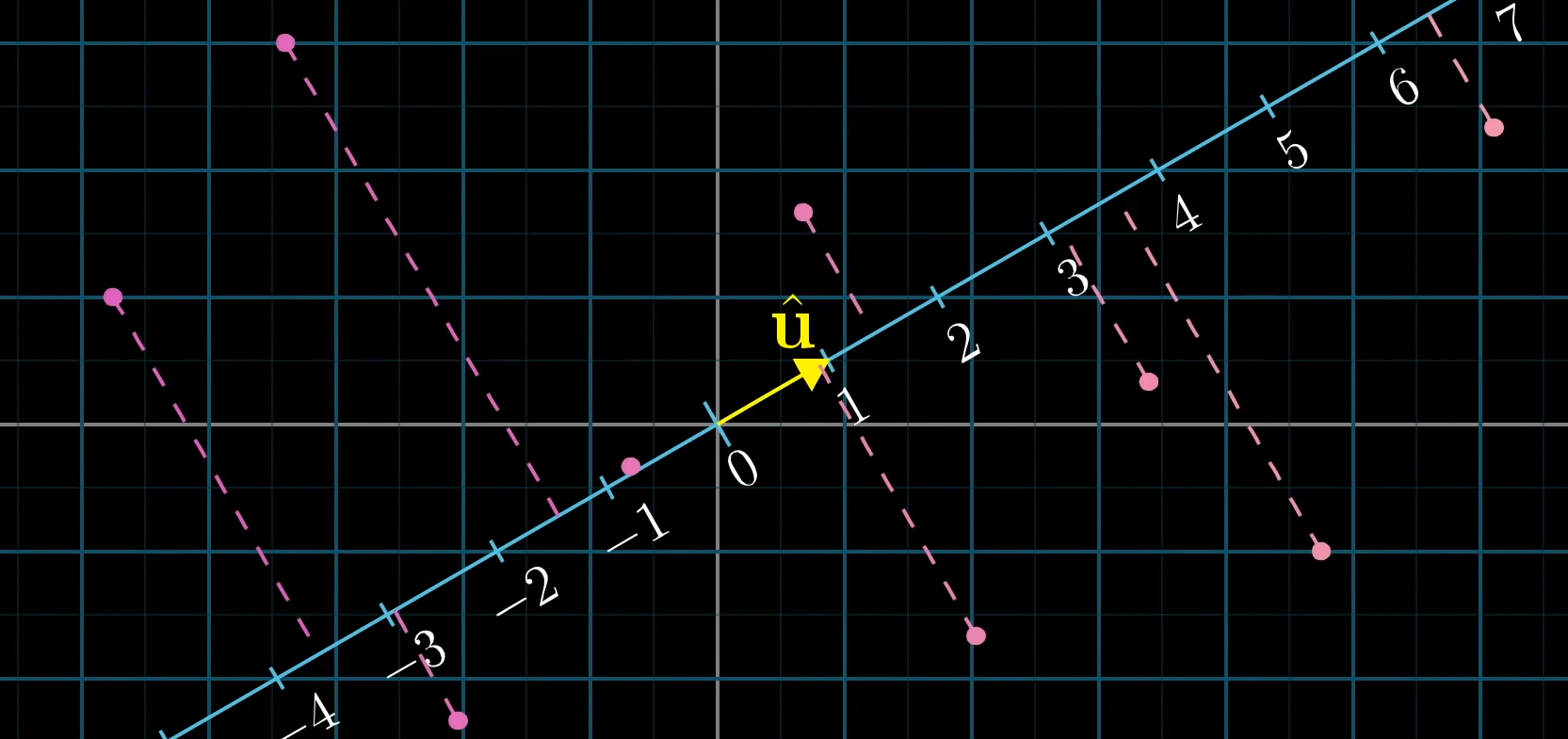
现在我们取其二维空间中一个特别的向量 \(\hat{\mathbf{u}}\),其指向数轴的正方向并且长度正好为 \(1\). 由前所说,所谓投影是一个二维向一维的变换,那么,我们的关注点应该放在,二维空间中,\(\hat i\) 和 \(\hat j\) 在经过该变换之后,去了哪里?
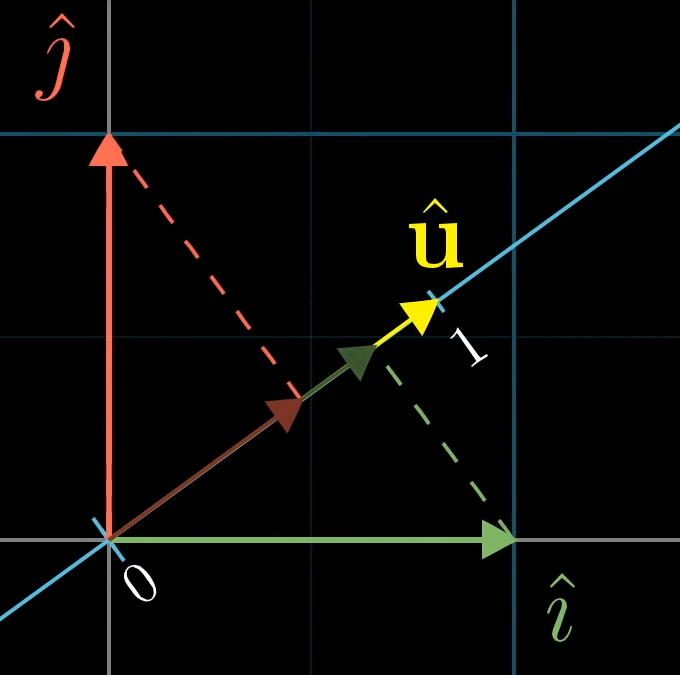
而要找到他们俩的去向,可以用对偶性很好地说明,我们先着眼于 \(\hat i\):
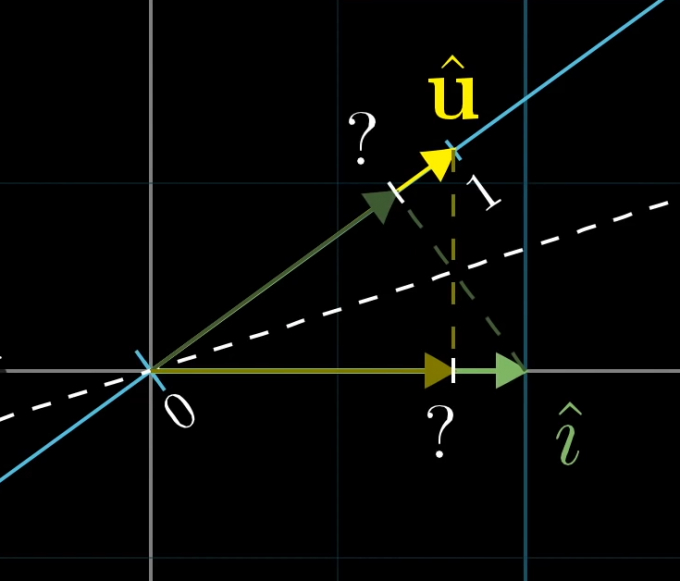
显然,由于 \(\hat{\mathbf{u}}\) 和 \(\hat i\) 的对偶性,\(\hat i\) 向数轴的投影在数值上等于 \(\hat{\mathbf{u}}\) 向 \(x\) 轴的投影,也就是 \(u_x\),同理,我们可以说明 \(\hat j\) 向数轴的投影就是 \(\hat{\mathbf{u}}\) 向 \(y\) 轴的投影,即 \(u_y\),也就是说,我们找到 \(\hat i,\hat j\) 的去向,那么可以构建出这个二维向一维的变换:\(\begin{bmatrix}u_x&u_y\end{bmatrix}\). 而我们观察该变换与空间任意向量 \(\displaystyle \Vec v=\begin{bmatrix}x\\y\end{bmatrix}\) 的作用:
因此,与单位向量的点乘可以解读为将向量投影到单位向量所在直线上的投影长度,而正负号则强调该向量与单位向量的方向上的关系。同样利用对偶性,我们可以很好地说明点乘具有交换律这一事实,此处就不再作说明。
另外,我们可以从中获得什么?无论什么时候,有一个多维空间向一维的变换,在该空间中,总会存在一个向量与该变换相关,而应用该变换和与该向量作点乘的效果一定会是一样的。而所谓对偶性,称其为 “偶”,正是因为他们之间天然存在联系而不可分割的关系,而对偶性的核心也就是两种数学事物之间存在自然而又出乎意料的对应关系。
而通过这一说明,我们同样也看到了向量的另一重身份 —— 它不仅仅只是一个箭头,有的时候,在某些时候,你也可以把它看成是一个线性变换的载体。
陆、叉积的特殊含义
由于上一章为了讲对偶性,点积讲得稍微详细了一点,但是叉积并没有什么必要的补充,因此,关于叉积的一般运算,以及 \(\Vec v\times \Vec w=\Vec p\) 和 \(\Vec p\) 的含义,并不准备说什么东西,只是有一个十分有意思的东西:
这个东西很有意思,可以分别从两边的含义入手,然后发现两边算的都是同一个东西的体积。因此,也可说\((\Vec v\times \Vec w)\) 向量与任意向量 \(\Vec p\) 的点积,即 \(\Vec v,\Vec w,\Vec p\) 三者构成的立体图形的体积,至于正负号,则反映了 \(\Vec v,\Vec w,\Vec p\) 是否满足叉积的右手定则.
柒、矩阵的转置
在线规那里想对偶问题的时候突然想到,网上关于其含义的阐释极简,十分不容易得找到一个写得特别好的回答,就引用到下面了。
先考虑特殊情况 —— 方阵的转置。但是这一特殊情况似乎并没有什么实际含义,如果我们将该矩阵作类似高斯消元的变换后,它会变成一个只有主对角线上有 \(1\) 的矩阵,将其转置后和本身是一样的,唯一不同的可能就只有系数。
特殊情况并不能交出一个对于矩阵转置的解答,这很不祥,但也只有硬着头皮想一想非方阵情况。
由于非方阵我们很熟悉其含义:不同维度之间的映射,接下来引用知乎大佬的回答了。
设 \(A\) 是一个 \(m\times n\) 的矩阵,则它表示了一个从 \(n\) 维空间到 \(m\) 维空间的映射;相应地,\(A^T\) 的大小是 \(n\times m\),它表示了一个从 \(m\) 维空间到 \(n\) 维空间的映射。另设 \(A\) 的秩为 \(r\)(\(A^T\) 的秩亦为 \(r\)),则上面的 \(n\) 维、\(m\) 维空间会被分割成四个子空间,如下图所示(图片来自 Gilbert Strang 的线性代数教材)。在左边的 \(n\) 维空间中任取一个向量 \(\Vec x\),则 \(A\Vec x\) 一定落在 \(A\) 的列空间中,即右边的 \(r\) 维子空间;在右边的 \(m\) 维空间中任取一个向量 \(\Vec y\),则 \(A^T\Vec y\) 一定落在 \(A\) 的行空间中,即左边的 \(r\) 维子空间。
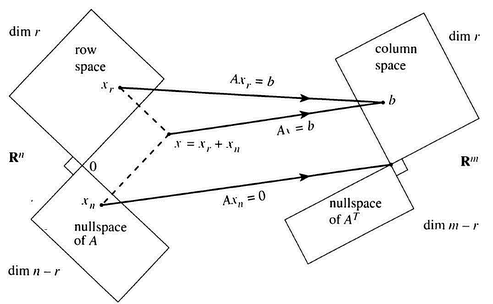
内积的角度
现在在左边的 \(n\) 维空间中取一个向量 \(\Vec x\),并在右边的 \(m\) 维空间中取一个向量 \(\Vec y\). 这两个向量属于不同的空间,我们想用线性映射的办法把它们映射到同一个空间中去。为此,我们可以用 \(A\) 把左边的 \(\Vec x\) 映射到右边的 \(A\Vec x\),也可以用 \(A^T\) 把右边的 \(\Vec y\) 映射到左边的 \(A^T\Vec y\). 我们对同一个空间中的两个向量求内积,可以发现,\(<\Vec x, A^T\Vec y> = \Vec x^TA^T\Vec y = (A\Vec x)^T\Vec y = <A\Vec x, \Vec y>\),也就是说,不管在哪一个空间中求内积,结果都是相等的。
于是我们可以这样描述转置的作用:「把左边的 \(\Vec x\) 映射到右边再与右边的 \(\Vec y\) 求内积」,可以与「把右边的 \(\Vec y\) 映射到左边再与左边的 \(\Vec x\) 求内积」相互替换,这两种操作中使用的映射,表示成矩阵时互为转置关系。
实际上,这两个映射互为伴随映射。
奇异值分解的角度
用内积来理解转置,似乎很抽象。那我再利用奇异值分解给出一种更具体的理解。
把 \(A\) 进行奇异值分解,得到 \(A = USV^T\),那么,若把 \(A^T\) 进行奇异值分解,就会得到 \(A^T = VSU^T\).
这几个矩阵的大小分别为:\(U:m\times r,\;S: r\times r,\;V: n\times r\).
我们看到,\(A\) 和 \(A^T\) 都可以分解成依次进行的三个映射。
其中,\(V,U\) 的各列分别是左、右两个 \(r\) 维子空间的单位正交基,所以三个映射中的第一步 \(V^T,U^T\) 的含义是把左、右两个空间中的向量投影到 \(r\) 维子空间中,再进行旋转操作(也可能包括翻转)。我们认为旋转的结果位于一个「中介 \(r\) 维空间」中,这个中介空间各个坐标轴上的单位向量对应着原空间的单位正交基。相应地,第三步 \(V,U\) 的含义就是把这个旋转逆过来,或者说把中介空间中的向量旋转回左、右两个 \(r\) 维子空间中去,但原先跟 \(r\) 维子空间垂直的分量就恢复不回来了。
而 \(S\) 是对角矩阵,所以第二步做的是伸缩。
这样 \(A\) 与 \(A^T\) 的关系就比较清晰了:
\(A\) 把左边 \(n\) 维空间中的 \(\Vec x\) 投影到左边的 \(r\) 维子空间中,旋转到中介 \(r\) 维空间里,沿各个坐标轴进行可能不同比例的伸缩,再旋转到右边的 \(r\) 维子空间中;
\(A^T\) 把右边 \(m\) 维空间中的 \(\Vec y\) 投影到右边的 \(r\) 维子空间中,旋转到中介 \(r\) 维空间里,沿各个坐标轴进行可能不同比例的伸缩,再旋转到左边的 \(r\) 维子空间中。
这两套操作中使用的旋转是互逆的,而伸缩的比例相等。
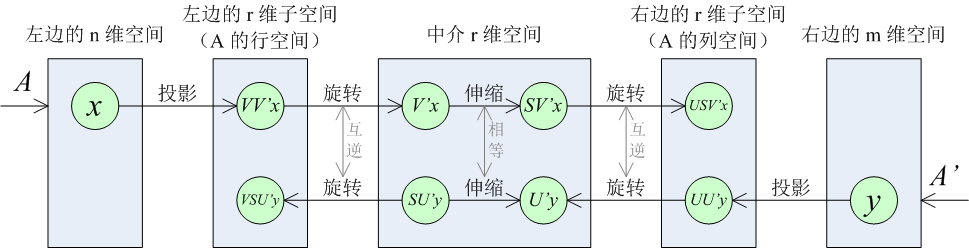
如果把中间的伸缩由「比例相等」改为「比例互为倒数」,那么两个矩阵就从转置关系变成了互逆关系。


