[噼昂!]operator(Pending)
壹、关于题目 ¶
仍然是没有时间去编......
贰、关于题解 ¶
竟然没有往括号树上面想......伊蕾娜大失败 😦 .
括号限制优先级,没有括号则可以直接 \(\rm DP\) 来做,而优先级,我们选择使用括号树对其进行翻译,然后,我们的 \(\rm DP\) 过程就变成了树上背包。
在 \(\rm DP\) 转移中有个关键处理的地方 —— 尾随符(\(\rm final\;note\))以及表达式(\(\rm Expression\))的划分。
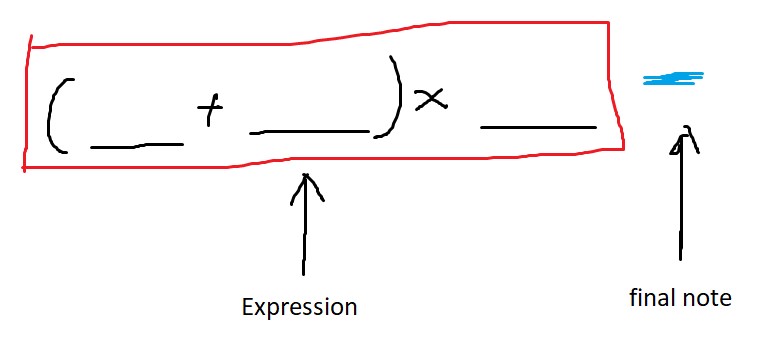
具体来说,我们应该维护两个东西:
- \(dp_{u,i}\),表示节点 \(u\) 一共使用了 \(i\) 个加号(不包含尾随符)所有方案的和;
- \(tmp\_dp_{i}\) 表示使用了 \(i\) 个加号(包含尾随符),每种方案 不包括最后一段连续乘法值 的和;
- \(cnt_i\),表示使用 \(i\) 个加号(不含尾随符)的方案数;
- \(tmp\_cnt_i\),表示使用 \(i\) 个加号(包含尾随符)的方案数;
- \(prod_i\),表示使用了 \(i\) 个加号,每种方案 最后一段连续乘法值 的和;
在 \(\rm DP\) 转移的时候,我们应当将前面的一堆儿子合并之后得到的 \(tmp\_dp,tmp\_cnt\) 与当前儿子的 \(dp,cnt\) 进行合并,并考察新的尾随符填 $+/\times $ 的不同贡献。
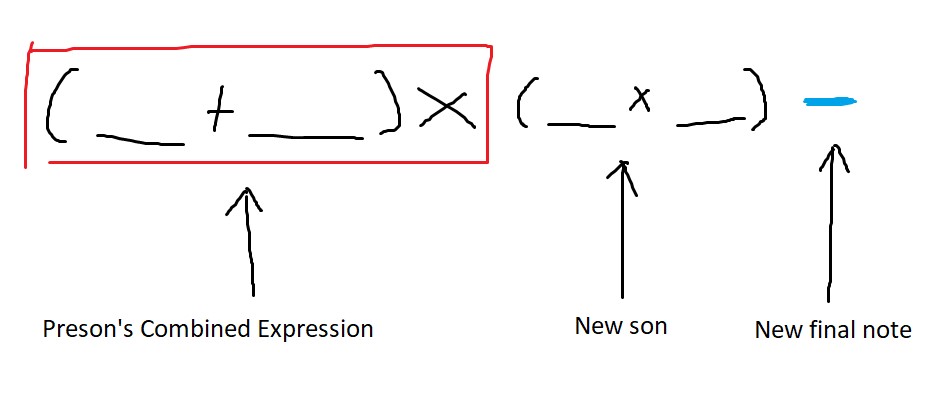
注意转移的时候不能直接改数组,还应该新开一个缓存数组储存,计算完毕之后拷贝进 \(tmp\) 数组与 \(prod\) 数组。
在处理最后一个儿子的时候,就不需要考虑新的尾随符了,所有的贡献可以直接计入 \(dp\) 与 \(cnt\) 数组。因为最后一个儿子象征着反括号,所有的这些都被合并为一个整体了。
看上去好像是 \(\mathcal O(n^3)\) 的,实际上是 \(\mathcal O(\max siz_u^2)(\sum siz = n)\),最劣情况为 \(\mathcal O(n^2)\).
叁、关于标程 ¶
#pragma GCC optimize("Ofast")
#include <bits/stdc++.h>
using namespace std;
# define USING_STDIN
// # define NDEBUG
// # define NCHECK
#include <cassert>
namespace Elaina {
#define rep(i, l, r) for(int i = (l), i##_end_ = (r); i <= i##_end_; ++i)
#define drep(i, l, r) for(int i = (l), i##_end_ = (r); i >= i##_end_; --i)
#define fi first
#define se second
#define mp(a, b) make_pair(a, b)
#define Endl putchar('\n')
#define whole(v) ((v).begin()), ((v).end())
#define bitcnt(s) (__builtin_popcount(s))
#ifdef NCHECK
# define iputs(Content) ((void)0)
# define iprintf(Content, argvs...) ((void)0)
#else
# define iputs(Content) fprintf(stderr, Content)
# define iprintf(Content, argvs...) fprintf(stderr, Content, argvs)
#endif
typedef unsigned int uint;
typedef long long ll;
typedef unsigned long long ull;
typedef pair <int, int> pii;
typedef pair <ll, ll> pll;
template <class T> inline T fab(T x) { return x < 0 ? -x : x; }
template <class T> inline void getmin(T& x, const T rhs) { x = min(x, rhs); }
template <class T> inline void getmax(T& x, const T rhs) { x = max(x, rhs); }
#ifndef USING_STDIN
inline char freaGET() {
# define BUFFERSIZE 1 << 17
static char BUF[BUFFERSIZE], *p1 = BUF, *p2 = BUF;
return p1 == p2 && (p2 = (p1 = BUF) + fread(BUF, 1, BUFFERSIZE, stdin), p1 == p2) ? EOF : *p1++;
# undef BUFFERSIZE
}
# define CHARGET freaGET()
#else
# define CHARGET getchar()
#endif
template <class T> inline T readret(T x) {
x=0; int f = 0; char c;
while((c = CHARGET) < '0' || '9' < c) if(c == '-') f = 1;
for(x = (c^48); '0' <= (c = CHARGET) && c <= '9'; x = (x << 1) + (x << 3) + (c ^ 48));
return f ? -x : x;
}
template <class T> inline void readin(T& x) { x = readret(T(1)); }
template <class T, class... Args> inline void readin(T& x, Args&... args) {
readin(x), readin(args...);
}
template <class T> inline void writc(T x, char s='\n') {
static int fwri_sta[55], fwri_ed = 0;
if(x < 0) putchar('-'), x = -x;
do fwri_sta[++fwri_ed] = x % 10, x /= 10; while(x);
while(putchar(fwri_sta[fwri_ed--] ^ 48), fwri_ed);
putchar(s);
}
} using namespace Elaina;
/**
* @param MOD used for modulo
* @param RT the primitive root of @p MOD
*/
template <int MOD, int RT> struct Mint {
int val;
static const int mod = MOD;
Mint(ll v = 0) { val = int(-mod < v && v < mod ? v : v % mod); if(val < 0) val += mod; }
inline friend bool operator == (const Mint& a, const Mint& b) { return a.val == b.val; }
inline friend bool operator != (const Mint& a, const Mint& b) { return !(a == b); }
inline friend bool operator < (const Mint& a, const Mint& b) { return a.val < b.val; }
inline friend bool operator > (const Mint& a, const Mint& b) { return a.val > b.val; }
inline friend bool operator <= (const Mint& a, const Mint& b) { return a.val <= b.val; }
inline friend bool operator >= (const Mint& a, const Mint& b) { return a.val >= b.val; }
inline Mint& operator += (const Mint& rhs) { return (*this) = Mint((*this).val + rhs.val); }
inline Mint& operator -= (const Mint& rhs) { return (*this) = Mint((*this).val - rhs.val); }
inline Mint& operator *= (const Mint& rhs) { return (*this) = Mint(1ll * (*this).val * rhs.val); }
inline Mint operator - () const { return Mint(-val); }
inline Mint& operator ++ () { return (*this) = (*this) + 1; }
inline Mint& operator -- () { return (*this) = (*this) - 1; }
inline friend Mint operator + (Mint a, const Mint& b) { return a += b; }
inline friend Mint operator - (Mint a, const Mint& b) { return a -= b; }
inline friend Mint operator * (Mint a, const Mint& b) { return a *= b; }
inline friend Mint qkpow(Mint a, ll n) {
assert(n >= 0); Mint ret = 1;
for(; n; n >>=1, a *= a) if(n & 1) ret *= a;
return ret;
}
inline friend Mint inverse(Mint a) { assert(a != 0); return qkpow(a, mod - 2); }
};
using mint = Mint <1000000007, 5>;
const int maxn = 1e5;
const int maxm = 2500;
int plus_require, n;
int val[maxn + 5];
char s[maxn + 5];
inline void input() {
readin(n, plus_require); scanf("%s", s + 1);
}
int nxt[maxn + 5];
namespace Build {
int stk[maxn + 5], ed;
inline void launch() {
rep(i, 1, n) {
if(s[i] == '(') stk[++ed] = i;
else if(s[i] == ')')
nxt[stk[ed--]] = i;
}
}
} // using namespace Build;
namespace Work {
mint dp[maxm + 5][maxm + 5]; // not include the final note (for there's no note)
mint cnt[maxm + 5][maxm + 5];
int siz[maxm + 5], ncnt;
vector <int> g[maxm + 5];
int solve(int l, int r) {
// the whole bracket
if(nxt[l] && nxt[l] == r) return solve(l + 1, r - 1);
/* <-- get the current node --> */
int u = 0, i = l;
/// the first element is a bracket
if(s[l] == '(') u = solve(l + 1, nxt[l] - 1), i = nxt[l] + 1;
else { /// otherwise a number
u = ++ncnt, dp[u][0] = 0, cnt[u][0] = 1, siz[u] = 1;
while(isdigit(s[i])) dp[u][0] = dp[u][0] * 10 + (s[i++] ^ 48);
}
/* <-- get the sons --> */
while(i <= r) {
while(s[i] == '-') ++i;
int v;
/// a bracket
if(s[i] == '(') v = solve(i + 1, nxt[i] - 1), i = nxt[i] + 1;
else { /// a number
v = ++ncnt, dp[v][0] = 0, cnt[v][0] = 1, siz[v] = 1;
while(isdigit(s[i])) dp[v][0] = dp[v][0] * 10 + (s[i++] ^ 48);
}
g[u].push_back(v);
}
if(g[u].empty()) return u; /// just a leaf
/** @brief maintain the current @p dp with the counter of %+ (include the final note) */
static mint tmp_cnt[maxm + 5] = {};
/** @brief maintain the current @p dp and also the note following (NOT include the final product) */
static mint tmp_dp[maxm + 5] = {};
/** @brief maintain the product of using @p i %+ (include the final note) */
static mint prod[maxm + 5] = {};
/// transfer the son's data into the tmp array & clear the @p dp and @p cnt
/// enumerate the number of %+
for(int j = 0; j < siz[u]; ++j) {
tmp_cnt[j] += cnt[u][j];
tmp_cnt[j + 1] += cnt[u][j];
/// no this statement, if the final note is %* then this is a prod
/// which isn't included in the definition of @p tmp_dp
// tmp_dp[i] += dp[u][i];
tmp_dp[j + 1] += dp[u][j];
prod[j] += dp[u][j];
prod[j + 1] += cnt[u][j];
dp[u][j] = cnt[u][j] = 0; /// clear for @p dp
}
static mint cache_tmpDp[maxm + 5] = {};
static mint cache_tmpCnt[maxm + 5] = {};
static mint cache_prod[maxm + 5] = {};
int lst_son = g[u].back();
for(int v : g[u]) {
/// for the first part include the final note, the number of %+ can reach the upper limit of @p siz[u]
for(int j = 0; j <= siz[u]; ++j) {
for(int k = 0; k < siz[v]; ++k) {
cache_tmpDp[j + k] += tmp_dp[j] * cnt[v][k];
cache_tmpDp[j + k + 1] += tmp_dp[j] * cnt[v][k] + prod[j] * dp[v][k];
cache_tmpCnt[j + k] += tmp_cnt[j] * cnt[v][k];
cache_tmpCnt[j + k + 1] += tmp_cnt[j] * cnt[v][k];
cache_prod[j + k] += prod[j] * dp[v][k];
cache_prod[j + k + 1] += tmp_cnt[j] * cnt[v][k];
if(v == lst_son) { /// the last son, need to update @p dp
dp[u][j + k] += tmp_dp[j] * cnt[v][k] + prod[j] * dp[v][k];
cnt[u][j + k] += tmp_cnt[j] * cnt[v][k];
}
}
}
/// transfer the cache into the variable
for(int j = 0; j <= siz[u] + siz[v]; ++j) {
tmp_dp[j] = cache_tmpDp[j];
tmp_cnt[j] = cache_tmpCnt[j];
prod[j] = cache_prod[j];
cache_tmpDp[j] = cache_tmpCnt[j] = cache_prod[j] = 0;
}
siz[u] += siz[v];
}
for(int j = 0; j <= siz[u]; ++j)
tmp_dp[j] = tmp_cnt[j] = prod[j] = 0;
g[u].clear(); /// a node may be used many times
return u;
}
inline void launch() {
int rt = solve(1, n);
writc(dp[rt][plus_require].val);
}
} // using namespace Work;
signed main() {
// freopen("operator.in", "r", stdin);
// freopen("operator.out", "w", stdout);
input();
Build::launch();
Work::launch();
return 0;
}
肆、关键 の 地方 ¶
括号等优先级问题,可以转到树上,每颗子树实际上就天然地限定了优先级。
另外,树上背包看上去十分暴力,但是用琴生分析一下,最劣情况只出现在其中某个 \(siz\) 最大,这个时候达到最劣的 \(\mathcal O(n^2)\).


