[HDU6829]Borrow
壹、关于题目 ¶
贰、关于题解 ¶
考虑设 \(f(i,j)\) 表示最大值和另外两个数相差为 \(i,j\) 时的轮数，显然如果合法的话，必定是 \(3\mid (i+j)\).
可以写出转移方程：
\[\begin{cases}
f(i,j)=\frac{1}{2}f(i-1,j-2)+\frac{1}{2}f(i-2,j-1)+1&i,j\ge 2 \\
f(i,0)=f(i-1,1)+2 \\
f(i,1)=f(i-2,0)+2 \\
f(0,0)=f(0,1)=0
\end{cases}
\]
后两者，事实上原转移存在环，并且环长度为 \(1\)，通过手算打开之后可以将环消掉。
显然，\(f(i,0)\) 与 \(f(i,1)\) 存在着递推关系，于是我们可以先 \(\mathcal O(n)\) 预处理出这个部分，然后再直接做 \(\rm DP\)，复杂度是 \(\mathcal O(n^2)\) 的。
不过，该转移有明显的组合意义，不妨将一个状态视作二维坐标系上的一个点，那么转移的图画出来就是这样的：
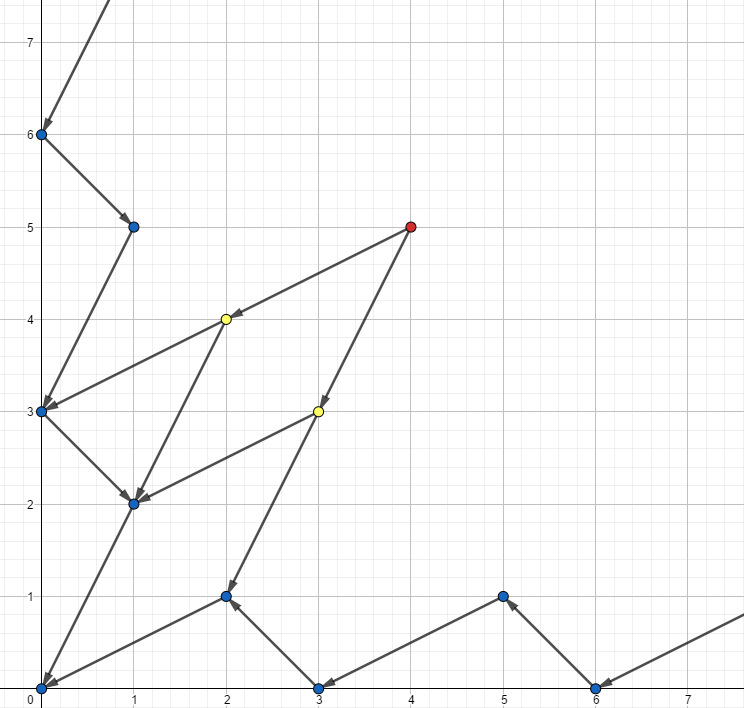
不难发现，似乎除了在坐标轴附近以外，其他点的转移都是每一次 “跳马步”，显然，从起点开始，走到 \(x\) 轴和走到 \(y\) 轴附近的情况是相似的，于是我们只讨论走到 \(x\) 轴附近的这种情况。
我们可以枚举最后跳到 \(x\) 轴附近的哪个位置：假设起点为 \(m,n\)，并假设最后我们跳到 \((p,0/1)\)，那么可以假设 \(dx=m-p,dy=n-0/1\)，假设最后要跳的总步数为 \(cnt\)，由于每一次 \(x,y\) 坐标总共减少 \(3\)，那么就有 \(cnt=\frac{dx+dy}{3}\)，设往 \(x\) 轴 \(-2\) 方向跳了 \(a\) 步，另一个方向跳了 \(b\) 步，那么
\[\begin{cases}
a+b=\frac{dx+dy}{3} \\
2a+b=dx \\
a+2b=dy
\end{cases}
\]
由于 \(dy\) 不固定，故并不是那么好处理 \(b\)，我们考虑解出 \(a=\frac{1}{3}(2dx-dy)\)，看似我们可以直接通过组合数学算出答案了，不过还有一个可能会算重的细节 —— \((p,0)\) 的上一步必须是 \((p+1,2)\)，如果不是这样，它可能会和从 \((p+2,1)\to (p,0)\) 的方案算重，我们减去这部分就可以了。
于是，我们可以得到：
- 点 \((p,1)\) 的贡献：\(\frac{1}{2^{cnt}}{cnt\choose a}(f(p,1)+cnt)\)；
- 点 \((p,0)\) 的贡献：\(\frac{1}{2^{cnt}}{cnt-1\choose a}(f(p,0)+cnt)\)；
枚举每个 \(p\) 即可。不过有几个细节：
- 不能直接枚举 \(p=0\)；
- 起点要分别从 \((x-y,x-z)\) 与 \((x-z,x-y)\) 出发，因为代码中只考虑跳到 \(y\) 轴的情况；
- 其实 \(a\) 的计算方法复杂了，直接 \(dx-cnt\) 就是 \(a\)，\(b\) 也是同理。
叁、参考代码 ¶
# include <bits/stdc++.h>
# include <bits/extc++.h>
using namespace std;
using namespace __gnu_pbds;
// # define USING_STDIN
// # define NDEBUG
# define NCHECK
# include <cassert>
namespace Elaina {
# define rep(i, l, r) for(int i=(l), i##_end_=(r); i<=i##_end_; ++i)
# define drep(i, l, r) for(int i=(l), i##_end_=(r); i>=i##_end_; --i)
# define fi first
# define se second
# define mp(a, b) make_pair(a, b)
# define Endl putchar('\n')
# define whole(v) ((v).begin()), ((v).end())
# ifdef NCHECK
# define iputs(Content) ((void)0)
# define iprintf(Content, argvs...) ((void)0)
# else
# define iputs(Content) fprintf(stderr, Content)
# define iprintf(Content, argvs...) fprintf(stderr, Content, argvs)
# endif
typedef unsigned int uint;
typedef long long ll;
typedef unsigned long long ull;
typedef pair <int, int> pii;
typedef pair <ll, ll> pll;
template <class T> inline T fab(T x) { return x < 0? -x: x; }
template <class T> inline void getmin(T& x, const T rhs) { x=min(x, rhs); }
template <class T> inline void getmax(T& x, const T rhs) { x=max(x, rhs); }
# ifndef USING_STDIN
inline char freaGET() {
# define BUFFERSIZE 5000
static char BUF[BUFFERSIZE], *p1=BUF, *p2=BUF;
return p1==p2 && (p2=(p1=BUF)+fread(BUF, 1, BUFFERSIZE, stdin), p1==p2)? EOF: *p1++;
# undef BUFFERSIZE
}
# define CHARGET freaGET()
# else
# define CHARGET getchar()
# endif
template <class T> inline T readret(T x) {
x=0; int f=0; char c;
while((c=CHARGET)<'0' || '9'<c) if(c=='-') f=1;
for(x=(c^48); '0'<=(c=CHARGET) && c<='9'; x=(x<<1)+(x<<3)+(c^48));
return f? -x: x;
}
template <class T> inline void readin(T& x) { x=readret(T(1)); }
template <class T, class... Args> inline void readin(T& x, Args&... args){
readin(x), readin(args...);
}
template <class T> inline void writc(T x, char s='\n') {
static int fwri_sta[55], fwri_ed=0;
if(x<0) putchar('-'), x=-x;
do fwri_sta[++fwri_ed]=x%10, x/=10; while(x);
while(putchar(fwri_sta[fwri_ed--]^48), fwri_ed);
putchar(s);
}
} using namespace Elaina;
/**
* @param MOD used for modulo
* @param RT the primitive root of @p MOD
*/
template<int MOD, int RT> struct Mint {
int val;
static const int mod=MOD;
Mint(ll v=0) { val=int(-mod<v && v<mod? v: v%mod); if(val<0) val+=mod; }
inline friend bool operator ==(const Mint& a, const Mint& b) { return a.val == b.val; }
inline friend bool operator !=(const Mint& a, const Mint& b) { return !(a==b); }
inline friend bool operator <(const Mint& a, const Mint& b) { return a.val<b.val; }
inline friend bool operator >(const Mint& a, const Mint& b) { return a.val>b.val; }
inline friend bool operator <=(const Mint& a, const Mint& b) { return a.val<=b.val; }
inline friend bool operator >=(const Mint& a, const Mint& b) { return a.val>=b.val; }
inline Mint& operator +=(const Mint& rhs) { return (*this)=Mint((*this).val+rhs.val); }
inline Mint& operator -=(const Mint& rhs) { return (*this)=Mint((*this).val-rhs.val); }
inline Mint& operator *=(const Mint& rhs) { return (*this)=Mint(1ll*(*this).val*rhs.val); }
inline Mint operator -() const { return Mint(-val); }
inline Mint& operator ++() { return (*this)=(*this)+1; }
inline Mint& operator --() { return (*this)=(*this)-1; }
inline friend Mint operator +(Mint a, const Mint& b) { return a+=b; }
inline friend Mint operator -(Mint a, const Mint& b) { return a-=b; }
inline friend Mint operator *(Mint a, const Mint& b) { return a*=b; }
inline friend Mint qkpow(Mint a, ll n) {
assert(n>=0); Mint ret=1;
for(; n; n>>=1, a*=a) if(n&1) ret*=a;
return ret;
}
inline friend Mint inverse(Mint a) { assert(a!=0); return qkpow(a, mod-2); }
};
using mint=Mint<998244353, 5>;
const int maxn=2e6;
mint fac[maxn+5], finv[maxn+5], pow2[maxn+5];
inline void prelude() {
int n=maxn;
fac[0]=finv[0]=pow2[0]=1;
rep(i, 1, n) fac[i]=fac[i-1]*i, pow2[i]=pow2[i-1]*2;
finv[n]=inverse(fac[n]);
drep(i, n-1, 1) finv[i]=finv[i+1]*(i+1);
}
inline mint C(int n, int m) {
return fac[n]*finv[m]*finv[n-m];
}
mint f[maxn+5][2];
inline void getf() {
for(int i=1; i<=maxn; ++i) {
if(i%3==0) f[i][0]=f[i-1][1]+2;
else if((i+1)%3==0) f[i][1]=f[i-2][0]+2;
}
}
inline mint solve(int m, int n) {
if(n<2) return f[m][n];
iprintf("m == %d, n == %d\n", m, n);
mint ret=0; int dx, dy, a, cnt;
for(int p=2; p<=m; ++p) {
dx=m-p;
for(int j=0; j<2; ++j) {
dy=n-j;
if((dx+dy)%3) continue;
cnt=(dx+dy)/3;
iprintf("When p == %d, j == %d, dx == %d, dy == %d, cnt == %d\n", p, j, dx, dy, cnt);
if(dx<cnt || dy<cnt) continue;
a=dx-cnt;
iprintf("dx == %d, dy == %d, cnt == %d, a == %d\n", dx, dy, cnt, a);
ret=ret+inverse(pow2[cnt])*C(cnt-(j^1), a)*(f[p][j]+cnt);
}
}
return ret;
}
signed main() {
prelude(); getf();
rep(_, 1, readret(1)) {
static vector<int>v(3);
rep(i, 0, 2) readin(v[i]);
if((v[0]+v[1]+v[2])%3) { puts("-1"); continue; }
sort(whole(v));
writc((solve(v[2]-v[0], v[2]-v[1])+solve(v[2]-v[1], v[2]-v[0])).val);
}
return 0;
}
肆、关键 の 地方 ¶
- 感觉转移有环时不妨手消几组，看看能不能把环打开；
- 比较简单的 \(\rm DP\) 方程可以考察一下组合意义；
