[专题讨论]线段树上的最大值
\(\rm update\;on\;2021/8/24\)
经过反复斟酌,我决定还是新开一篇博客记录这种方法。
壹、问题描述 ¶
单点询问历史最值:传送门 to UOJ .
区间询问历史最值:传送门 to Luogu .
这种方法是解决一系列区间取 \(\max\),区间询问最值,以及区间询问历史最值的问题的通法?
贰、题解 ¶
我们先不考虑历史最大值,想一想普通情况应该怎么做?首先,分析 \(3\) 操作,这是一个很特殊的操作。
对于每个 \(a_i\) ,将 \(a_i\) 修改为 \(\max(a_i-t,0)\).
从一般性的操作上似乎难以理解,但是我们可以从函数角度理解,它其实就是将函数 \(f(x)=\max(x-t,0)\) 作用在 \(a_i\) 上,我们试图寻找一般性规律,不妨对 \(f(x)\) 引入一些参数,使其变得一般化:
这个函数有什么性质呢?在机器的深度学习领域有大用处 我们试图画出一些图像,不难发现其就是一条拥有一个折点的折线。但是这似乎并没有什么特殊之处,我们继续挖掘该函数的性质。
尝试两个函数 \(f(x)=\max(x+a,b),g(x)=\max(x+c,d)\),然后再定义 \(h(x)=\max(f(x),g(x))\),它就是这个样子的:
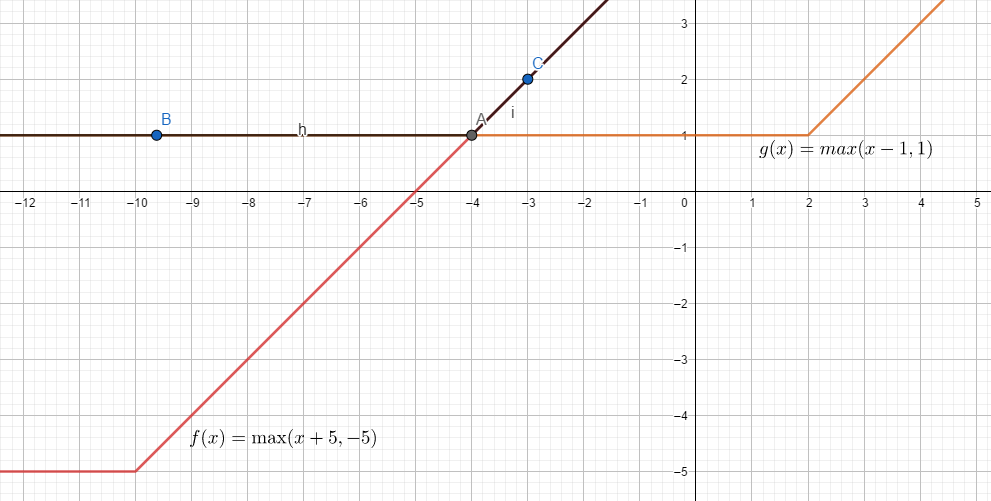
接下来,我们考察函数的复合,即形如 \(f(g(x))\),我们将其展开
最后的形式和我们最开始的形式很像,即得到的新函数 \(h(x)=x+(a+c)+\max(a+d,b)\),即,这种函数的复合还是这样的函数。函数的复合,启示这样定义的函数可以处理区间修改,并且我们发现,所有的修改都能写成这种形式:
定义二元组 \((a,b)\) 表示将函数 \(f(x)=\max(x+a,b)\) 作用在 \(a_i\) 上,那么:
- 区间加 \(v\),即 \((v,-\infty)\);
- 区间赋值 \(v\),即 \((-\infty,v)\);
- 区间减 \(v\)(与 \(0\) 取 \(\max\) ),即 \((-v,0)\);
- 询问,直接将所有覆盖该点的函数复合之后,将最初的 \(a_i\) 代入即可;
接下来考虑如何处理区间最大值,接下来引用 PPT 中的内容:
区间加就是在对应节点上打标记。在非历史值问题中,我们只关注该节点“当下”的标记是什么,所以我们会直接将标记合并起来。但在历史值问题中,我们不仅要考虑该节点现在的标记合并结果,还要考虑历史上推来的(按时间为序的)每个标记的依次作用。
为了便于理解,我们不合并标记,假设每个节点上有一个队列(按照时间先进先出),放着所有曾经推过来的标记。
下推标记时,将该节点上所有的标记推到两个儿子处,并清空队列。
对于每个节点,维护 \(x,m\) 分别表示 : 区间最值, 区间历史最值。
每次有一个区间加 \(t\) 标记推来时,令 \(x\leftarrow x+t\) 然后 \(m\leftarrow \max(m,x)\),注意,是先将 \(x\) 更新后再更新 \(m\).
我们寻找一种方法概括一个队列的标记对当前节点的影响。
先思考对一个点打若干次标记的情形。设推来的加法标记分别为 \(t[1:k]\),其前缀和为 \(S[1:k]\).
则打上第 \(i\) 个标记之后,\(x\) 的值为 \(x+S[i]\). 所以,\(m\) 的值为 \(\max_{i=1}^k\{x+S[i]\}=x+\max_{i=1}^k \{S[i]\}\).
于是,只需记录 \(\max_{i=1}^k \{S[i]\}\) 就能得知该标记队列对节点的影响。
合并加法标记的方法时简单求和,所以前 \(i\) 个标记合并后恰好等于 \(S[i]\),那么 \(\max_{i=1}^k \{S[i]\}\) 可以表述为标记的历史最大值 \(mt\).
接下来考虑两个队列如何合并,设为 \(t_1[1:k_1],t_2[1:k_2]\),合并后的结果为 \(t_3[1:k_1+k_2]\),前缀和为 \(s_3\)
\[\max_{i=1}^{k_1+k_2}\{s_3\}=t_3.mt=\max(\max_{i=1}^{k_1}\{s_1\},s_1[k_1]+\max_{i=1}^{k_2} \{s_2\})=\max(t_1.mt,t_1.t+t_2.mt) \]也就是在 \(t_1\) 的最大值基础上,再比较 \(t_1\) 整体与 \(t_2\) 的最大值。
具体地,设 \(t\) 为合并后的加法标记,\(mt\) 为加法标记的历史最大值。\(x\) 为区间最值,\(m\) 为区间历史最值,每次从 \(u\) 下推到 \(v\) 时:
\(v.m=max(v.m,v.x+u.mt)\);
\(v.mt=max(v.mt,u.mt+v.t)\);
\(v.x+=u.t\);
\(v.t+=u.t\);
\(u.t=u.mt=0\);
该 PPT 说明的是区间加法以及区间询问历史最值的情形,我们可以从其中类比这道题。
对于每个节点维护 \((a,b)\),历史叠加 \((p,q)\),区间最大值,区间历史最大值。
当修改 \((x,y)\) 来时,当前最大值 \(mx\) 将会成为 \((x,y)(mx)\),而历史最大值再和当前更新后的最大值比大小即可。
如何维护 \((a,b)\) 以及 \((p,q)\) ?对于 \((p,q)\),由我们上面那一套,其实就是 \((p,q)\) 与 \((x,y)\cdot(a,b)\) 的叠加,而 \((a,b)\) 就变成了 \((x,y)\cdot(a,b)\)。下传也是同样的思路。
解决区间历史最值,我们也可以同样解决单点最值。复杂度竟然只有 \(\mathcal O(n\log n)\).
叁、参考代码 ¶
单点查询历史最值
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <vector>
#include <cstring>
using namespace std;
// #define NDEBUG
#include <cassert>
namespace Elaina{
#define rep(i, l, r) for(int i=(l), i##_end_=(r); i<=i##_end_; ++i)
#define drep(i, l, r) for(int i=(l), i##_end_=(r); i>=i##_end_; --i)
#define fi first
#define se second
#define mp(a, b) make_pair(a, b)
#define Endl putchar('\n')
#define mmset(a, b) memset(a, b, sizeof a)
#define mmcpy(a, b) memcpy(a, b, sizeof a)
// #define int long long
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int, int> pii;
typedef pair<ll, ll> pll;
template<class T>inline T fab(T x){ return x<0? -x: x; }
template<class T>inline void getmin(T& x, const T rhs){ x=min(x, rhs); }
template<class T>inline void getmax(T& x, const T rhs){ x=max(x, rhs); }
template<class T>inline T readin(T x){
x=0; int f=0; char c;
while((c=getchar())<'0' || '9'<c) if(c=='-') f=1;
for(x=(c^48); '0'<=(c=getchar()) && c<='9'; x=(x<<1)+(x<<3)+(c^48));
return f? -x: x;
}
template<class T>inline void writc(T x, char s='\n'){
static int fwri_sta[1005], fwri_ed=0;
if(x<0) putchar('-'), x=-x;
do fwri_sta[++fwri_ed]=x%10, x/=10; while(x);
while(putchar(fwri_sta[fwri_ed--]^48), fwri_ed);
putchar(s);
}
}
using namespace Elaina;
const int maxn=5e5;
const ll inf=1ll<<50;
ll x[maxn+5];
int n, m;
namespace saya{
struct Func{
ll a, b;
inline Func operator +(const Func& rhs) const{
return Func{max(a, rhs.a), max(b, rhs.b)};
}
inline Func operator ^(const Func& rhs) const{
return Func{max(a+rhs.a, -inf), max(a+rhs.b, b)};
}
inline ll operator ()(const ll& x) const{ return max(x+a, b); }
};
Func tag[maxn<<2|2], histag[maxn<<2|2];
#define ls (i<<1)
#define rs (i<<1|1)
#define mid ((l+r)>>1)
#define fa (i>>1)
#define _lhs ls, l, mid
#define _rhs rs, mid+1, r
#define _this i, l, r
inline void update(int i){
histag[i]=histag[i]+(histag[fa]^tag[i]);
tag[i]=tag[fa]^tag[i];
}
inline void pushdown(int i){
update(ls), update(rs), tag[i]=histag[i]=Func{0, -inf};
}
void build(int i, int l, int r){
tag[i]=histag[i]=Func{0, -inf};
if(l==r) return;
build(_lhs), build(_rhs);
}
void modify(int L, int R, Func f, int i, int l, int r){
if(L<=l && r<=R){
histag[i]=histag[i]+(f^tag[i]);
tag[i]=f^tag[i];
return;
}
pushdown(i);
if(L<=mid) modify(L, R, f, _lhs);
if(mid<R) modify(L, R, f, _rhs);
}
ll query(int p, int type, int i, int l, int r){
if(l==r) return type? histag[i](x[p]): tag[i](x[p]);
pushdown(i);
if(p<=mid) return query(p, type, _lhs);
else return query(p, type, _rhs);
}
#undef ls
#undef rs
#undef mid
#undef fa
#undef _lhs
#undef _rhs
#undef _this
}
signed main(){
n=readin(1), m=readin(1);
rep(i, 1, n) x[i]=readin(1);
saya::build(1, 1, n);
int op, l, r, x, y;
while(m--){
op=readin(1);
if(op==1){
l=readin(1), r=readin(1), x=readin(1);
saya::modify(l, r, {x, -inf}, 1, 1, n);
}
else if(op==2){
l=readin(1), r=readin(1), x=readin(1);
saya::modify(l, r, {-x, 0}, 1, 1, n);
}
else if(op==3){
l=readin(1), r=readin(1), x=readin(1);
saya::modify(l, r, {-inf, x}, 1, 1, n);
}
else{
y=readin(1);
writc(saya::query(y, op-4, 1, 1, n));
}
}
return 0;
}
区间查询历史最值
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <vector>
#include <cstring>
using namespace std;
// #define NDEBUG
#include <cassert>
namespace Elaina{
#define rep(i, l, r) for(int i=(l), i##_end_=(r); i<=i##_end_; ++i)
#define drep(i, l, r) for(int i=(l), i##_end_=(r); i>=i##_end_; --i)
#define fi first
#define se second
#define mp(a, b) make_pair(a, b)
#define Endl putchar('\n')
#define mmset(a, b) memset(a, b, sizeof a)
#define mmcpy(a, b) memcpy(a, b, sizeof a)
// #define int long long
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int, int> pii;
typedef pair<ll, ll> pll;
template<class T>inline T fab(T x){ return x<0? -x: x; }
template<class T>inline void getmin(T& x, const T rhs){ x=min(x, rhs); }
template<class T>inline void getmax(T& x, const T rhs){ x=max(x, rhs); }
template<class T>inline T readin(T x){
x=0; int f=0; char c;
while((c=getchar())<'0' || '9'<c) if(c=='-') f=1;
for(x=(c^48); '0'<=(c=getchar()) && c<='9'; x=(x<<1)+(x<<3)+(c^48));
return f? -x: x;
}
template<class T>inline void writc(T x, char s='\n'){
static int fwri_sta[1005], fwri_ed=0;
if(x<0) putchar('-'), x=-x;
do fwri_sta[++fwri_ed]=x%10, x/=10; while(x);
while(putchar(fwri_sta[fwri_ed--]^48), fwri_ed);
putchar(s);
}
}
using namespace Elaina;
const int maxn=1e5;
const ll inf=1ll<<50;
ll x[maxn+5];
int n, m;
namespace saya{
ll mx[maxn<<2|2], hismx[maxn<<2|2];
struct Func{
ll a, b;
// overlay
inline Func operator +(const Func& rhs) const{
return Func{max(a, rhs.a), max(b, rhs.b)};
}
// composite, this(rhs(x))
inline Func operator ^(const Func& rhs) const{
// to compare the first key with -inf is because (-inf) + (-inf) = (-inf)
// in other word, we want to ensure that the variable don't overflow int range
return Func{max(a+rhs.a, -inf), max(a+rhs.b, b)};
}
inline ll operator ()(const ll& x) const{ return max(x+a, b); }
};
Func tag[maxn<<2|2], histag[maxn<<2|2];
#define ls (i<<1)
#define rs (i<<1|1)
#define mid ((l+r)>>1)
#define fa (i>>1)
#define _lhs ls, l, mid
#define _rhs rs, mid+1, r
#define _this i, l, r
// use father to update son
inline void update(int i){
histag[i]=histag[i]+(histag[fa]^tag[i]);
tag[i]=tag[fa]^tag[i];
hismx[i]=max(hismx[i], histag[fa](mx[i]));
mx[i]=tag[fa](mx[i]);
}
inline void pushdown(int i){
update(ls), update(rs), tag[i]=histag[i]=Func{0, -inf};
}
inline void pushup(int i){
mx[i]=max(mx[ls], mx[rs]), hismx[i]=max(hismx[ls], hismx[rs]);
}
void build(int i, int l, int r){
tag[i]=histag[i]=Func{0, -inf};
if(l==r) return mx[i]=hismx[i]=x[l], void();
build(_lhs), build(_rhs), pushup(i);
}
void modify(int L, int R, Func f, int i, int l, int r){
if(L<=l && r<=R){
mx[i]=f(mx[i]);
hismx[i]=max(hismx[i], mx[i]);
histag[i]=histag[i]+(f^tag[i]);
tag[i]=f^tag[i];
return;
}
pushdown(i);
if(L<=mid) modify(L, R, f, _lhs);
if(mid<R) modify(L, R, f, _rhs);
pushup(i);
return;
}
ll query(int L, int R, int type, int i, int l, int r){
if(L<=l && r<=R) return type? hismx[i]: mx[i];
ll ret=-inf;
pushdown(i);
if(L<=mid) ret=query(L, R, type, _lhs);
if(mid<R) ret=max(ret, query(L, R, type, _rhs));
return ret;
}
void check(int i, int l, int r){
printf("node %d, [%d, %d], mx == %lld, hismx == %d\n", i, l, r, mx[i], hismx[i]);
if(l==r) return;
pushdown(i);
check(_lhs), check(_rhs);
}
#undef ls
#undef rs
#undef mid
#undef fa
#undef _lhs
#undef _rhs
#undef _this
}
signed main(){
n=readin(1);
rep(i, 1, n) x[i]=readin(1ll);
saya::build(1, 1, n);
m=readin(1);
char op[5]; int x, y, z;
while(m--){
scanf("%s", op);
x=readin(1), y=readin(1);
if(op[0]=='Q') writc(saya::query(x, y, 0, 1, 1, n));
else if(op[0]=='A') writc(saya::query(x, y, 1, 1, 1, n));
else{
z=readin(1);
if(op[0]=='P') saya::modify(x, y, {z, -inf}, 1, 1, n);
else saya::modify(x, y, {-inf, z}, 1, 1, n);
}
}
return 0;
}


