[JLOI2015]骗我呢
壹、题目描述 ¶
贰、题解 ¶
◆ Observation
- 注意到每个严格上升子序列的长度都是 \(m\);
- 注意到序列的每个元素取值都在 \([0,m]\) 之间;
于是我们可以得到一个结论:每个严格上升子序列中,一定有且仅有一个数没有出现。
◆ 分离约束条件
似乎还是很难处理,发现关键在于,限制 \(x_{i,j}<x_{i-1,j+1}\) 将每一行都连接在一起了,我们可以先考虑在每一行中的情况。
我们称一个点 \((i,j)\) 为断点当其满足 \(x_{i,j}+1<x_{i,j+1}\),那么每一行一定最多只有一个断点,并且任意一个上升子序列也最多只会有一个断点,此时,我们再考虑 \(x_{i,j}\) 对于两行断点的限制。
若 \(i-1\) 行的断点为 \(j+1\),那么,显然地,第 \(i\) 行的断点出现的合法位置在 \([j,m]\),因为我们要保证,任意上升子序列最多一个断点,于是,我们可以设计 \(\rm DP\) 了。
设 \(f(i,j)\) 表示当第 \(i\) 行断点为 \(j\) 时的方案数,那么我们不难得到转移:
特殊情况,\(f(i,0)=f(i-1,0)+f(i-1,1)\),且 \(f(0,j)=f(0,j-1),f(0,0)=1\).
最后答案是什么呢?是 \(f(n, m)\) 吗?并不是,该状态表示的是第 \(n\) 行的断点在 \(m\) 时的方案数,最后的答案应为 \(\sum_{j=1}^nf(n,j)\),我们不妨多增加一行,最后,\(f(n+1,m)\) 就是答案了。
但是直接这样做显然是 \(\mathcal O(nm)\) 的,还不够。
◆ 将 DP 转化
不妨将转移的图画出来:
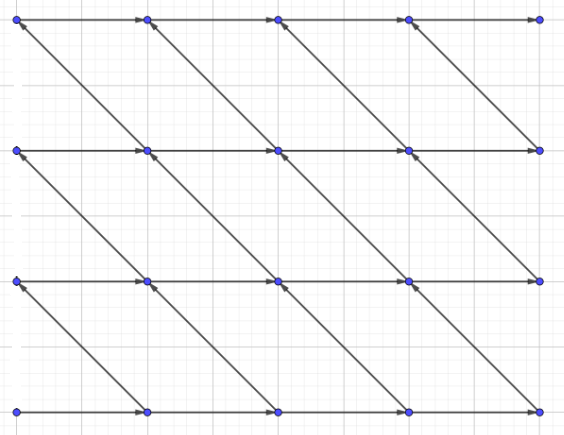
赶脚好像有点像走格子啊,我们把这个图拉一下,让它好看一点:
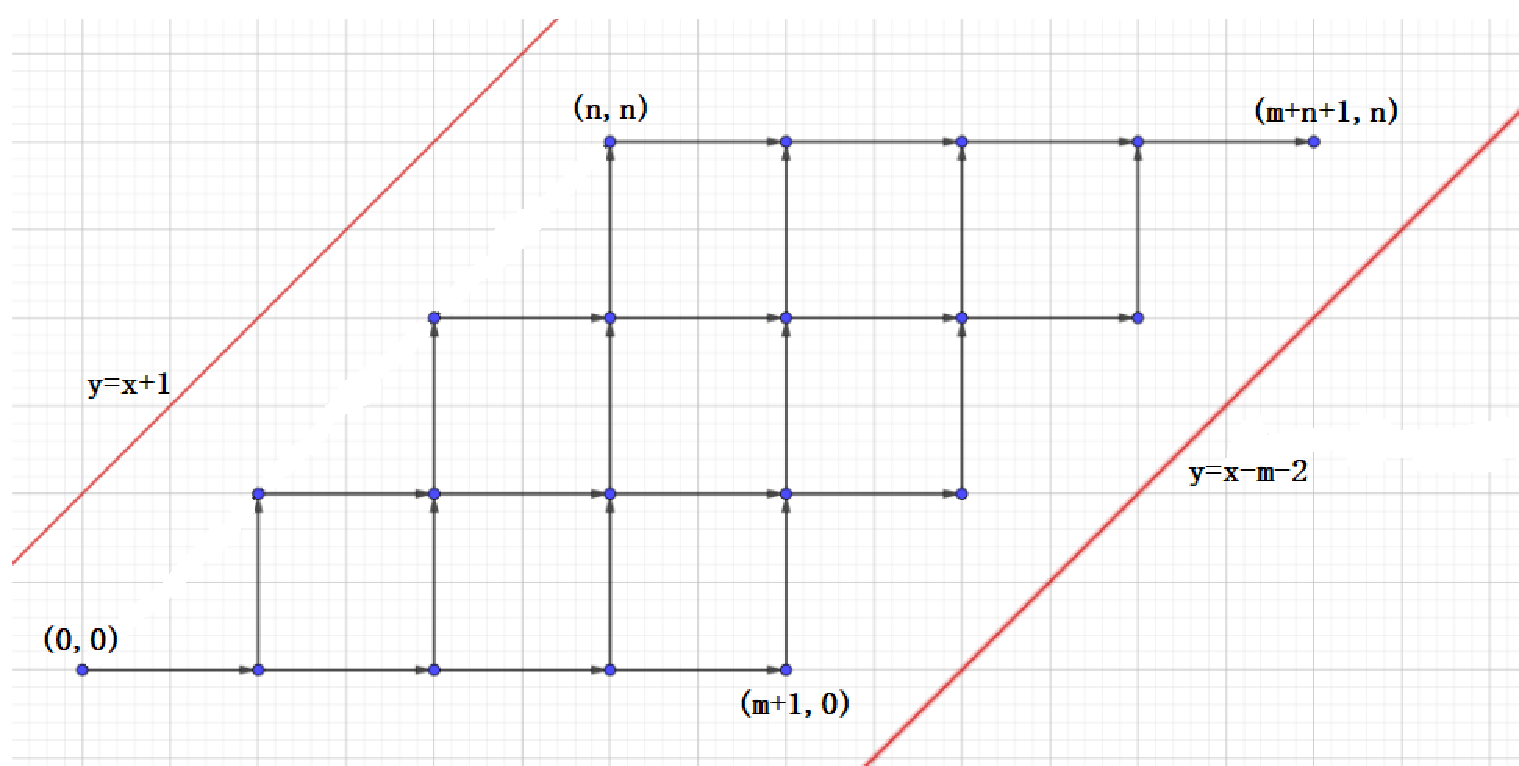
最后方案数,事实上就是从 \((0,0)\) 走到 \((m+n+1,n)\) 而不经过 \(l_1:y=x+1\) 以及 \(l_2:y=x-m-2\) 的方案数。
使用容斥,从总方案数中减去不合法的,总方案即 \(n+m+1\choose n\),但是不合法的呢?经过 \(1\) 的和经过 \(2\) 的,但是这样,\(12\) 和 \(21\) 就会被重复算,所以还要减去 \(12,21\) 的方案,但是 \(121,212\) 又会被全部减掉,所以还要加上 \(121,212\) 的方案,然后......
所以不难得到容斥过程,\(+1,+2,-12,-21,+121,+212,-1212,-2121,\cdots\).
至于如何算方案,就是将终点沿 \(l_1,l_2\) 不断翻折即可。
叁、参考代码 ¶
#include<cstdio>
#include<algorithm>
#include<vector>
#include<cstring>
#include<set>
using namespace std;
#define NDEBUG
#include<cassert>
namespace Elaina{
#define rep(i, l, r) for(int i=(l), i##_end_=(r); i<=i##_end_; ++i)
#define drep(i, l, r) for(int i=(l), i##_end_=(r); i>=i##_end_; --i)
#define fi first
#define se second
#define mp(a, b) make_pair(a, b)
#define Endl putchar('\n')
#define mmset(a, b) memset(a, b, sizeof a)
// #define int long long
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int, int> pii;
typedef pair<ll, ll> pll;
template<class T>inline T fab(T x){ return x<0? -x: x; }
template<class T>inline void getmin(T& x, const T rhs){ x=min(x, rhs); }
template<class T>inline void getmax(T& x, const T rhs){ x=max(x, rhs); }
template<class T>inline T readin(T x){
x=0; int f=0; char c;
while((c=getchar())<'0' || '9'<c) if(c=='-') f=1;
for(x=(c^48); '0'<=(c=getchar()) && c<='9'; x=(x<<1)+(x<<3)+(c^48));
return f? -x: x;
}
template<class T>inline void writc(T x, char s='\n'){
static int fwri_sta[1005], fwri_ed=0;
if(x<0) putchar('-'), x=-x;
do fwri_sta[++fwri_ed]=x%10, x/=10; while(x);
while(putchar(fwri_sta[fwri_ed--]^48), fwri_ed);
putchar(s);
}
}
using namespace Elaina;
const int mod=1e9+7;
const int maxn=3e6;
inline int qkpow(int a, int n){
int ret=1;
for(; n>0; n>>=1, a=1ll*a*a%mod)
if(n&1) ret=1ll*ret*a%mod;
return ret;
}
int fac[maxn+5], finv[maxn+5];
inline void prelude(){
fac[0]=finv[0]=1;
for(int i=1; i<=maxn; ++i)
fac[i]=1ll*fac[i-1]*i%mod;
finv[maxn]=qkpow(fac[maxn], mod-2);
for(int i=maxn-1; i>=1; --i)
finv[i]=1ll*finv[i+1]*(i+1)%mod;
}
inline int C(int n, int m){
if(n<m) return 0;
return 1ll*fac[n]*finv[m]%mod*finv[n-m]%mod;
}
int n, m;
inline int calc(int x, int y){
if(x<0 || y<0) return 0;
return C(x+y, x);
}
inline void flip1(int& x, int& y){
swap(x, y); --x, ++y;
}
inline void flip2(int& x, int& y){
swap(x, y); x+=(m+2), y-=(m+2);
}
signed main(){
prelude();
n=readin(1), m=readin(1);
int ans=calc(n+m+1, n);
int x=n+m+1, y=n;
while(x>=0 && y>=0){
flip1(x, y); ans=(0ll+ans+mod-calc(x, y))%mod;
flip2(x, y); ans=(0ll+ans+mod+calc(x, y))%mod;
}
x=n+m+1, y=n;
while(x>=0 && y>=0){
flip2(x, y); ans=(0ll+ans+mod-calc(x, y))%mod;
flip1(x, y); ans=(0ll+ans+mod+calc(x, y))%mod;
}
writc(ans);
return 0;
}

