[CF1450D]Rating Compression
壹、题目描述 ¶
贰、题解 ¶

如出一辙.
猜了一发 “答案除 \(k=1\) 时具有单调性” 然后就过了,不过是暴力的 \(\mathcal O(n\log n)\),二分答案 + \(\rm st\) 表优化最小值。
但是为什么使用 \(\rm st\) 表呢?因为俩 \(\log\) 被卡了 😦 .
但是为什么答案具有单调性呢?\(\sf closestool\) 给出了祂的证明:
假设当前区间长度为 \(k\) 并且合法,那么有这样一张图:
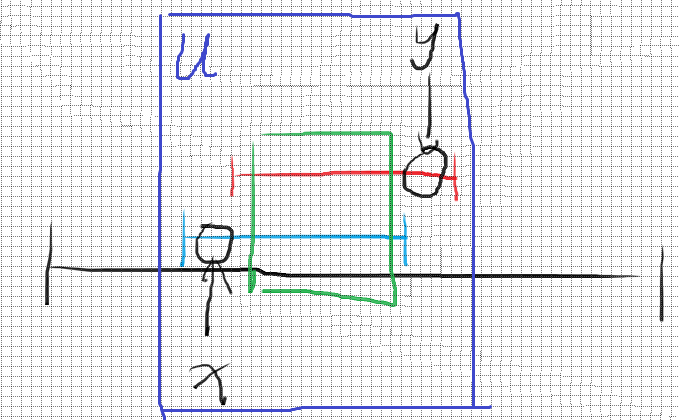
红蓝为两相邻区间,假设两个区间的最小值为 \(b_i,b_{i+1}\),由于他们的最小值是不同的,所以对于红蓝构成的整个大区间 \(U\),它的最小值不会出现在绿色的部分,更进一步,\(x,y\) 这两个位置,至少有一个位置是其所属区间的最小值,不失一般性地,假设 \(x\) 为其区间的最小值,那么有 \(a_x\) 比所有蓝色部分更小,那么对于红色区间最小值出现的地方,我们分情况讨论:
- 当红最小值出现在绿色部分时,如果 \(k\leftarrow k+1\),那么此时整个区间的最小值为 \(b'_i=b_i=a_x=\min\{b_i,b_{i+1}\}\);
- 当红最小值在 \(y\) 上,当 \(k\leftarrow k+1\) 时,蓝色区间会将 \(y\) 包住,这个时候 \(b'_i=\min\{a_x,a_y\}=\min\{b_i,b_{i+1}\}\);
综上,当 \(k\ge 2\) 时,如果有某个 \(\{b_i\}\) 是一个 \(1\sim n-k+1\) 的排列,那么当 \(k\) 增大时,\(b'=\{\min\{b_1,b_2\},\min\{b_2,b_3\},\min\{b_3,b_4\},...,\min\{b_{k-1},b_k\}\}\),显然,这变成了一个 \(1\sim n-k\) 的排列。
至于为什么 \(k=1\) 不行?因为绿色的部分消失了,两个区间没有绝对的关联了。
关于官方题解
对于 \(1<k<n\) 的情况,\(k\) 压缩应该包含恰好一次 \(1\),但 \(1\) 是最小的数,所以它应该出现在左端点或右端点,不失一般性地假设其位于 \(n\),那么 \(a[1:n-1]\) 的 \(k\) 压缩应该是一个 \(2,3,4,...,n-1\) 的排列,而这是子问题,可以迭代求解。
那么,我们可以使用这样的算法求解:维护区间 \([l,r]\),初始 \(l=1,r=n\),然后迭代 \(i=1,2,3,...,n\),对于每个 \(i\),我们确保 \(a_l=i\;\or\;a_r=i\),并相应移动 \(l\) 或 \(r\) 指针,然后我们检查 \(\min_{j=l}^r a_j=i+1\).
如果 \(i\) 是第一个失败的,那么对于所有 \(2\le k\le n-i+1\) 都是 \(0\),而以后都为 \(1\).
这实际上也从侧面说明的答案的单调性。
叁、参考代码 ¶
唔,\(\mathcal O(n\log n)\) 也算过了吧,那我贴这里了:
#include<cstdio>
#include<vector>
#include<cstring>
#include<algorithm>
#include<set>
using namespace std;
// #define NDEBUG
#include<cassert>
namespace Elaina{
#define rep(i, l, r) for(int i=(l), i##_end_=(r); i<=i##_end_; ++i)
#define drep(i, l, r) for(int i=(l), i##_end_=(r); i>=i##_end_; --i)
#define fi first
#define se second
#define mp(a, b) make_pair(a, b)
#define Endl putchar('\n')
#define mmset(a, b) memset(a, b, sizeof a)
// #define int long long
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int, int> pii;
typedef pair<ll, ll> pll;
template<class T>inline T fab(T x){ return x<0? -x: x; }
template<class T>inline void getmin(T& x, const T rhs){ x=min(x, rhs); }
template<class T>inline void getmax(T& x, const T rhs){ x=max(x, rhs); }
template<class T>inline T readin(T x){
x=0; int f=0; char c;
while((c=getchar())<'0' || '9'<c) if(c=='-') f=1;
for(x=(c^48); '0'<=(c=getchar()) && c<='9'; x=(x<<1)+(x<<3)+(c^48));
return f? -x: x;
}
template<class T>inline void writc(T x, char s='\n'){
static int fwri_sta[1005], fwri_ed=0;
if(x<0) putchar('-'), x=-x;
do fwri_sta[++fwri_ed]=x%10, x/=10; while(x);
while(putchar(fwri_sta[fwri_ed--]^48), fwri_ed);
putchar(s);
}
}
using namespace Elaina;
const int maxn=3e5;
const int logn=18;
bool yes[maxn+5];
int a[maxn+5], n;
int st[maxn+5][logn+5];
int lgg[maxn+5], pow2[logn+5];
inline void buildst(){
rep(i, 1, n) st[i][0]=a[i];
rep(j, 1, logn) rep(i, 1, n-pow2[j-1])
st[i][j]=min(st[i][j-1], st[i+pow2[j-1]][j-1]);
}
inline int query(int l, int r){
int tmp=lgg[r-l+1];
return min(st[l][tmp], st[r-pow2[tmp]+1][tmp]);
}
inline bool check(int x){
rep(i, 1, n) yes[i]=0;
rep(i, x, n){
int cur=query(i-x+1, i);
// printf("query(%d, %d) == %d\n", i-x+1, x, query(i-x+1, x));
if(yes[cur]) return false;
yes[cur]=1;
}
rep(i, 1, n-x+1) if(!yes[i]) return false;
return 1;
}
signed main(){
lgg[0]=-1, pow2[0]=1;
rep(i, 1, maxn) lgg[i]=lgg[i>>1]+1;
rep(i, 1, logn) pow2[i]=pow2[i-1]<<1;
rep(_, 1, readin(1)){
n=readin(1);
rep(i, 1, n) a[i]=readin(1);
buildst();
int l=2, r=n, mid, ans=n+1;
while(l<=r){
mid=(l+r)>>1;
if(check(mid)) ans=mid, r=mid-1;
else l=mid+1;
}
rep(i, 1, n) yes[i]=0;
int spec=1;
rep(i, 1, n) if(yes[a[i]]) spec=0;
else yes[a[i]]=1;
if(spec) putchar('1');
else putchar('0');
rep(i, 2, ans-1) putchar('0');
rep(i, ans, n) putchar('1');
Endl;
}
return 0;
}
肆、关键之处 ¶
还是递归处理子问题啊,为什么就是看不出来呢?或者说对于问题并没有分析相邻俩 \(k\) 都合法的关系?

