[CF1450C2]Errich-Tac-Toe (Hard Version)

壹、题目描述 ¶

传送门 to Luogu.

贰、题解 ¶

飞雪连天射 \(\rm C1\)，却见弯弓跪 \(\rm C2\)，自 \(\rm C1\) 使用一种奇怪的旋转填法过掉后，我始终认为 \(\rm C2\) 也是可以这样做的，然而事实是

然而我将剩下的所有事件都拿来肝 \(D\)，还是差点时间优化......

事实上，我的 \(\rm C1\) 做法并不能拓展到 \(\rm C2\)，想要做 \(\rm C2\) 还需另寻他路。

这种问题，显然是要对这个格子图染色，结合经典的做法，我们对于 \((i+j)\bmod 3\) 的余数入手进行染色，然后我们可以得到这样的图：

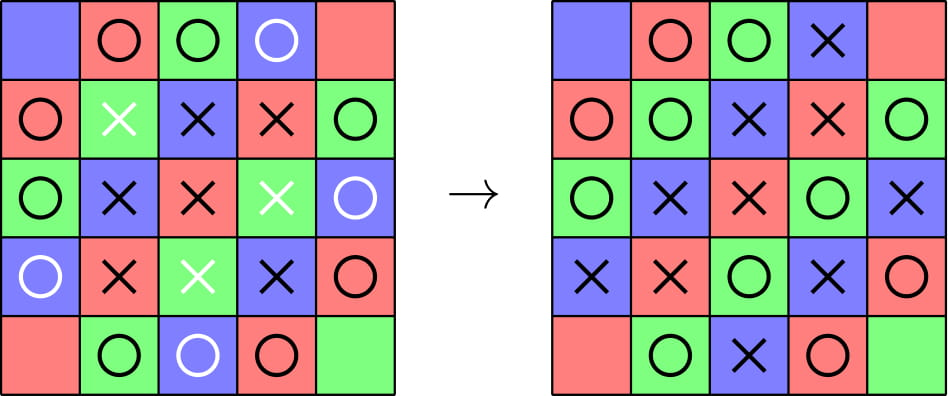
如果有这样一张表：

\(\rm Character\)\\((i+j)\bmod 3\)	\(0\)	\(1\)	\(2\)
\(X\)	\(x_0\)	\(x_1\)	\(x_2\)
\(O\)	\(o_0\)	\(o_1\)	\(o_2\)

那首先有 \(k=x_0+x_1+x_2+o_0+o_1+o_2\). 如果令 \(a_{ij}=x_i+o_j\)，那么就有

\[a_{01}+a_{02}+a_{10}+a_{12}+a_{20}+a_{21}=2k \]

显然，就会存在

\[\min\{a_{01},a_{02},a_{10},a_{12},a_{20},a_{21}\}\le \left\lfloor{2k\over 6}\right\rfloor \]

找到最小值，并替换即可。不过这真的是人类智慧吗......我并不觉得这方法很容易想到。

叁、参考代码 ¶

#include<cstdio>
#include<vector>
#include<cstring>
#include<algorithm>
using namespace std;

// #define NDEBUG
#include<cassert>

namespace Elaina{
    #define rep(i, l, r) for(int i=(l), i##_end_=(r); i<=i##_end_; ++i)
    #define drep(i, l, r) for(int i=(l), i##_end_=(r); i>=i##_end_; --i)
    #define fi first
    #define se second
    #define mp(a, b) make_pair(a, b)
    #define Endl putchar('\n')
    #define mmset(a, b) memset(a, b, sizeof a)
    // #define int long long
    typedef long long ll;
    typedef unsigned long long ull;
    typedef pair<int, int> pii;
    typedef pair<ll, ll> pll;
    template<class T>inline T fab(T x){ return x<0? -x: x; }
    template<class T>inline void getmin(T& x, const T rhs){ x=min(x, rhs); }
    template<class T>inline void getmax(T& x, const T rhs){ x=max(x, rhs); }
    template<class T>inline T readin(T x){
        x=0; int f=0; char c;
        while((c=getchar())<'0' || '9'<c) if(c=='-') f=1;
        for(x=(c^48); '0'<=(c=getchar()) && c<='9'; x=(x<<1)+(x<<3)+(c^48));
        return f? -x: x;
    }
    template<class T>inline void writc(T x, char s='\n'){
        static int fwri_sta[1005], fwri_ed=0;
        if(x<0) putchar('-'), x=-x;
        do fwri_sta[++fwri_ed]=x%10, x/=10; while(x);
        while(putchar(fwri_sta[fwri_ed--]^48), fwri_ed);
        putchar(s);
    }
}
using namespace Elaina;

const int maxn=300;

char c[maxn+5][maxn+5];
int n;

int a[5][5];

inline void geta(){
    memset(a, 0, sizeof a);
    for(int i=0; i<n; ++i){
        for(int j=0; j<n; ++j) if(c[i][j]!='.'){
            int cur=(i+j)%3;
            if(c[i][j]=='X') rep(t, 0, 2) ++a[cur][t];
            else rep(t, 0, 2) ++a[t][cur];
        }
    }
}

signed main(){
    rep(_, 1, readin(1)){
        n=readin(1);
        for(int i=0; i<n; ++i) scanf("%s", c[i]);
        geta();
        int minn=n*n, x, y;
        rep(i, 0, 2) rep(j, 0, 2) if(i!=j){
            if(a[i][j]<minn)
                minn=a[i][j], x=i, y=j;
        }
        for(int i=0; i<n; ++i) for(int j=0; j<n; ++j) if(c[i][j]!='.'){
            int cur=(i+j)%3;
            /** fill in the opposite color */
            if(cur==x) c[i][j]='O';
            else if(cur==y) c[i][j]='X';
        }
        for(int i=0; i<n; ++i) printf("%s\n", c[i]);
    }
    return 0;
}

肆、关键之处 ¶

这个构造方法......只能说 “限制可能会给人以提示” 了罢......另外可能就只有 \((i+j)\bmod 3\) 的余数这方面可以想到了。