[CF1131G]Most Dangerous Shark
壹、题目描述 ¶
有 \(n(n\le 10^7)\) 个骨牌,相邻距离为 \(1\),对于第 \(i\) 个骨牌,其高度为 \(h_i\),推倒它的花费为 \(c_i\),你可以选择将它向左或向右推倒,当第 \(i\) 个骨牌被推倒时,它会以相同方向推倒与其距离 小于 \(h_i\) 的骨牌,求推倒所有骨牌的最小花费。
贰、题解 ¶
设 \(f_i\) 表示推倒前 \(i\) 个骨牌的最小花费,那么有
其中,\(L_i\) 表示将第 \(i\) 个骨牌向左推倒,最远能到的点,\(R_i\) 类似。这个转移实际上讨论了两种情况 —— 当前骨牌是自己倒,还是被别人推倒。不过问题在于,这个转移是 \(\mathcal O(n^2)\) 的,并且,还有一个问题,如何快速求出 \(L,R\) ?
无法走下去,那么我们就要进行一些观察......
Observation#0
如果第 \(i\) 个牌能够推倒第 \(i-1\) 个牌,那么 \(L_i\le L_{i-1}\),即一定会推得更远一些,对于 \(R\) 有相同的性质。
从图上来说,就是多个 “弧”,一个包着一个,普遍地,两个 “弧” 的关系不是包含就是相离。

知道这个东西,求 \(L_i\) 与 \(R_i\) 就很好办了,我们只需要使用栈,每次判断栈顶是否能够包含当前的点,如果不能,那么栈顶的边界就在当前点之前。
对于答案的计算,事实上,转移式中 \(j<i\le R_j\) 也有类似的性质,即,包含点 \(i\) 的弧一定是一个套着一个向外的
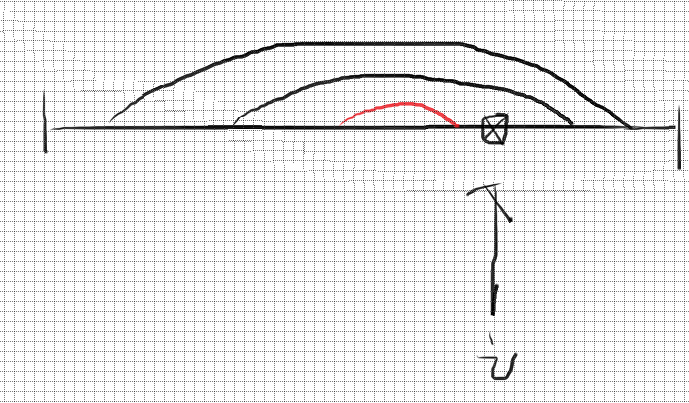
当然,我们的栈顶元素不一定会包含 \(i\),所以我们还要判断是否能够包含 \(i\),如果不能,那么就弹掉。
总而言之,这个栈的关键就在于,栈顶的 \(f_x+c_{x+1}\) 是最小的,但是是最有可能不满足条件的;而栈底不一定 \(f_y+c_{y+1}\) 最优,但是能够覆盖的最广。
都是用的栈,时间复杂度就只有 \(\mathcal O(n)\) 了。
叁、参考代码 ¶
#include<cstdio>
#include<vector>
#include<cstring>
#include<algorithm>
#include<vector>
using namespace std;
// #define NDEBUG
#include<cassert>
namespace Elaina{
#define rep(i, l, r) for(int i=(l), i##_end_=(r); i<=i##_end_; ++i)
#define drep(i, l, r) for(int i=(l), i##_end_=(r); i>=i##_end_; --i)
#define fi first
#define se second
#define mp(a, b) make_pair(a, b)
#define Endl putchar('\n')
#define mmset(a, b) memset(a, b, sizeof a)
// #define int long long
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int, int> pii;
typedef pair<ll, ll> pll;
template<class T>inline T fab(T x){ return x<0? -x: x; }
template<class T>inline void getmin(T& x, const T rhs){ x=min(x, rhs); }
template<class T>inline void getmax(T& x, const T rhs){ x=max(x, rhs); }
template<class T>inline T readin(T x){
x=0; int f=0; char c;
while((c=getchar())<'0' || '9'<c) if(c=='-') f=1;
for(x=(c^48); '0'<=(c=getchar()) && c<='9'; x=(x<<1)+(x<<3)+(c^48));
return f? -x: x;
}
template<class T>inline void writc(T x, char s='\n'){
static int fwri_sta[1005], fwri_ed=0;
if(x<0) putchar('-'), x=-x;
do fwri_sta[++fwri_ed]=x%10, x/=10; while(x);
while(putchar(fwri_sta[fwri_ed--]^48), fwri_ed);
putchar(s);
}
}
using namespace Elaina;
const int maxn=250000;
const int maxm=1e7;
int n, m;
int k[maxn+5];
vector<int>a[maxn+5], v[maxn+5];
int h[maxm+5], cnt; ll c[maxm+5];
inline void input(){
n=readin(1), m=readin(1);
rep(i, 1, n){
k[i]=readin(1);
rep(j, 1, k[i]) a[i].push_back(readin(1));
rep(j, 1, k[i]) v[i].push_back(readin(1));
}
int id, mul, q=readin(1);
rep(i, 1, q){
id=readin(1), mul=readin(1);
rep(j, 0, k[id]-1){ ++cnt;
h[cnt]=a[id][j], c[cnt]=1ll*v[id][j]*mul;
}
}
// Endl;
// rep(i, 1, m) printf("%d %lld\n", h[i], c[i]);
}
int L[maxm+5], R[maxm+5];
int sta[maxm+5], ed;
inline void getLR(){
rep(i, 1, m){
while(ed && sta[ed]+h[sta[ed]]<=i)
R[sta[ed]]=i-1, --ed;
sta[++ed]=i;
}
while(ed) R[sta[ed--]]=m;
drep(i, m, 1){
while(ed && i+h[sta[ed]]<=sta[ed])
L[sta[ed]]=i+1, --ed;
sta[++ed]=i;
}
while(ed) L[sta[ed--]]=1;
// rep(i, 1, m) printf("pos %d :> L == %d, R == %d\n", i, L[i], R[i]);
}
ll f[maxm+5];
inline void getf(){
rep(i, 1, m){
f[i]=f[L[i]-1]+c[i]; // push it
while(ed && R[sta[ed]]<i) --ed;
if(ed) getmin(f[i], f[sta[ed]-1]+c[sta[ed]]);
if(!ed) sta[++ed]=i;
else if(f[i-1]+c[i]<f[sta[ed]-1]+c[sta[ed]])
sta[++ed]=i;
}
writc(f[m]);
}
signed main(){
input();
getLR();
getf();
return 0;
}
肆、关键之处 ¶
单调栈和单调队列,重要的是两单调:
- 加入时间单调:队列的是队头最早,栈是栈顶最晚。
- 答案单调:取头一定最优,只是有可能不合法。

