[CF1511E]Colorings and Dominoes
壹、题目描述 ¶
贰、题解 ¶
我已经完全学懂概率与期望啦. 明白了基础不牢带给人的无限困扰。
首先明白题目的机制,大概可以表示成下面的图:
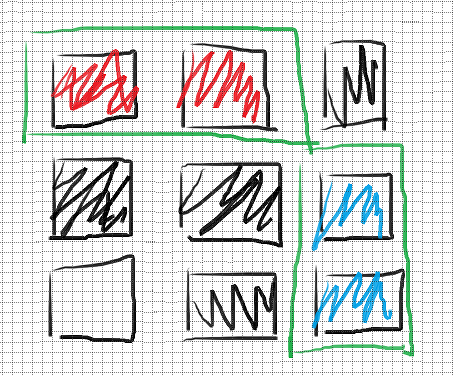
将格子涂红,影响到的是横着放的多米诺骨牌数量;将格子涂蓝,影响到的是竖着放的多米诺骨牌数量,因此,我们可以横竖分开考虑。( 虽然这句话我看了 \(10min\) 才想出来 😦 )
现在,我们面临的问题就是,面对一排白色的格子(假设一共有 \(x\) 个),对于 \(2^x\) 中染色方案的每一种,最多放置多米诺牌数量之和。这个问题乍一看很简单,然而我为了攻克这个问题想了很多种方法 然而都被叉掉了
直接计数我不会,因为我认为状态设计似乎很困难 —— 我想要设计 \(f_i\) 表示对于长度为 \(i\) 的连续白格子,所有方案能放下的多米诺骨牌数量之和,那么转移就是讨论结尾的白格子的状态了,蓝色,红色,或者红色且与前一个匹配,但是我又想到,对于每一种染色方案,我所钦定的染色可能并不是能放下最多骨牌的染色方法。
然后我想到了 “概率期望在计数问题中的应用”,十分自然想到了一个多米诺骨牌能够在位置 \(i\) 被放下的概率是多少,然后我设计了一个自认为正确的概率转移,并付诸实践,结果是除了第一组样例以外都可以过,在接下来的讨论中,\(\sf XJX\) 把我叉掉了,而且理由十分显然......
下面介绍几种解决这个问题的方法。
Method# 1
第一种方法,设 \(f_i\) 表示除了当前我们考虑的两个格子以外,前面剩下的白格子有 \(i\) 个的情况下,骨牌一定放在当前俩格子上的概率,首先,我们可以计算出 \(f_0={1\over 4}\),这是显然的,因为我们想要让两个白格同时为红色。
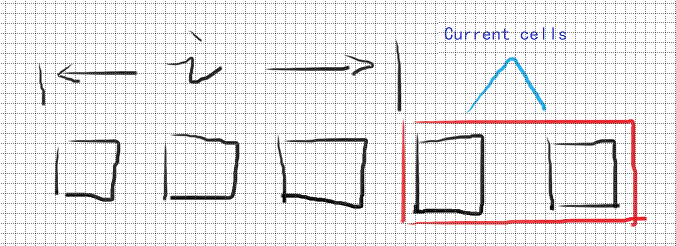
考虑 \(f_1\),由于我们想要让骨牌一定放到当前的两个格子上,所以首先我们要有 \(1\over 4\),当前两个格子为红色的,但是由一种是不行的,那就是这三个都是红色的情况 —— 因为骨牌可能跑到前面去,这个概率是 \(1\over 8\),所以就有 \(f_1={1\over 4}-{1\over 8}\).
继续考虑 \(f_2\),其概率为 \({1\over 4}-{1\over 8}+{1\over 16}\),当前两格子红色,减去三个为红色的,而四个都是红色的也可以。
对于 \(f_n\),事实上有
\[f_n=\sum_{i=0}^n(-1)^i\left({1\over 2}\right)^{i+2}=f_{i-1}+(-1)^n\left({1\over 2}\right)^{n+2} \]这个东西事实上是个容斥,容斥前面有白色格子的数量,即前面至少有几个白色格子,后面的递推式只是取巧而已,但是它的确可以帮助我们做到线性递推,然后 \(\mathcal O(nm)/\mathcal O(nm\log p)\) 解决问题。
事实上我在改进自己的 ** 概率转移后得到了这个东西,发现与官解不谋而合。
Method# 2
另一种方法来自 \(\sf XJX\),定义 \(g_{i,0|1}\) 表示当前这个格子是一个牌的左边还是右边,递推式有
\[g_{i,0}=\left(g_{i-1,1}+{1\over 2}\right)\times {1\over 2} \\ g_{i,1}={1\over 2}\times g_{i-1,0} \]递推式十分好理解。使用也很类似。
Method# 3
这一种方法来自 \(\sf sister\),祂做到了直接推方案数。定义 \(h_i\) 表示有 \(i\) 个白格时候的方案数,存在递推式
\[h_i=2h_{i-2}+2^{i-2}+h_{i-1} \]这个递推式成立的基础来源于一种经典贪心 —— 树上配对。
考虑结尾两个都是红色,由于经典贪心,让他们两个配对是可以达到最优的,这个方案是 \(h_{i-2}+2^{i-2}\).
当 \(i-1\) 是蓝色,那么 \(i\) 也得单出来了,贡献 \(h_{i-2}\).
如果 \(i\) 是蓝色,贡献就是 \(h_{i-1}\).
把他们三个加起来,得到上面的线性递推式子。
前两种方法都能很好解决概率的问题,但是 \(\sf closestool\) 就不这么认为了,祂认为使用概率是蠢笨的人的做法,而神不应该这样做,祂使用了一种不怎么需要推概率的方法,你可以直接去祂的博客看,或者我把祂的题解附在下面了。
*Method# 4
这里提供一个不同的思路 我们考虑对于每对相邻的位置,单独地计算它的贡献 先只考虑横着的情况 我们发现只有当钦定的方格两旁红色格子数同偶时才会计入答案,贡献 \(1\)(\((RR)\underline{(RR)}(RR)\)),而异奇偶时贡献 \(1\over 2\)(\((O\underline{(RR)}(RR)\)与 \((R\underline{R)O}(RR)\) 同样为最大答案),而同奇时不计入答案(\((R\underline{R)(R}R)\)),所以设此对格子 \((x,y)(x,y+1)\) 左右能延伸到的最长空位(含自己)分别为\(L,R\) 对于每种情况单独维护,先考虑同偶时贡献(设总空位数为\(cnt\)):
\[\sum_{i=2k+1,i\in[1,L]}\sum_{j=2t+1,j\in[1,R]}2^{cnt-i-j-[i\not= L]-[j\not =R]} \]为什么呢?因为我们相当于枚举了这段红块的长度,而红块的两旁需要为空或者蓝色,直接操作发现是\(O((nm)^3)\)的,考虑优化
\[\sum_{i=2k+1,i\in[1,L]}\sum_{j=2t+1,j\in[1,R]}2^{cnt-i-j-[i\not= L]-[j\not =R]} \\=2^{cnt}\left(\sum_{i=2k+1,i\in[1,L]}2^{-i-[i\not= L]}\right)\left(\sum_{j=2t+1,j\in[1,R]}2^{-j-[j\not =R]}\right) \]这里已经是 \(O(nm(n+m))\) 了,因为发现遍历过程中每次只会 \(++L,--R\) 以及在每一空段的开头 \(\mathcal O(len)\) 地处理,所以每次移动只会更改 \(sigma\) 内 \(2\) 项的值,可以动态维护括号内的累和,这样时间复杂度 \(O(nm)\),这里由于赛时敲傻了,所以打的比较复杂,实际上可以非常简单的。
打上 '*' 的原因是这个方法是神的馈赠。
叁、参考代码 ¶
然而只有第一种方法的代码,另外两种可以直接去找它们的发明者。
另,由于笔者太懒,只在考场烂尾代码上改了一点关于递推 \(f\) 的细节 😃,复杂度 \(\mathcal O(nm\log p)\).
#include<cstdio>
#include<vector>
#include<cstring>
#include<algorithm>
#include<map>
using namespace std;
// #define NDEBUG
#include<cassert>
namespace Elaina{
#define rep(i, l, r) for(int i=(l), i##_end_=(r); i<=i##_end_; ++i)
#define drep(i, l, r) for(int i=(l), i##_end_=(r); i>=i##_end_; --i)
#define fi first
#define se second
#define mp(a, b) make_pair(a, b)
#define Endl putchar('\n')
#define mmset(a, b) memset(a, b, sizeof a)
// #define int long long
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int, int> pii;
typedef pair<ll, ll> pll;
template<class T>inline T fab(T x){ return x<0? -x: x; }
template<class T>inline void getmin(T& x, const T rhs){ x=min(x, rhs); }
template<class T>inline void getmax(T& x, const T rhs){ x=max(x, rhs); }
template<class T>inline T readin(T x){
x=0; int f=0; char c;
while((c=getchar())<'0' || '9'<c) if(c=='-') f=1;
for(x=(c^48); '0'<=(c=getchar()) && c<='9'; x=(x<<1)+(x<<3)+(c^48));
return f? -x: x;
}
template<class T>inline void writc(T x, char s='\n'){
static int fwri_sta[1005], fwri_ed=0;
if(x<0) putchar('-'), x=-x;
do fwri_sta[++fwri_ed]=x%10, x/=10; while(x);
while(putchar(fwri_sta[fwri_ed--]^48), fwri_ed);
putchar(s);
}
}
using namespace Elaina;
const int maxn=3e5;
const int mod=998244353;
inline int qkpow(int a, int n){
int ret=1;
for(; n; n>>=1, a=1ll*a*a%mod)
if(n&1) ret=1ll*ret*a%mod;
return ret;
}
char s[maxn+5];
vector< vector<bool> >a;
int n, m, U;
inline void input(){
n=readin(1), m=readin(1);
a.resize(n);
for(int i=0; i<n; ++i){
a[i].resize(m);
scanf("%s", s);
for(int j=0; j<m; ++j){
a[i][j]=(s[j]=='o');
U+=a[i][j];
}
}
}
int pow2[maxn+5], f[maxn+5];
#define sign(i) (((i)&1)? -1: 1)
inline void init(){
pow2[0]=1;
rep(i, 1, maxn+2) pow2[i]=(pow2[i-1]<<1)%mod;
f[0]=qkpow(4, mod-2);
rep(i, 1, maxn) f[i]=(f[i-1]+mod+1ll*sign(i)*qkpow(pow2[i+2], mod-2)%mod)%mod;
}
inline void getans(){
int ans=0;
for(int i=0; i<n; ++i){
int cur;
for(int j=0; j<m; j=cur+1){
cur=j;
if(a[i][j]==1){
while(cur<m-1 && a[i][cur+1]==1) ++cur;
int x=cur-j+1;
for(int k=j+1; k<=cur; ++k)
ans=(ans+1ll*pow2[U]*f[k-j-1]%mod)%mod;
}
}
}
for(int j=0; j<m; ++j){
int cur;
for(int i=0; i<n; i=cur+1){
cur=i;
if(a[i][j]==1){
while(cur<n-1 && a[cur+1][j]==1) ++cur;
int x=cur-i+1;
for(int k=i+1; k<=cur; ++k)
ans=(ans+1ll*pow2[U]*f[k-i-1]%mod)%mod;
}
}
}
writc(ans);
}
signed main(){
input();
init();
getans();
return 0;
}
肆、关键的地方 ¶
横竖相互无关,可以分开算,这是第一个关键点。
计数问题可以从合法方案概率入手,这是第二个关键点。
然而即使想清楚了这两个关键仍然没有切掉这道题:(


