[CF1450H1]Multithreading (Easy Version)
壹、题目描述 ¶
贰、题解 ¶
这东西我是一辈子都想不到的,即使我能够贪心出一点结论,也不会知道具体地数学表示。
若没有 \(\tt ?\),设 \(B_o\) 为奇数位置 \(\tt b\) 的个数,\(B_e\) 为偶数位置 \(\tt b\) 的个数,类似地定义 \(W_o,W_e\),那么,我们有:
我是真不可能想到这个结论,但是这的确可以证明。
注:如果你已经会证明了,则可以跳过证明部分。
不失普遍性地,我们假设 \(B_o\ge B_e\),令 \(2k=B_o-B_e\),证明分成两个部分:\(f(c)\le k\) 以及 \(f(c)\ge k\).
Proof Part#1
证明 \(f(c)\le k\),即答案的上界为 \(k\).
首先,贪心地将最近的且奇偶性不同的同色点连接,由于 \(B_o>B_e\;\and\;B_o-B_e=2k\),那么会在奇数位置剩下 \(2k\) 的黑色点,同样的,会在偶数位置剩下 \(2k\) 个白色点,即我们这样连:
有两个重要性质: 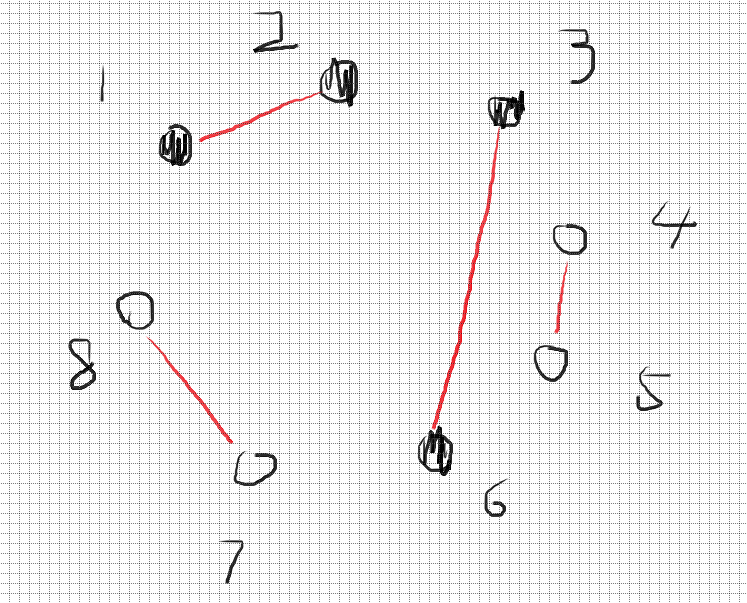
- 两个点围成的两个部分没有和他们颜色相同且没有被匹配的点,假设存在这样的点,那么它的下标一定会是奇数或偶数,而我们两个端点一奇一偶,那么它一定可以和其中一个端点构成更近的匹配;
- 两个点分开的两个部分,其内部的点一定都是偶数,这比较显然吧;
此时我们证明了这些点都是同色,并且个数还是偶数,那么他们一定可以内部搞定而不会连出去。即这一步操作不会产生异色交点。我们可以把这些部分都忽略了,因为外部的连接无论如何都不会影响到他们了。
接下来,剩下的点一定都是这种情况(将已经连接的部分忽略了)
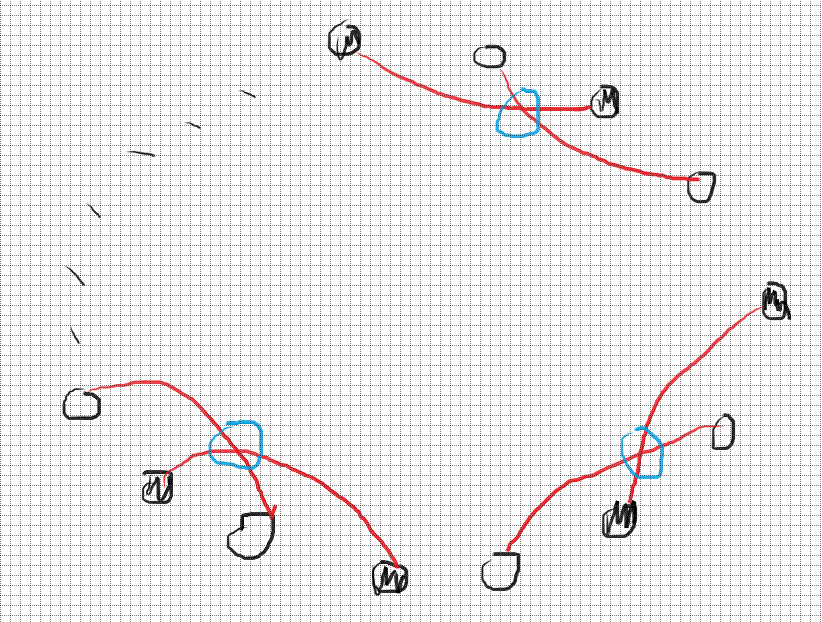
由于有 \(2k\) 个黑色的,并且我们发现每两个会产生一个异色交点,故总共就会有 \(k\) 个交点,由于这个构造是普适性的,任意一种情况都会存在这样一种构造,所以答案绝不会超过 \(k\),即答案至多为 \(k\).
Proof Part#2
证明 \(f(c)\ge k\),即答案至少为 \(k\),此时我们应该考虑最少的交点次数都至少为 \(k\).
此处需要使用以下结论:
最优构造中可以不存在同色交点。即在最优构造中,同色交点一定可以被避免。
为什么呢?我们对比一下两种连法:
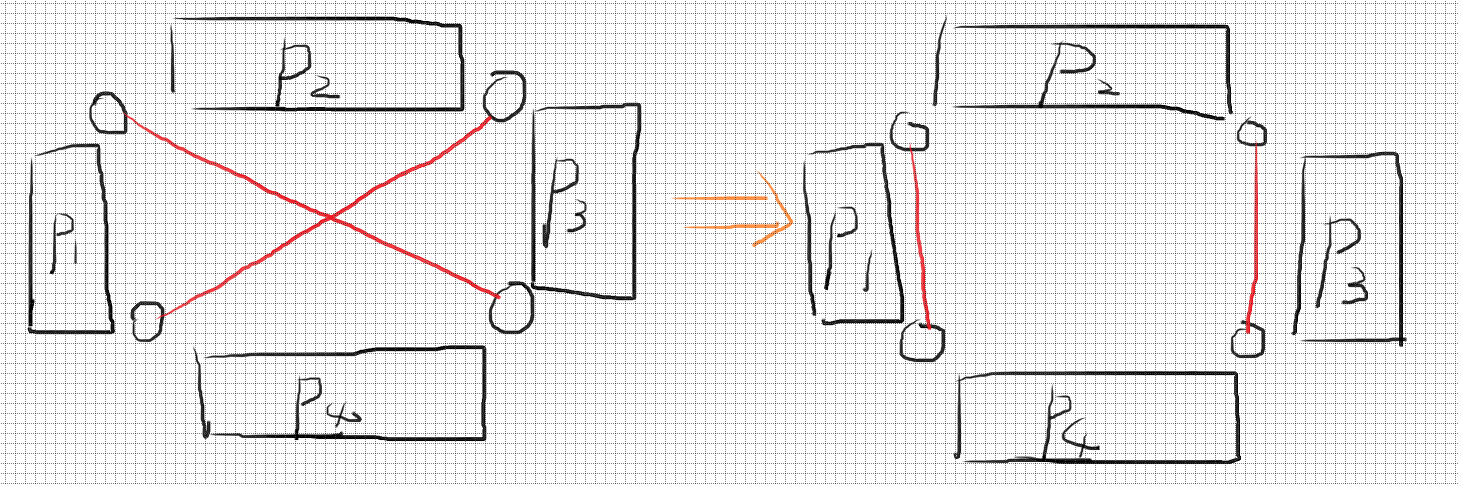
第一种方法存在同色交点,而如果我们将其变成第二种,我们发现,异色交点不可能会增多,而只有可能减少,具体减少的是从 \(P_2\) 到 \(P_4\) 的连边与两个白色边形成的交点,而这又是最优情况,所以减少也不可能减少。
故而这种调整不会改变异色交点个数,类似地,我们可以将所有同色交点都打开。
由于 \(B_o-B_e=2k\),所以一定会有 \(k\) 条奇偶性相同的边,而每连这样一条边,将原图分成的两个部分一定点数都为奇数,为奇数则一定会有左部分和右部分的一条边,这条边一定会和我们的分割边产生一个交点,这种交点显然不可避免,然而我们又证明最优构造中同色交点一定可以避免,所以这种交点不可能是同色交点,只有可能为异色交点。
而每一条分割边至少一个这样的交点,有 \(k\) 条,自然而然至少 \(k\) 个异色交点。
上下界都是 \(k\),所以 \(f(c)=k={1\over 2}|B_o-B_e|\).
\(\blacksquare.\)
考虑如何计数。设 \(F\) 为 \(\tt ?\) 的集合,类似定义 \(F_o,F_e\),我们首先枚举 \(F\) 的子集 \(i\),并强制将 \(i\) 中偶数位置填 \(\tt b\),奇数位置填 \(\tt w\),对于 \(\complement_Fi\),我们将偶数位置填 \(\tt w\),奇数位置填 \(\tt b\),那么,就有
注意到 \(B_o+|F_o|={n\over 2}-W_o\),我们令 \(x=B_o+|F_o|-B_e={n\over 2}-W_o-B_e\),那么
由于 \(i\) 对应的方案有 \({|F|\choose i}\) 种,故而总方案的期望值为
刚开始是 \(2^{|F|-1}\) 的原因是我们要保证 \(i\) 为 奇数/偶数。
时间复杂度 \(\mathcal O(n)\).
叁、参考代码 ¶
#include<cstdio>
#include<vector>
#include<cstring>
#include<algorithm>
using namespace std;
// #define NDEBUG
#include<cassert>
namespace Elaina{
#define rep(i, l, r) for(int i=(l), i##_end_=(r); i<=i##_end_; ++i)
#define drep(i, l, r) for(int i=(l), i##_end_=(r); i>=i##_end_; --i)
#define fi first
#define se second
#define mp(a, b) make_pair(a, b)
#define Endl putchar('\n')
#define mmset(a, b) memset(a, b, sizeof a)
// #define int long long
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int, int> pii;
typedef pair<ll, ll> pll;
template<class T>inline T fab(T x){ return x<0? -x: x; }
template<class T>inline void getmin(T& x, const T rhs){ x=min(x, rhs); }
template<class T>inline void getmax(T& x, const T rhs){ x=max(x, rhs); }
template<class T>inline T readin(T x){
x=0; int f=0; char c;
while((c=getchar())<'0' || '9'<c) if(c=='-') f=1;
for(x=(c^48); '0'<=(c=getchar()) && c<='9'; x=(x<<1)+(x<<3)+(c^48));
return f? -x: x;
}
template<class T>inline void writc(T x, char s='\n'){
static int fwri_sta[1005], fwri_ed=0;
if(x<0) putchar('-'), x=-x;
do fwri_sta[++fwri_ed]=x%10, x/=10; while(x);
while(putchar(fwri_sta[fwri_ed--]^48), fwri_ed);
putchar(s);
}
}
using namespace Elaina;
const int maxn=2e5;
const int mod=998244353;
const int inv2=499122177;
inline int qkpow(int a, int n){
int ret=1;
for(; n; n>>=1, a=1ll*a*a%mod)
if(n&1) ret=1ll*ret*a%mod;
return ret;
}
int fac[maxn+5], finv[maxn+5];
int n, m, b[2], w[2], f[2];
char s[maxn+5];
inline void init(){
fac[0]=1;
rep(i, 1, maxn) fac[i]=1ll*fac[i-1]*i%mod;
finv[maxn]=qkpow(fac[maxn], mod-2);
drep(i, maxn-1, 1) finv[i]=1ll*finv[i+1]*(i+1)%mod;
finv[0]=1;
}
inline int C(int n, int m){
if(n<m) return 0;
return 1ll*fac[n]*finv[m]%mod*finv[n-m]%mod;
}
inline void input(){
n=readin(1), m=readin(1);
scanf("%s", s+1);
rep(i, 1, n){
if(s[i]=='b') ++b[i&1];
else if(s[i]=='w') ++w[i&1];
else ++f[i&1];
}
}
inline void calc(){
int x=(n>>1)-w[1]-b[0], ans=0;
rep(i, 0, f[0]+f[1]) if((i&1)==(x&1))
ans=(ans+1ll*fab(i-x)%mod*C(f[0]+f[1], i)%mod)%mod;
ans=1ll*ans*qkpow(inv2, f[0]+f[1])%mod;
writc(ans);
}
signed main(){
init();
input();
calc();
return 0;
}


