[CF1450G]Communism
壹、题目描述 ¶
贰、题解 ¶
看到这个题目限制就觉得恶心了。
应该敏锐地注意到,除去不出现的,我们剩下的 \(26-6=20\) 个字符刚好是状压的范围,然后,我们就用状压。
既然最终只有一种字符 \(\tt z\),那么上一步,就是把另一种字符的所有位置进行操作,而这些位置原本是除了 \(\tt z\) 以外的其它字符位置的并集。倒推回去,中间状态就是把一个字符集 \(S\) 进行操作,此时字符集 \(S\) 中所有字符的所有原先位置上,都有着相同的字符(该字符是什么不重要)。—— \(\sf Principal\)
定义 \(len_S\) 为字符集 \(S\) 的左右端点围起来的长度,\(cnt_S\) 为字符集 \(S\) 中所有字符出现的次数,\(l_S,r_S\) 分别为左右端点,那么一个字符集能够被操作的限制即 \(k\times len_S\le cnt_S\),对于这个 \(k\),我们可以形象地理解为 \(S\) 在其围起来的区间中的限制浓度,达到这个限制浓度我们就可以操作它。对于这种集合,我们称其为可操作的。
考虑定义 \(dp_S\) 表示字符集 \(S\) 能否被操作,转移就有如下:
- \(dp_0=1\),空集显然可以被操作;
- 对于只有一种字符的字符集,我们可以将其作为边界特殊处理;
- 如果 \(S\) 有两个子集 \(S_1,S_2\;\text{s.t.}\;S_1\cup S_2=S\;\and\;S_1\cap S_2=\emptyset\),若 \(dp_{S_1}=1\;\and\;dp_{S_2}=1\),那么 \(dp_S=1\);
- 对于 \(S\) 中的任意一种字符 \(\tt x\),如果 \(dp_{S\oplus x}=1\),并且 \(S\) 集合是可操作的,那么 \(dp_S=1\);
后俩东西事实上就是 \(\rm DP\) 转移了,但是这样复杂度为 \(\mathcal O(3^{|\Sigma|})\),因为对于第一种转移,我们需要枚举 \(S\) 的所有子集。
但是事实上是没有必要所有都枚举的,对于两个子集 \(S_1,S_2\),我们实际上只需要 \(r_{S_1}<l_{S_2}\) 或者 \(l_{S_1}>r_{S_2}\) 的情况。
对于两个子集的区间有交集的情况,我们一定可以对其中一个子集进行一些操作,使其所有字符都变成另一个集合的一些字符,这个时候另一个子集是一定可以操作的,由 “浓度” 方向我们可以很好理解。
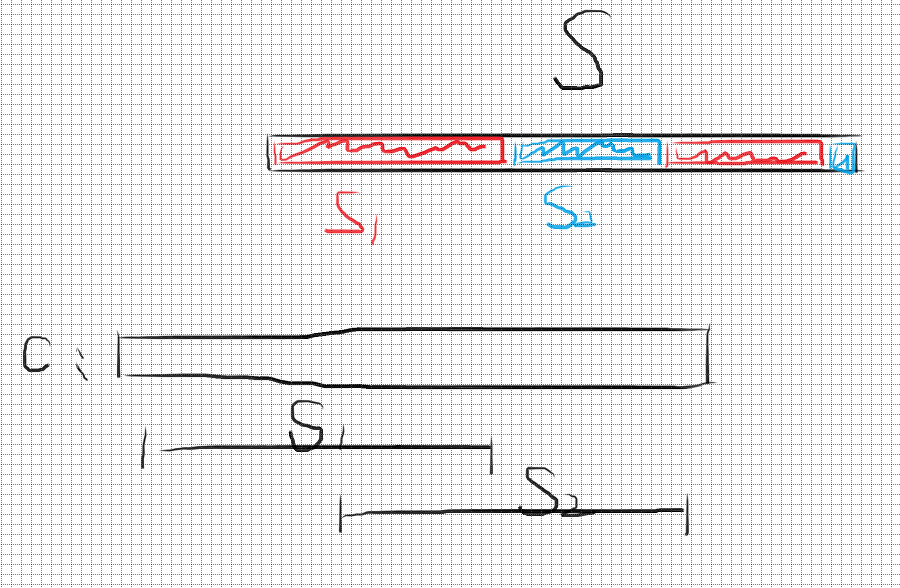
或者,从 \(\sf XYX\) 的角度:
原因在于,一个字符集能被操作的本质是,在它的最小被覆盖区间内,它自己的浓度大于等于 \(k\). 如果两种字符集分别能被操作,且彼此有交的话,一个吞掉另一个后,浓度只会增大。浓度增大后,就更能被操作了,这个不难理解。—— \(\sf XYX\)
至于如何实现?我们使用 \(\tt rnk\) 储存所有字符按照左端点排序后的结果,进行第四个转移的时候直接枚举前半部分即可。
统计答案时,对于一种字符 \(\tt x\),如果除去它的所有字符都可以被操作,那么它就是可到达的。
总时间复杂度为 \(\mathcal O(|\Sigma|2^{|\Sigma|})\).
叁、参考代码 ¶
#include<cstdio>
#include<vector>
#include<cstring>
#include<algorithm>
using namespace std;
// #define NDEBUG
#include<cassert>
namespace Elaina{
#define rep(i, l, r) for(int i=(l), i##_end_=(r); i<=i##_end_; ++i)
#define drep(i, l, r) for(int i=(l), i##_end_=(r); i>=i##_end_; --i)
#define fi first
#define se second
#define mp(a, b) make_pair(a, b)
#define Endl putchar('\n')
#define mmset(a, b) memset(a, b, sizeof a)
// #define int long long
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int, int> pii;
typedef pair<ll, ll> pll;
template<class T>inline T fab(T x){ return x<0? -x: x; }
template<class T>inline void getmin(T& x, const T rhs){ x=min(x, rhs); }
template<class T>inline void getmax(T& x, const T rhs){ x=max(x, rhs); }
template<class T>inline T readin(T x){
x=0; int f=0; char c;
while((c=getchar())<'0' || '9'<c) if(c=='-') f=1;
for(x=(c^48); '0'<=(c=getchar()) && c<='9'; x=(x<<1)+(x<<3)+(c^48));
return f? -x: x;
}
template<class T>inline void writc(T x, char s='\n'){
static int fwri_sta[1005], fwri_ed=0;
if(x<0) putchar('-'), x=-x;
do fwri_sta[++fwri_ed]=x%10, x/=10; while(x);
while(putchar(fwri_sta[fwri_ed--]^48), fwri_ed);
putchar(s);
}
}
using namespace Elaina;
const int maxn=5000;
const int maxs=1<<20;
const int sigma=20;
bool dp[maxs+5];
int l[maxs+5], r[maxs+5], cnt[maxs+5];
int id[200], refl[20], timer=-1; // pay attention to the initial value
int rnk[20];
char s[maxn+5];
int c[maxn+5];
int n, a, b, U;
/** @brief solve @p id[],refl[] and initialize @p rnk[] */
inline void init(){
for(int i='a'; i<='z'; ++i){
if(i!='t' && i!='r' && i!='y' && i!='g' && i!='u' && i!='b'){
id[i]=++timer;
refl[timer]=i;
rnk[timer]=timer;
}
}
}
inline void input(){
n=readin(1), a=readin(1), b=readin(1);
scanf("%s", s);
for(int i=0; i<n; ++i) c[i]=id[s[i]];
}
/** @brief solve @p l[],r[],cnt[] */
inline int cmp(int x, int y){
return l[1<<x]<l[1<<y];
}
#define lowbit(i) ((i)&(-(i)))
inline void statistics(){
memset(l, 0x3f, sizeof l);
for(int i=0; i<n; ++i){
l[1<<c[i]]=min(l[1<<c[i]], i);
r[1<<c[i]]=i;
++cnt[1<<c[i]];
U|=(1<<c[i]);
}
// sort @p rnk[] by the left endpos
// so that we can enumerate this array to achieve a result in which we enumerate left-more char first
sort(rnk, rnk+sigma, cmp);
for(int i=0; i<=U; ++i) if((i&U)==i && i!=lowbit(i)){
int low=lowbit(i);
l[i]=min(l[i^low], l[low]);
r[i]=max(r[i^low], r[low]);
cnt[i]=cnt[i^low]+cnt[low];
}
}
inline void getdp(){
dp[0]=1;
for(int i=1; i<=U; ++i) if((i&U)==i){
if(a*(r[i]-l[i]+1)<=b*cnt[i]){
// only one char
if(i==lowbit(i)) dp[i]=1;
else{
for(int j=0; j<sigma; ++j) if((i>>j)&1)
dp[i]|=dp[i^(1<<j)];
}
}
if(i!=lowbit(i)){
int S=0;
for(int j=0; j<sigma; ++j){
S=(S|(1<<rnk[j]))&i;
if(S && S!=i) dp[i]|=dp[S]&dp[i^S];
}
}
}
}
inline void printans(){
int ans=0;
for(int i=0; i<sigma; ++i) if(dp[U^(1<<i)])
++ans;
printf("%d", ans);
for(int i=0; i<sigma; ++i) if(dp[U^(1<<i)])
printf(" %c", refl[i]);
Endl;
}
signed main(){
init();
input();
statistics();
getdp();
printans();
return 0;
}
肆、关键的地方 ¶
一个字符集能操作时,我们并不关系它到底会被操作成什么样子,我们只需要知道它可以被操作,至于它该怎么操作,就看我们后面需要什么而自己确定了。

