[Nowcoder11244B]对序逆

[Nowcoder11244B]对序逆

壹、题目描述 ¶

定义 \(a\) 序列两位置 \(i,j\) 是逆序对的条件是 \(i<j\) 且 \(a_i>a_j\).

小 \(\mathcal O\) 喜欢魔改各种各样的排序，现在他乱搞出一种 \(\mathcal O(n^2)\) 求逆序对的新方法：

function SELECTION SORT(a)
	for i = 1 -> n-1 do
		for j = i+1 -> n do
			if a[i]>a[j] then
				swap(a[i], a[j])
				tot++
			end if
		end for
	end for
end function

小 \(\mathcal O\) 保证 \(a_i\) 是整数且 \(a_i\in[1,m]\). 他想知道这 \(m^n\) 种情况中有几种情况求出来的逆序对是正确的。

贰、题解 ¶

Part#1 Lemma

考察这个函数的性质，当 \(i\) 位置与 \(j\) 位置交换时，一定有 \(a_i\) 为 \(a_k(k\in [i,j-1])\) 中的最小数字，且 \(a_i>a_j\).

若 \([i+1,j-1]\) 中没有数字与 \(a_i\) 相同，那么将 \(a_j\) 换到 \(i\) 位置上，逆序对个数只会减少一对（这一对就是 \((a_i,a_j)\)）并没有少算，具体而言，由于 \(a_k(k\in [i+1,j-1])>a_i\)，将 \(a_i\) 换到 \(j\) 位置上和将 \(a_j\) 换到 \(i\) 位置上，减少的逆序对和增加的逆序对数量相等，相互抵消，最后剩下的就只有 \((a_i,a_j)\) 这一对没了。

但是，若 \(\exists t\in [i+1,j-1]\;\text{s.t.}\;a_t=a_i\)，那么所有 \((a_t,a_j)\) 的逆序对都在这一次交换中消失了，换而言之，它少算了。

那么，我们可以归纳出一个序列不满足条件时到底发生了什么：

\[\exists i<j<k,a_i=a_j>a_k \]

FAQ

若 \(a_k\) 在之前就被换到前面去了呢？

考虑设 \(a_k\) 与 \(a_p\) 发生交换，那么，一定有 \(p<i\)（不然我们就先换的 \(a_i\) 和 \(a_p\) 了），由于 "当 \(i\) 位置与 \(j\) 位置交换时，一定有 \(a_i\) 为 \(a_k(k\in [i,j-1])\) 中的最小数字，且 \(a_i>a_j\)"，那么，一定有 \(a_p\le a_i\)，下面分两种情况讨论：

• 当 \(a_p<a_i\) 时，换过来的数依然满足 \(a_i=a_j>a_k\)，对于扭转局面没有任何作用；
• 当 \(a_p=a_i\) 时，令 \(i'=p,j'=i(\text{or}\;j),k'=k\)，那么依然是 \(a_{i'}=a_{j'}>a_{k'}\)，发现这不是还是原来的局面？

所以，无论如何，该自闭的还是得自闭。

我们只需要算出不存在这样情况的方案数就可以了。然后我走到这一步就走不动了 \(\rm qwq\).

接下来，有两种方法计算最终的方案数。

Part#2 Calculate

Method#1 Dynamic Programming(DP)

由于和 [ARC122E]Increasing LCMs 同时写的题解，感触很深，两个题都面对同一局面 —— 填前面的格子有后效性，那么，就反过来，先填后面的。

在这道题中，我们相当于在 \(n\) 个格子中填数，且必须满足，若某个数出现了两次，那么从它第二次出现的位置开始，后面的位置填的数都不能比他小，由于这样有后效性，我们考虑反过来：若面对一个局面，剩下 \(n\) 个格子，最大能填 \(m\)，那么，如果我们想要将 \(m\) 填进去，只有采取下面的方法：

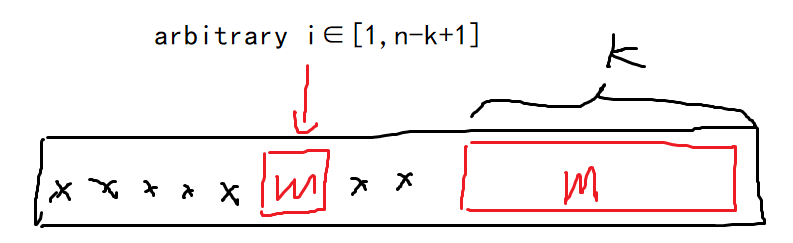
而对于剩下的位置，我们填进去的 \(m\) 对他们是没有影响的，所以，设当前的合法方案数为 \(f_{n,m}\)，那么就有

\[f_{n,m}=f_{n, m-1}+\sum_{i=1}^{n}f_{n-i,m-1}\times(n-i+1) \\ \]

对于 \(f_{n,m-1}\)，是当我们没有填 \(m\) 时的方案，这个式子复杂度为 \(\mathcal O(n^2\times n)\).

考虑对这个式子进行前缀和优化，具体地，有

\[f_{n,m}=f_{n, m-1}+\sum_{i=1}^{n}f_{n-i,m-1}\times(n-i+1) \\ \Leftrightarrow f_{n,m}=f_{n, m-1}+\sum_{i=0}^{n-1}f_{i,m-1}\times(i+1) \\ g_{n,m}\overset\Delta=\sum_{i=0}^{n-1}f_{i,m}\times(i+1)\Rightarrow g_{n,m}=g_{n-1,m}+f_{n-1,m}\times n \\ \Rightarrow f_{n,m}=f_{n,m-1}+g_{n,m-1},f_{0,m}=1 \]

就可以做到 \(\mathcal O(n^2)\) 了。

*Extra version —— Method#2 Ordinary Generating Function(OGF)

曾经，有一群神仙做过这样一道题：

染色问题-2021-03-16

时空限制：\(\rm 2s,512MB\).

我们的主人公 \(\sf yyb\) 同学最近沉迷于一款沙雕游戏无法自拔。简而言之，这款游戏的主要目的就是对摆在玩家面前的一排初始无色的格子进行染色，每次染色可以将连续一段格子染成一种之前没有出现过的颜色，要求在所有操作后 每一个格子都被染了至少一次色（重复染色会使前一次染的颜色被覆盖）。

不过神仙就是神仙，由于具有常人所不能及的强大实力，\(\sf yyb\) 在遇到新事物时总能多一份常人所不能及的深度思考。他发现在这个游戏会在开始时给出两个参数 \(n,m\)，分别表示排成一排的格子数量以及玩家可以染色的操作次数。我们不妨将这一排格子从左至右依次标号为 \(1\sim n\). 对于一次染色，玩家可以选择这一排格子中的连续一段染上一种之前没有出现过的颜色，不妨将设第 \(i\) 次染色时染成的颜色的编号为 \(i\)，初始时每个格子的颜色编号都为 \(0\)，那么对于第 \(i\) 次操作，玩家可以选择两个参数 \(l,r\) 满足 \(1\le l\le r\le n\)，并将所有满足 \(l\le j\le r\) 的 \(j\) 号格子的颜色编号改为 \(i\). 最终的游戏目标就是使得每个格子上的颜色编号都大于 \(0\). 神仙 \(\sf yyb\) 想考考你有多少种方案可以达成游戏目标，但是他觉得这太简单了，于是他打算考考你，最终达成游戏目标的不同颜色序列有多少种。由于答案可能很大，所以神仙 \(\sf yyb\) 只需要你告诉他答案对 \(998244353\) 取模后的结果就行了。

简而言之：有一个长度为 \(n\) 的序列，用 \(m\) 种颜色依次染色，每次染色的范围是一个非空区间，范围内的所有格子都会变成当前颜色（无论是否被某种颜色染色过）。

现在神仙 \(\sf yyb\) 想问你，如果要让序列的每个格子都被染过色，最终的局面有多少种不同的情况？——最终局面不同，当且仅当存在一个格子，它在两个局面中的颜色不同。

版权声明：本文为CSDN博主「OneInDark」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。

居然有四层引用！现在开始回溯吧.

最大数据点限制：满足 \(n,m\le 10^6\).

现在，这群神仙一次又一次 \(\rm AK\) 比赛，并且嘲笑其他的弱小选手。

想要解决这道题？\(\sf OneInDark\) 在这里说得已经十分明了了，就不赘述了。

但是，\(\sf closestool\) 有一种惊人的暴力推柿子的方法！在他的集训队论文里面。

叁、参考代码 ¶

这是 \(\mathcal O(n^2)\) 的暴力递推。

#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<ctime>
using namespace std;

// #define NDEBUG
#include<cassert>

namespace Elaina{
    #define rep(i, l, r) for(int i=(l), i##_end_=(r); i<=i##_end_; ++i)
    #define drep(i, l, r) for(int i=(l), i##_end_=(r); i>=i##_end_; --i)
    #define fi first
    #define se second
    #define mp(a, b) make_pair(a, b)
    #define Endl putchar('\n')
    #define mmset(a, b) memset(a, b, sizeof a)
    // #define int long long
    typedef long long ll;
    typedef pair<int, int> pii;
    typedef pair<ll, ll> pll;
    template<class T>inline T fab(T x){ return x<0? -x: x; }
    template<class T>inline void getmin(T& x, const T rhs){ x=min(x, rhs); }
    template<class T>inline void getmax(T& x, const T rhs){ x=max(x, rhs); }
    template<class T>inline T readin(T x){
        x=0; int f=0; char c;
        while((c=getchar())<'0' || '9'<c) if(c=='-') f=1;
        for(x=(c^48); '0'<=(c=getchar()) && c<='9'; x=(x<<1)+(x<<3)+(c^48));
        return f? -x: x;
    }
    template<class T>inline void writc(T x, char s='\n'){
        static int fwri_sta[1005], fwri_ed=0;
        if(x<0) putchar('-'), x=-x;
        do fwri_sta[++fwri_ed]=x%10, x/=10; while(x);
        while(putchar(fwri_sta[fwri_ed--]^48), fwri_ed);
        putchar(s);
    }
}
using namespace Elaina;

const int mod=998244353;
const int maxn=1e4;

int n, m, ans;

int f[maxn+5], g[maxn+5];

signed main(){
    n=readin(1), m=readin(1);
    f[0]=1;
    rep(i, 1, n) f[i]=1, g[i]=g[i-1]+f[i-1]*i;
    rep(j, 2, m){
        rep(i, 1, n){
            f[i]=(f[i]+g[i])%mod;
            g[i]=(g[i-1]+1ll*f[i-1]*i%mod)%mod;
        }
    }
    writc(f[n]);
    return 0;
}

肆、关键的地方 ¶

挖掘性质是其一，另外就是 “填前面的格子有后效性，那么，就反过来，先填后面的。”，其实就是 [ARC122E]Increasing LCMs 的关键。