[HDU6800]Play osu! on Your Tablet
壹、题目描述
贰、题解
定义 \(\text{dis}(x,y)\) 表示 \(x,y\) 的曼哈顿距离,定义 \(\text{dis}(i_1,i_2,i_3,...,i_t)\) 表示 \(\sum_{k=1}^{k<t}\text{dis}(i_k,i_{k+1})\).
定义 \(f_{i,j}\) 表示考虑了前 \(i\) 个数字,其中一个序列的结尾在 \(j\) 的最小曼哈顿距离,发现对于 \(j<i-1\) 的情况,肯定是我们没有维护的序列之前以 \(i-1\) 结尾,维护的序列就是 \(j\) 结尾了,同时我们最后选择的数字归于没有维护的这一个数列(即以 \(i-1\) 结尾的这一个数列),那么我们可以直接从 \(i-1\) 转移
对于 \(j=i-1\) 的情形,我们无法转移,因为在 \(f_{i-1}\) 中的前驱状态不清楚,我们知道前驱状态中我们维护的序列结尾是 \(i-1\),但是没有维护的序列呢?所以这个时候我们就得枚举这个序列结束的位置,从 \(f_{i-1,k}\) 转移(注意此处的 \(f_{i-1,k}\) 和 \(f_i\) 维护的序列是不一样的,交换过后的)
也就是
我们将 \(f_{i-1,k}\) 继续迭代展开:
如果我们将 \(f_{i-2,k}\) 继续展开,同样也会得到一个类似的结果,然后我们发现,最后一定是这样的一个结果:
这个转移的本质是什么?考虑下面这一张图:
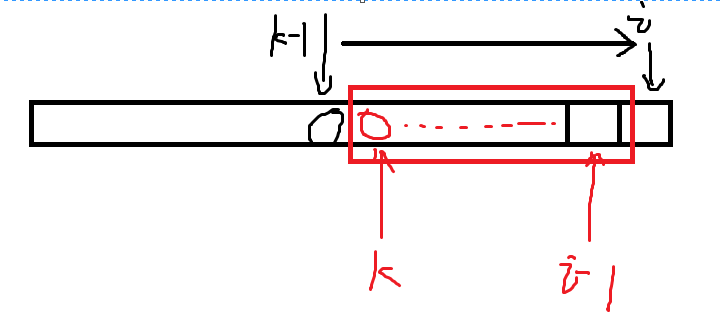
实际上我们就是枚举另一个序列在结尾部分的长度,然后进行转移。
同时,发现只涉及 \(f_{i,i-1}\) 之间的转移,我们考虑单独做,记 \(g_i=f_{i,i-1}\),那么有
考虑记 \(s_i=\text{dis}(1,2,3,...,i)\),那么
我们可以考虑使用 \(\tt CDQ\) 分治,考虑左区间对于右区间的贡献,但是由于 \(\text{dis}(j-1,i)\) 带绝对值,需要考虑将点 \(j-1\) 与点 \(i\) 的相对位置分四种情况讨论,每种情况将和 \(j\) 有关的放在一起,将和 \(i\) 有关的放在一起,最后就变成了一个二维数点的类似的问题,总复杂度 \(\mathcal O(n\log^2 n)\).
但是还有一部分 \(f_{i,j}(j<i-1)\) 的部分怎么办?我们同样将转移式子展开,最后可以得到
所以最后加一个循环即可。
叁、参考代码
\(\color{red}{\text{Talk is s**t, show you the code.}}\)
#include<cstdio>
#include<algorithm>
using namespace std;
typedef long long ll;
template<class T>inline T fab(const T x){return x<0? -x: x;}
template<class T>inline T readin(T x){
x=0; int f=0; char c;
while((c=getchar())<'0' || '9'<c) if(c=='-') f=1;
for(x=(c^48); '0'<=(c=getchar()) && c<='9'; x=(x<<1)+(x<<3)+(c^48));
return f? -x: x;
}
const int maxn=1e5;
const ll inf=1ll<<60;
int n, T;
ll s[maxn+5];
struct point{
int x, y, id;
point(){}
point(const int X, const int Y): x(X), y(Y), id(0){}
inline int operator <(const point rhs) const{
return x<rhs.x;
}
}p[maxn+5];
inline ll dis(const int i, const int j){
return fab(p[i].x-p[j].x)+fab(p[i].y-p[j].y);
}
inline void input(){
n=readin(1);
for(int i=1; i<=n; ++i){
p[i].x=readin(1), p[i].y=readin(1);
if(i>1) s[i]=s[i-1]+dis(i-1, i);
}
}
inline int lowbit(const int i){return i&(-i);}
struct BIT1{
ll c[maxn+5]; int siz;
inline void clear(const int up){
siz=up;
for(int i=0; i<=siz; ++i) c[i]=inf;
}
inline void add(int i, const ll val){
for(; i<=siz; i+=lowbit(i))
c[i]=min(c[i], val);
}
inline ll query(int i){
ll ret=inf;
for(; i; i-=lowbit(i))
ret=min(ret, c[i]);
return ret;
}
}upp;
struct BIT2{
ll c[maxn+5]; int siz;
inline void clear(const int up){
siz=up;
for(int i=0; i<=siz; ++i) c[i]=inf;
}
inline void add(int i, const ll val){
for(; i; i-=lowbit(i))
c[i]=min(c[i], val);
}
inline ll query(int i){
ll ret=inf;
for(; i<=siz; i+=lowbit(i))
ret=min(c[i], ret);
return ret;
}
}downp;
// assisted array
point t[maxn+5];
ll g[maxn+5];
int hashy[maxn+5];
struct node{
int y, id;
node(){}
node(const int Y, const int I): y(Y), id(I){}
inline int operator <(const node rhs) const{
return y<rhs.y;
}
}ty[maxn+5];
inline int cmp1(const point a, const point b){
if(a.x==b.x) return a.id<b.id;
return a.x<b.x;
}
inline int cmp2(const point a, const point b){
if(a.x==b.x) return a.id<b.id;
return a.x>b.x;
}
void solve(const int l, const int r){
if(l==r) return;
int mid=(l+r)>>1;
solve(l, mid);
for(int i=l-1; i<=r; ++i)
ty[i]=node(p[i].y, i);
sort(ty+l-1, ty+r+1);
int has_num=0, pre=-1;
for(int i=l-1; i<=r; ++i){
if(ty[i].y!=pre) ++has_num, pre=ty[i].y;
hashy[ty[i].id]=has_num;
}
// copy the array
for(int i=l; i<=mid; ++i)
t[i]=p[i-1], t[i].id=i;
for(int i=mid+1; i<=r; ++i)
t[i]=p[i], t[i].id=i;
sort(t+l, t+r+1, cmp1);
upp.clear(has_num), downp.clear(has_num);
for(int i=l; i<=r; ++i){
if(t[i].id<=mid){
// if this point is under
upp.add(hashy[t[i].id-1], g[t[i].id]-s[t[i].id]-t[i].x-t[i].y);
// if this point is over
downp.add(hashy[t[i].id-1], g[t[i].id]-s[t[i].id]-t[i].x+t[i].y);
}
else{
g[t[i].id]=
min(g[t[i].id],
min(upp.query(hashy[t[i].id])+s[t[i].id-1]+t[i].x+t[i].y,
downp.query(hashy[t[i].id])+s[t[i].id-1]+t[i].x-t[i].y
));
}
}
upp.clear(has_num), downp.clear(has_num);
sort(t+l, t+r+1, cmp2);
for(int i=l; i<=r; ++i){
if(t[i].id<=mid){
upp.add(hashy[t[i].id-1], g[t[i].id]-s[t[i].id]+t[i].x-t[i].y);
downp.add(hashy[t[i].id-1], g[t[i].id]-s[t[i].id]+t[i].x+t[i].y);
}
else{
g[t[i].id]=
min(g[t[i].id],
min(upp.query(hashy[t[i].id])+s[t[i].id-1]-t[i].x+t[i].y,
downp.query(hashy[t[i].id])+s[t[i].id-1]-t[i].x-t[i].y
));
}
}
solve(mid+1, r);
}
signed main(){
T=readin(1);
while(T--){
input();
if(n<=2){
printf("0\n");
continue;
}
g[1]=0;
for(int i=2; i<=n; ++i) g[i]=s[i-1];
solve(2, n);
ll ans=inf;
for(int j=1; j<=n; ++j)
ans=min(ans, g[j]+s[n]-s[j]);
printf("%lld\n", ans);
}
return 0;
}
卡住原因:
- 某些地方将 \(\min\) 打成 \(\max\);
- 对于 \([l,r]\) 的数组的复制,对于 \([l,mid]\) 和 \([mid+1,r]\) 的部分,拷贝需要使用不同的点坐标;
- 需要将 \(y\) 哈希;
- 树状数组的 \(\pm\) 要判断清楚;
肆、用到の小 \(\tt trick\)
写 \(DP\) 式子的时候要深入地考虑,分析其本质,最后可能会发现一些意想不到的惊喜。
对于带绝对值的东西,由于非线性不好分析,可以考虑将情况分开,将绝对值去掉之后用更简单的方案,但是这样做一般会将问题转化为一个类似二维数点的问题,这个时候就需要各种数据结构进行维护了。

