[组合计数题单]整除!整除!
真就举觞白眼望青天了呗,什么都不知道......
壹、题目
给出 \(n\) 个正整数 \(a_i\),要求分别选出 \(n\) 个正整数 \(b_i\) 和 \(d_i\),并且要满足 \(b_i\mid a_i\),且 \(d_i\mid b_i\),求多少种选法满足 \(\prod_{i=1}^nd_i^2>\prod_{i=1}^nb_i\).
贰、题解
题解妙啊~~
注意到 \(\prod_{i=1}^nd_i^2>\prod_{i=1}^nb_i\) 与 \(\prod_{i=1}^nd_i^2<\prod_{i=1}^nb_i\) 是一一对应的,即如果令 \(d_i={b_i\over d_i}\),那么大于小于号就反过来了。
唯一比较特别的就是 \(\prod_{i=1}^nd_i^2=\prod_{i=1}^nb_i\) 的情况,如果我们从所有方案种去除这种情况,那么我们要求的选法数量就是剩下方案数量的 \(1\over 2\) 了。
从质因子的角度考虑,满足 \(\prod_{i=1}^nd_i^2=\prod_{i=1}^nb_i\) 即 \(d_i\) 中每个质因子恰好是所有 \(b_i\) 这个质因子的 \(\frac{1}{2}\),而由于每个质因子是独立的,考虑每个质因子单独做一遍背包,定义 \(f_{i,j}\) 为前 \(i\) 个数,选了质因子的数量 - 没选的质因子的数量的值为 \(j\) 的情况的方案数,具体说明一下,有这样一种情况:
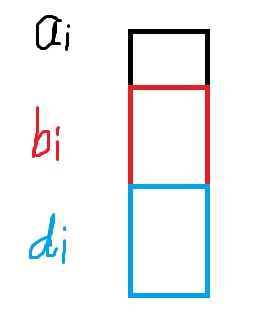
对于一个质因子,\(a_i\) 的数量是最多的,其次是 \(b_i\),最后是 \(d_i\),如果我们最终要让 \(\prod b_i=\prod d_i^2\),也就是要让每个质因子,\(b_i\) 是 \(d_i\) 的两倍,即对于所有 \(i\),图中红色框框与蓝色框框的数值之和相同,定义这个状态之后,做一个背包就可以了,我们最后要的就是 \(f_{n,0}\).
如果要去掉负数情况,可以考虑使用 \(\tt map\),或者整体平移。
叁、用到の小 \(\tt trick\)
对于一个数 \(a|b\),可以考虑 \(a\) 与 \(\frac{b}{a}\) 之间的关系,例如 \(a,{b\over a}\) 与 \(\sqrt b\) 之间的大小关系是反过来的,没见过 。
整除、累乘之类的东西,可以尝试往质因子个数方向,而这个 "个数" 通常和背包之类的东西挂钩。


