[HDU6848]Expectation
题目
补一个数据范围:
| 测试点编号 | $n\le $ |
|---|---|
| 1 | \(1\) |
| 2 | \(2\) |
| 3 | \(5\) |
| 4 | \(10\) |
| 5 | \(50\) |
| 6 | \(100\) |
| 7 | \(300\) |
| 8 | \(500\) |
| 9 | \(1000\) |
| 10 | \(3000\) |
题解
呐,话说,测试点 1,2,3 不是可以手算吗?
小球进洞模型 虽然我没见过就是了
其实这道题和期望没什么关系,设 \(S\) 为所有方案的移动总距离,显然最后要求的就是
我们只要求出 \(S\),最后乘上 \(n!2^n\) 的逆就可以了.
现在难点在于求 \(S\),这个时候各种方法就大放光彩了......
算法零
人工组合数计算 \(n=1,2,5\) 时 \(2n\) 条边分别被经过好多次,然后直接打表输出,时间复杂度 \(\mathcal O(1)\),期望得分 \(30pts\) 这不是爆踩 std ?
你已经为你的代码做了太多事
算法一
所谓算法竞赛,就是拼谁暴力打得好,有 \(n!2^n\) 个方案?那我全部枚举出来就是了...
时间复杂度 \(\mathcal O(n!2^n)\),期望得分 \(30pts\). 这也是我上交的代码
为什么题解写这个算法只有 \(20pts\)...... 手算都比这高
算法二
在算法一的基础上,将暴力改成状压,定义 \(f[i][s1][s2]\) 表示现在选择第 \(i\) 个球,可选的球状态为 \(s1\),可选的洞状态为 \(s2\).
不难发现状态有 \(n\times 2^n\times 2^{n+1}\) 个,时间复杂度也就是 \(\mathcal O(2^n\times 2^{n+1}\times n)=\mathcal O(2^{2n+1}\times n)\) 了 或许有更好的写法,时间复杂度更低?
期望得分 \(40pts\).
算法三和四的正规版本来源于知名博主 C202044zxy,这里是传送门.
下面是个人 yy,可能会有细节问题,意会即可......
算法三
记第 \(i\) 个洞左边的球编号为 \(i\),往下挖掘性质:发现将 \([l,r]\) 的洞填满,要用到的球只有可能在 \([l,r+1]\),洞有 \(r-l+1\) 个,球有 \(r-l+2\) 个,必定会剩下一个球 \(k\),这个 \(k\) 相当于将整个区间 \([l,r]\) 分成两个部分:\([l,k-1]\) 与 \([k+1,r]\) 两个区间内部自行解决.
我们可以考虑区间 \(DP\),状态显然,定义 \(f[l][r]\) 表示将 \([l,r]\) 的行星撞完的所有方案移动距离和,考虑转移,我们就枚举剩下的球是哪个
最后,有 \(S=f[1][n]\),同样还要乘上逆元.
时间复杂度 \(\mathcal O(n^3)\),期望得分 \(80pts\).
算法四
对于算法三,我们展开转移方程之后发现可以使用前缀和优化,将转移降至 \(\mathcal O(1)\),时间复杂度为 \(\mathcal O(n^2)\),期望得分 \(100pts\).
算法五
和算法三、四利用的性质不一样,我们得挖掘另外的性质.
我们考虑有 \(n\) 个球的情况,这个时候一共有 \(2n+1\) 个点,\(2n\) 个区间,我们不妨画一个简易的图出来:
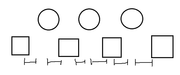
这个图中,\(n=3\).
其中圆的是球,方形是洞,下面的线段表示的是区间,我们随便选一个球出来,让它随便进一个洞,就变成这样:
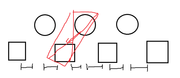
一个球和一个洞抵消掉了,而这个抵消操作,实际上就是选择一条边,将这条边连接的球和洞抵消,上述情况中我们选择的是第 \(3\) 条边.
这个时候,我们的场面上还剩下 \(2\) 个球,\(3\) 个洞,这是一个有 \(4\) 条边的子局面,为什么边变少了,因为这三条边变成同一条了:
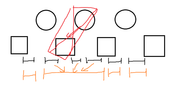
我们发现,原来的第 \(2,3,4\) 条边全部变成子局面中的第 \(2\) 条边.
而这个子结构中,如果我们要统计原来的第 \(3\) 条边被经过了多少次,实际上就是统计在两个球下的第 \(2\) 条边被经过了多少次,不妨设 \(f[i][j]\) 为有 \(i\) 个球时,第 \(j\) 条边被走了多少次,那么上述就是
我们考虑完善这个转移方程,如果我们选择的不是第 \(3\) 条边,而是其他的边,比如说第 \(2\) 条?我们发现这个时候第三条边变成子状态的第一条边.
我们再尝试一下,如果选择第 \(4\) 条边,第三条边在子状态中还是第三条边,而选择第 \(5,6\) 条边效果是一样的.
我们完善这个方程,有
总结上述规律:对于 \(i\) 个球下的第 \(j\) 条边:
- 选择 \([1,j-1]\) 中的某条边,\((i,j)\rightarrow(i-1,j-2)\);
- 选择 \(j\),\((i,j)\rightarrow (i-1,j-1)\);
- 选择 \([j+1,2i]\),\((i,j)\rightarrow (i-1,j)\);
转移方程为
初始化 \(f_{1,1}=f_{1,2}=1\),这个类似于预处理,复杂度 \(\mathcal O(n^2)\),然后,我们再来个 \(\mathcal O(n)\) 线性求 \(S\) 即可.
但是,这样会
为什么?我们所谓的“选择”,统计的是什么?上面的转移统计的全部都是在先合并其他球和边的方案中,经过 \(j\) 的情况,而我们并没有统计首先就选择 \(j\) 的方案,所以需要加上 \((i-1)2^{i-1}\).
所以转移方程就是
时间复杂度 \(\mathcal O(n^2+n)\).
\(p.s.\) 这道题在 \(HDU\) 上好像还有一个 \(T\le 2000\),对于算法三、四似乎过不去...
#include<iostream>
using namespace std;
namespace IO{
#define rep(i,__l,__r) for(signed i=(__l),i##_end_=(__r);i<=i##_end_;++i)
#define fep(i,__l,__r) for(signed i=(__l),i##_end_=(__r);i>=i##_end_;--i)
#define low_rep(i,__l,__r) for(signed i=(__l),i##_end_=(__r);i<i##_end_;++i)
#define upp_fep(i,__l,__r) for(signed i=(__l),i##_end_=(__r);i>=i##_end_;--i)
#define erep(i,u) for(signed i=tail[u],v=e[i].to;i;i=e[i].nxt,v=e[i].to)
#define writc(a,b) fwrit(a),putchar(b)
#define mp(a,b) make_pair(a,b)
#define fi first
#define se second
typedef long long ll;
// typedef pair<int,int> pii;
typedef unsigned long long ull;
typedef unsigned uint;
#define Endl putchar('\n')
// #define int long long
// #define int unsigned
// #define int unsigned long long
#define cg (c=getchar())
template<class T>inline void readin(T& x){
char c;bool f=0;
while(cg<'0'||'9'<c)f|=(c=='-');
for(x=(c^48);'0'<=cg&&c<='9';x=(x<<1)+(x<<3)+(c^48));
if(f)x=-x;
}
template<class T>inline T readin(T x){
x=0;char c;bool f=0;
while(cg<'0'||'9'<c)f|=(c=='-');
for(x=(c^48);'0'<=cg&&c<='9';x=(x<<1)+(x<<3)+(c^48));
return f?-x:x;
}
template<class T>void fwrit(const T x){//just short,int and long long
if(x<0)return (void)(putchar('-'),fwrit(-x));
if(x>9)fwrit(x/10);
putchar(x%10^48);
}
#undef cg
template<class T>inline T Max(const T x,const T y){return x<y?y:x;}
template<class T>inline T Min(const T x,const T y){return x<y?x:y;}
template<class T>inline T fab(const T x){return x>0?x:-x;}
inline int gcd(const int a,const int b){return b?gcd(b,a%b):a;}
inline void getInv(int inv[],const int lim,const int MOD){
inv[0]=inv[1]=1;for(int i=2;i<=lim;++i)inv[i]=1ll*inv[MOD%i]*(MOD-MOD/i)%MOD;
}
inline ll mulMod(const ll a,const ll b,const ll mod){//long long multiplie_mod
return ((a*b-(ll)((long double)a/mod*b+1e-8)*mod)%mod+mod)%mod;
}
}
using namespace IO;
const int maxn=3000;
const int mod=998244353;
inline int inv(int a){
int n=mod-2,ret=1;
for(;n>0;n>>=1,a=1ll*a*a%mod)if(n&1)ret=1ll*ret*a%mod;
return ret;
}
int f[maxn+5][maxn*2+5];
inline void Init(){
f[1][1]=f[1][2]=1;
int tmp=1;
rep(i,2,maxn){
tmp=1ll*tmp*(i-1)%mod*2%mod;
rep(j,1,i*2)
f[i][j]=
(
0ll+/*tmp+*/f[i-1][j-1]+
1ll*f[i-1][j]*(2*i-j)%mod+
(j>=2?(1ll*(j-1)*f[i-1][j-2])%mod:0)
)
%mod;
}
}
int x[maxn*2+5],n,N;
signed main(){
// freopen("stars.in","r",stdin);
// freopen("stars.out","w",stdout);
Init();
cin>>n;N=(n<<1)+1;
// rep(i,1,n){
// rep(j,1,N){
// printf("f[%d, %d] == %d\n",i,j,f[i][j]);
// }Endl;
// }
rep(i,1,N)cin>>x[i];
int ans=0;
rep(i,1,N-1)ans=(ans+1ll*f[n][i]*(x[i+1]-x[i])%mod)%mod;
int fac=1,pow2=1;
rep(i,1,n)fac=1ll*fac*i%mod,pow2=1ll*pow2*2%mod;
cout<<1ll*ans*inv(fac)%mod*inv(pow2)%mod<<'\n';
return 0;
}


