[WC2011]最大XOR和路径
题目
题解
由于路径价值为异或和,显然一条路如果重复走就没有价值了。
我们可以考虑选取一条从 \(1\) 到 \(N\) 的简单路径,中间的路径用环进行拓展。
但是,我们从简单路径到环,中间还要经过一条路径,这条路径考虑会走几遍:首先,我们从简单路径到环会走一遍,然后我们从环再走到路径上,会走两遍,根据异或的特性,这条路径被异或两次,那么就没有贡献。
那么,我们所选取的路径价值就是:
\[W_{简单路径}\oplus W_{拓展环}
\]
但是,简单路径的价值如果没有找到最优,会不会对我们的答案造成影响呢?
考虑这样一种形式:
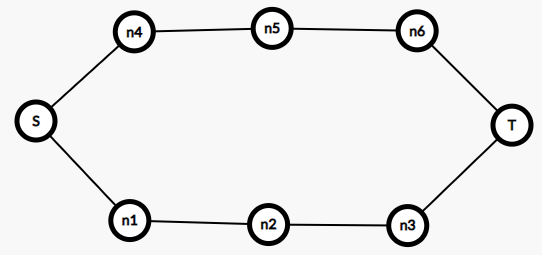
假设我们找到的任意一条简单路径是 \(S-n_1-n_2-n_3-T\),但是我们从 \(S-n_4-n_5-n_6-T\) 更优,那么,我们最后在枚举 \(W_{简单路径}\oplus W_{拓展环}\) 时,我们会遇到 \(W_{S-n_1-n_2-n_3-T}\oplus W_{环:S-n_1-n_2-n_3-T-n_6-n_5-n_4-S}\),那么,这条路径实际上就变成了 \(W_{S-n_4-n_5-n_6-T}\)。
#include<bits/stdc++.h>
using namespace std;
#define rep(i,__l,__r) for(signed i=(__l),i##_end_=(__r);i<=i##_end_;++i)
#define fep(i,__l,__r) for(signed i=(__l),i##_end_=(__r);i>=i##_end_;--i)
#define writc(a,b) fwrit(a),putchar(b)
#define mp(a,b) make_pair(a,b)
#define ft first
#define sd second
#define LL long long
#define ull unsigned long long
#define uint unsigned int
#define pii pair< int,int >
#define Endl putchar('\n')
// #define int long long
// #define int unsigned
// #define int unsigned long long
#define cg (c=getchar())
template<class T>inline void qread(T& x){
char c;bool f=0;
while(cg<'0'||'9'<c)f|=(c=='-');
for(x=(c^48);'0'<=cg&&c<='9';x=(x<<1)+(x<<3)+(c^48));
if(f)x=-x;
}
inline int qread(){
//just for int(When the code defines int long long, the function is just for long long)
int x=0;char c;bool f=0;
while(cg<'0'||'9'<c)f|=(c=='-');
for(x=(c^48);'0'<=cg&&c<='9';x=(x<<1)+(x<<3)+(c^48));
return f?-x:x;
}
#undef cg
// template<class T,class... Args>inline void qread(T& x,Args&... args){qread(x),qread(args...);}
template<class T>inline T Max(const T x,const T y){return x>y?x:y;}
template<class T>inline T Min(const T x,const T y){return x<y?x:y;}
template<class T>inline T fab(const T x){return x>0?x:-x;}
inline int gcd(const int a,const int b){return b?gcd(b,a%b):a;}
inline void getInv(int inv[],const int lim,const int MOD){
inv[0]=inv[1]=1;for(int i=2;i<=lim;++i)inv[i]=1ll*inv[MOD%i]*(MOD-MOD/i)%MOD;
}
template<class T>void fwrit(const T x){//just short,int and long long
if(x<0)return (void)(putchar('-'),fwrit(-x));
if(x>9)fwrit(x/10);
putchar(x%10^48);
}
inline LL mulMod(const LL a,const LL b,const LL mod){//long long multiplie_mod
return ((a*b-(LL)((long double)a/mod*b+1e-8)*mod)%mod+mod)%mod;
}
const int MAXN=5e4;
const int MAXM=1e5;
struct edge{
int to,nxt;
LL w;
}e[(MAXM<<1)+5];
int tail[MAXN+5],ecnt;
inline void add_edge(const int u,const int v,const LL w){
e[++ecnt]=edge{v,tail[u],w};tail[u]=ecnt;
e[++ecnt]=edge{u,tail[v],w};tail[v]=ecnt;
}
template<class T>struct Basic{
#define MAXSIZE 60
LL f[MAXSIZE+5],flg;
//flg 记录插入时是否有不能放入的数
/*
inline int high_pos(T num){
int ret=-1;
while(num>0)num>>=1,++ret;
return ret;
}
inline void insert(T num){
int t;
while(num && f[t=high_pos(num)])num^=f[t];
if(num)f[t]=num;
else flg=true;
}
*/
inline void insert(T num){
fep(i,MAXSIZE,0){
if(!(num>>i))continue;
if(!f[i]){f[i]=num;return;}
num^=f[i];
}
flg=true;
}
inline T queryMax(T ret){
fep(i,60,0)if((ret^f[i])>ret)
ret^=f[i];
return ret;
}
inline T queryMin(){
if(flg)return 0;
T ret=(1ll<<MAXSIZE);
rep(i,0,60)ret=Min(ret,f[i]);
}
};
Basic<LL>G;
int n,m;
LL ans;
bool vis[MAXN+5];
LL pw[MAXN+5];
void dfs(const int u,const LL w){
if(u==n)ans=w;
if(vis[u])return G.insert(w^pw[u]);
vis[u]=true,pw[u]=w;
for(int i=tail[u];~i;i=e[i].nxt)
dfs(e[i].to,w^e[i].w);
}
signed main(){
memset(tail,-1,sizeof tail);
// cin>>n>>m;
scanf("%d %d",&n,&m);
int u,v;LL w;
rep(i,1,m){
// cin>>u>>v>>w;
scanf("%d %d %lld",&u,&v,&w);
add_edge(u,v,w);
}
dfs(1,0);
cout<<G.queryMax(ans)<<'\n';
return 0;
}


