「题解」「CF850A」Five Dimensional Points
题目
题解
本题暴力可过,细节不必多说。
这里我主要是说明一下为什么当 \(n>11\) 时可以直接输出 \(0\) 。
首先,思考二维空间中,我们能保证最多能同时存在多少点,而还有好点存在?
答案是 \(5\) 个,为什么?
可以手画一下,二维平面内五个点构成“十”字结构。
在这种情况下,点数最多。
进行拓展——三维呢?提示:可以从二维进行拓展。
答案是 \(7\) 个,为什么?
首先,我们在三维坐标系中画出二维结论,大概是这个鸭子(注意,全都是直角)
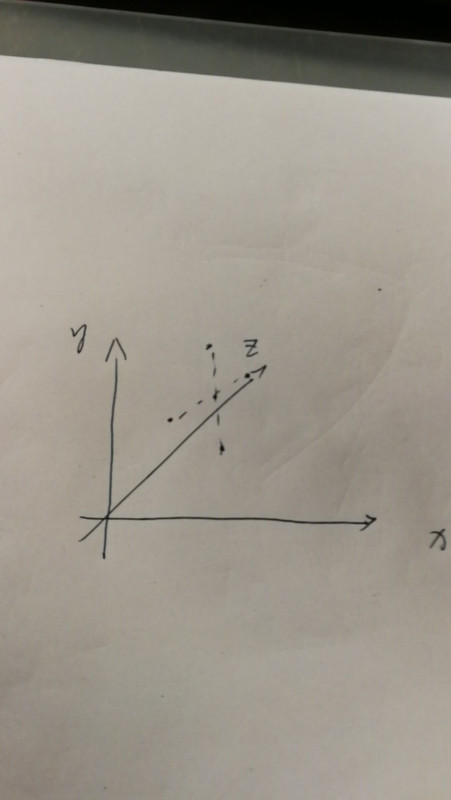
为了让点更多,我们从二维中学到了一个结构——“十”字结构,这个结构能让点最多。
推广一下——其实我们是在构造直角。
同时,还有一个结论——对于 \(A,B,C\) 三个点,如果 \(A\) 是好点,那么 \(B,C\) 一定是坏点。
为了让点数最多,我们贪心地让只让一个点成为好点,也就是只要其他的点不干扰这个点,点就可以随便加。
而加点时,只要我们遵循“十”字结构,那么点一定会是最多。
显然,在上图中,中间那个点是好点,那么我们只需要让它继续保持是好点,同时我们构造更多的直角,那么我们可以画出三维最多的图:
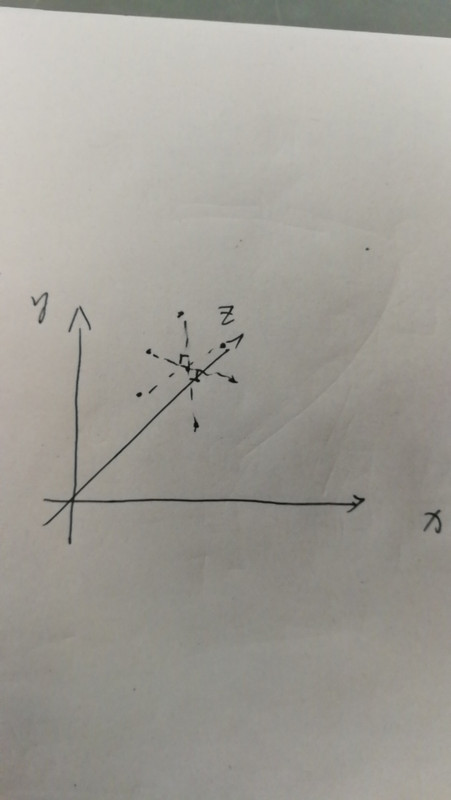
显然,这个时候有 \(7\) 个点,有点像两个“十”拼在一起,中间的轴是同一个。
至于更高维,我们画不出来了,但是可以推广。
多一维,相当于可以新增加一个“十”,那么加的点是多少?
很容易算,\(5-3=2\) ,为什么 \(-3\) ,因为我们为了保证还有一个好点,让多个“十”的中轴绑在一起,减掉轴上的 \(3\) 个点,自然而然增加了 \(2\) 个。
那么,四维最多 \(9\) 个,五维 \(11\) 个。
因而当 \(n>11\) 时,直接输出 \(0\) 即可。
代码
#include<cstdio>
#define rep(i,__l,__r) for(signed i=__l,i##_end_=__r;i<=i##_end_;++i)
#define fep(i,__l,__r) for(signed i=__l,i##_end_=__r;i>=i##_end_;--i)
#define writc(a,b) fwrit(a),putchar(b)
#define mp(a,b) make_pair(a,b)
#define ft first
#define sd second
#define LL long long
#define ull unsigned long long
#define uint unsigned int
#define pii pair< int,int >
#define Endl putchar('\n')
// #define FILEOI
// #define int long long
// #define int unsigned
#ifdef FILEOI
# define MAXBUFFERSIZE 500000
inline char fgetc(){
static char buf[MAXBUFFERSIZE+5],*p1=buf,*p2=buf;
return p1==p2&&(p2=(p1=buf)+fread(buf,1,MAXBUFFERSIZE,stdin),p1==p2)?EOF:*p1++;
}
# undef MAXBUFFERSIZE
# define cg (c=fgetc())
#else
# define cg (c=getchar())
#endif
template<class T>inline void qread(T& x){
char c;bool f=0;
while(cg<'0'||'9'<c)f|=(c=='-');
for(x=(c^48);'0'<=cg&&c<='9';x=(x<<1)+(x<<3)+(c^48));
if(f)x=-x;
}
inline int qread(){
int x=0;char c;bool f=0;
while(cg<'0'||'9'<c)f|=(c=='-');
for(x=(c^48);'0'<=cg&&c<='9';x=(x<<1)+(x<<3)+(c^48));
return f?-x:x;
}
// template<class T,class... Args>inline void qread(T& x,Args&... args){qread(x),qread(args...);}
template<class T>inline T Max(const T x,const T y){return x>y?x:y;}
template<class T>inline T Min(const T x,const T y){return x<y?x:y;}
template<class T>inline T fab(const T x){return x>0?x:-x;}
inline int gcd(const int a,const int b){return b?gcd(b,a%b):a;}
inline void getInv(int inv[],const int lim,const int MOD){
inv[0]=inv[1]=1;for(int i=2;i<=lim;++i)inv[i]=1ll*inv[MOD%i]*(MOD-MOD/i)%MOD;
}
template<class T>void fwrit(const T x){
if(x<0)return (void)(putchar('-'),fwrit(-x));
if(x>9)fwrit(x/10);
putchar(x%10^48);
}
inline LL mulMod(const LL a,const LL b,const LL mod){//long long multiplie_mod
return ((a*b-(LL)((long double)a/mod*b+1e-8)*mod)%mod+mod)%mod;
}
const int MAXN=1e3;
struct point{
int a[6];
}p[MAXN+5];
int n,tail;
int ans[MAXN+5];
bool flg;int calc;
signed main(){
#ifdef FILEOI
freopen("file.in","r",stdin);
freopen("file.out","w",stdout);
#endif
scanf("%d",&n);
rep(i,1,n)rep(j,1,5)p[i].a[j]=qread();
if(n>11)return puts("0"),0;
rep(i,1,n){
flg=false;
rep(j,1,n)if(i^j){
rep(k,1,n)if(k^i && k^j){
calc=0;
rep(t,1,5)calc+=(p[i].a[t]-p[j].a[t])*(p[i].a[t]-p[k].a[t]);
if(calc>0){flg=true;break;}
}
if(flg)break;
}
if(!flg)ans[++tail]=i;
}
writc(tail,'\n');
rep(i,1,tail)writc(ans[i],' ');
Endl;
return 0;
}

