位运算-位1的个数
leetcode 191. 编写一个函数，输入是一个无符号整数（以二进制串的形式），返回其二进制表达式中数字位数为 '1' 的个数。即 汉明重量
示例 1：
输入：00000000000000000000000000001011
输出：3
解释：输入的二进制串 00000000000000000000000000001011 中，共有三位为 '1'。
示例 2：
输入：00000000000000000000000010000000
输出：1
解释：输入的二进制串 00000000000000000000000010000000 中，共有一位为 '1'。
来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/number-of-1-bits
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。
循环与位移动
- 思路：判断二进制数的每一位是否为1。将待检测位和工具1进行 位与 运算，值为1，计数器+1，否则不变。重复该过程至将工具1移至最高位（32）。
- 代码：
def hammingWeight(self, n: int) -> int:
# 1. 若n很小的话没必要循环32次
res = sum(1 for i in range(32) if n & (1<<i))
return ret
1<<i 理解为：
1 << 1 --> 10 (2)
1 << 2 --> 100 (4)
# 若 n 为 0...01011
# i = 0
n & (1<<i) -->
01011
& 00001
= 00001(对应位同时为1时，&结果才为1)
# i = 1
n & (1<<i) -->
01011
& 00010
= 00010 (!=0, count+=1)
# 以此类推至i=32
- 缺点：对任意的整数，都要执行32次移位和与操作，如果整数比较小，其余位的操作就是冗余的。
n & (n-1)
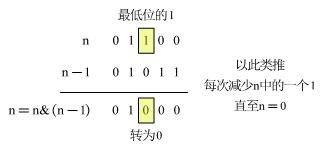
- 思路：将整数n的最低位的1变为0，循环至n=0，循环的次数即n中包含1的数量。
- 如何实现最低为1转为0： n & (n-1)
def hammingWeight(self, n: int) -> int:
# 2. 每次对n进行-1，将(n-1)与n做与操作，若 n&(n-1) != 0， 则说明还包含1
ret = 0
while n:
ret += 1
# 每次 & 相当于给n减少了一个1
n &= (n-1)
return ret
- 以上两种方法的时间复杂度、空间复杂度均为O(1)
