L1, L2正则
正则的目的:规范模型参数,降低模型复杂度,减少过拟合
\[||w||_1 = \sum_1^N |w_i|
\]
\[||w||_2 = \sqrt {\sum_1^N |w_i|^2}
\]
拉格朗日对偶角度
模型经过训练后得到的W与b可能很小,也可能很大。
若W与b较大,在测试数据时,$ W*X $会放大输入中的误差与噪声。
因此,需要给W划定可行域范围,使其在训练时尽可能小。
-
\[min\ J(W,b,x) \\ s.t. ||w||_1 - C <= 0 \]
i.e., W 在高维空间中与原点的L1(曼哈顿)距离小于等于 C
2. $$ min\ J(W,b,x) \ s.t. ||w||_2 - C <= 0 $$
i.e., W 在高维空间中与原点的L2(欧几里得)距离小于等于 C
构造拉格朗日函数:
\[ \begin{aligned}
L(s,\lambda) &= J(s) + \lambda(||w||_1 - C) \\
&= J(w) + \lambda||w||_1 - \lambda C \\
\end{aligned}
\\
\\
\begin{aligned}
\hat{L}(s,\lambda) &= L(s,\lambda) + \lambda C\\
&= J(w) +\lambda||w||_1
\end{aligned}\]
其中,$ \hat{L}(s,\lambda)= J(w) +\lambda||w||_1$ 是常见的目标函数形式:$ min\ Obj=Cost+Regularization\ Term$
权重衰减角度
无正则项的情况下,权重更新:
\[w_{i+1} = w_i - \frac{\partial Obj}{\partial w_i} = w_i - \frac{\partial loss}{\partial w_i}
\]
有正则项(L2):
\[w_{i+1} = w_i - \alpha (\frac{\partial loss}{\partial w_i} + \lambda w_i) = w_i(1-\alpha \lambda)-\alpha \frac{\partial loss}{\partial w_i}
\]
其中,$ \alpha $ 为学习率
l1与l2的区别:
l1具有稀疏性。
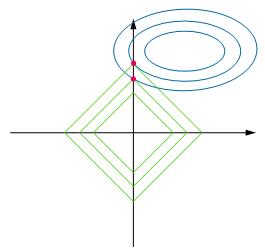
假设x,y轴代表两种特征,l1正则方法与loss的等高线更容易相切于y轴,在此情况下,x轴的值为0。等同于只有y轴特征起作用,x轴特征不起作用,实现特征间去耦合。

