【算法】网络流初步
参考资料
一、概念
网络流指的是在一个每条边都有容量的有向图中找到一种方案，使得源点到汇点的流量最大。
网络流问题常见的有三类，分别是最大流，费用流和最小割。
最大流顾名思义，表示的是在有向图中找到一种方案满足每条从源点到汇点的路径上的每条边的流量都不大于这条边的容量。比如下图：
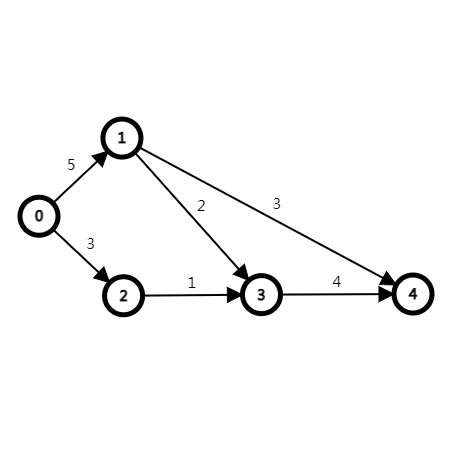
若源点是 \(0\)，汇点是 \(4\)，那么从源点到汇点能流过的最大流量便是 \(6\)。
费用流问题便是在一个不仅每条边有容量还有费用的有向图上，求出最大流的同时也求出最小花费。
最小割问题是在这张有向图上割掉任意条边，使得源点和汇点不相通，要求割掉的边数最小。实际上，最小割就等于最大流。
二、实现
首先介绍增广路的概念。增广路指的是一条从源点到汇点的路径，其中的每一条边的残量都为正数。而网络流算法的核心在于找增广路。但由于无法控制找到增广路的顺序，每次单纯找一条增广路的算法并不能适用于网络流问题。
我们依靠反悔贪心的思路，在原图内引入反向边。每次寻找增广路，同时将这条增广路上的每一条边的反边的容量都加上这条边的流量。之后如果选了一条路的反边，相当于没有选这条路，这样就达到了贪心的目的。
1. EK 算法
用 bfs 暴力寻找增广路，直到找不到为止，此时的答案就是这张图的最大流。时间复杂度为 \(O(nm^2)\)，其中 \(n\) 为点数，\(m\) 为边数。
当然，解决费用流问题时，bfs 也可以换成各种最短路径算法。下面给出的就是费用流代码。
bool spfa(){
for(int i=1;i<=n;i++){
dis[i]=(int)1e15;
vis[i]=false;
}
dis[s]=0;
queue<int>q;
q.push(s);
while(q.empty()==false){
int x=q.front();
q.pop();
vis[x]=false;
for(int i=head[x];i;i=edge[i].nex){
int v=edge[i].to,w=edge[i].w,va=edge[i].v;
if(w>0&&dis[v]>dis[x]+va){
dis[v]=dis[x]+va;
if(vis[v]==false){
vis[v]=true;
q.push(v);
}
}
}
}
if(dis[t]==(int)1e15) return false;
else return true;
}
int dfs(int x,int low){
vis[x]=true;
if(x==t){
ansi+=low;
return low;
}
int used=0;
for(int i=head[x];i;i=edge[i].nex){
int v=edge[i].to,w=edge[i].w,va=edge[i].v;
if(w>0&&(vis[v]==false||v==t)&&dis[v]==dis[x]+va){
int sum=dfs(v,min(low-used,edge[i].w));
if(sum==0) continue;
val+=va*sum;
edge[i].w-=sum;
edge[i^1].w+=sum;
used+=sum;
if(used==low) break;
}
}
return used;
}
void EK(){
while(spfa()){
vis[t]=true;
while(vis[t]==true){
memset(vis,0,sizeof(vis));
dfs(s,INT_MAX);
}
}
return;
}
2. Dinic 算法
Dinic 算法将有向图先用 bfs 跑出分层图，再在这个分层图上用 dfs 同时跑出多条增广路。时间复杂度为 \(O(n^2m)\)。
但事实上 Dinic 有一个常用的优化。我们发现在一次 dfs 中，它不得不遍历一篇当前点能到的所有边，即使这些边在前几次 dfs 中已经将流量跑满，没有再跑的可能了。所以我们引出当前弧优化，记录这一次跑满到了哪一条边，下一次直接从第一条没跑满的边开始遍历即可。
bool bfs(){
for(int i=1;i<=n;i++){
deep[i]=(int)1e9;
cur[i]=head[i];
vis[i]=q[i]=0;
}
tai=deep[s]=0;
q[++tai]=s;
while(tai!=0){
int x=q[tai--];
vis[x]=false;
for(int i=head[x];i;i=edge[i].nex){
int v=edge[i].to,w=edge[i].w;
if(deep[v]>deep[x]+1&&w>0){
deep[v]=deep[x]+1;
if(vis[v]==false){
q[++tai]=v;
vis[v]=true;
}
}
}
}
if(deep[t]==(int)1e9) return false;
return true;
}
int dfs(int x,int low){
if(x==t){
ansi+=low;
return low;
}
int used=0;
for(int i=cur[x];i;i=edge[i].nex){
cur[x]=i;
int v=edge[i].to,w=edge[i].w;
if(w>0&&deep[v]==deep[x]+1){
int sum=dfs(v,min(low-used,w));
if(sum==0) continue;
used+=sum;
edge[i].w-=sum;
edge[i^1].w+=sum;
if(used==low) break;
}
}
return used;
}
int dinic(){
while(bfs()==true){
dfs(s,(int)1e15);
}
return ansi;
}
三、应用
事实上，网络流问题的难点在于建模。而可以用网络流解决的问题一般而言数据范围都较小。对于建模，限制可以转化成网络流边上的容量。
网络流还可用于解决二分图最大匹配问题，我们将源点向左边的点都连一条容量为 \(1\) 的边，右边的点向汇点同样连一条容量为 \(1\) 的边，这样保证左右两边的点都只跑一次。
