【算法】拓扑排序
一、概念
拓扑排序是用于有向无环图的求顶点的一种排序序列的算法。这个序列有两种特点：
- 如果 A 能直接到 B，那么在这个序列中，A 在 B 前面。
- 每个节点都出现且只出现一次。
二、实现
对于特点二，只需要保证将所有节点只遍历一遍即可。
对于特点一，它等效于有依赖序列。
我们只需要找到没有路径指向它的节点 x，将它放进序列的首位。如果在这个序列中 y 还在 x 的前面，那么一定存在一条路径从 y 指向 x（根据特点一）。那么节点 x 就不是没有路径指向的节点了。
如下图，它的一种拓扑序列是 1 2 3。如果要选节点 2，那么由于 1 能直接到 2，所以在序列中 1 要在 2 前面。
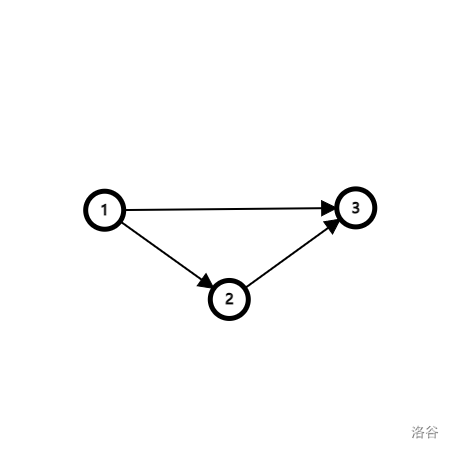
选了节点 1 后，它对节点 2 与 3 的限制也就解除了。由于节点 3 依赖于节点 2，节点 2的依赖节点 1 已经选了，所以下一步就是选节点 2。
时间复杂度：\(O(n+m)\)（\(n\) 是节点数，\(m\) 是总边数）
三、代码
const int N=1e4+5;//数据范围
int n,m;//节点数，边数
int head[N],tot;//链式前向星
int in[N];//入度，即有多少条路径连到节点 x
int topu[N],cnt;//记录拓扑序
void tsort(){
queue<int>q;
for(int x=1;x<=n;x++)
for(int i=head[x];i;i=edge[i].nex)
in[edge[i].to]++;//处理入度，一种比较好的处理方式是在建边的同时更新入度
for(int i=1;i<=n;i++)
if(in[i]==0)//找到没有依赖的点
q.push(i);
while(q.empty()==false){
int x=q.front();
topu[++cnt]=x;
q.pop();
for(int i=head[x];i;i=edge[i].nex){//由于这个点已经选了，那么后面点对它的依赖也就没有了
int v=edge[i].to;
in[v]--;
if(in[v]==0) q.push(v);
}
}
for(int i=1;i<=cnt;i++) cout<<topu[i]<<" ";
}
四、应用
感觉应用是最重要的（）
1. 判环/求环
拓扑排序适用于有向无环图，最后所有点的入度一定都是 0。
如果有环，那么最后会有点入度不为 0。反过来也成立。
如图，我们找不到一个入度为 0 的点，所以循环会直接跳出。而复杂的图只要包含环（也就是下面这种基本类型），就一定到最后找不到一个入度为 0 的点。
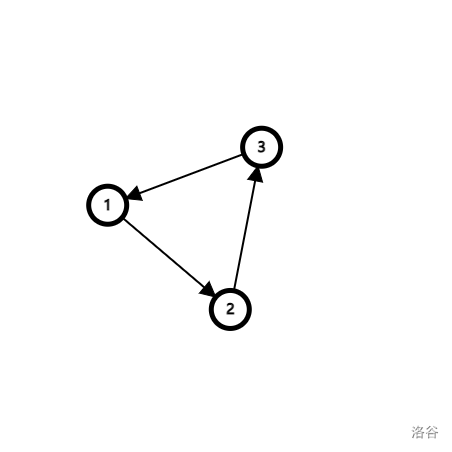
至于求最大/小环只需要拓扑排序后循环每一个环即可。
2. 依赖问题
比方说做 A 事情需要先做 B 事，那么可以建出一条从 B 到 A 的有向边，最后跑拓扑排序即可。
3. 求最长/短路
先将所有点按照拓扑序来排序，这样可以保证 dp 转移的正确性，也就是指向 \(x\) 的点要先更新。设点集 \(V_i\) 表示所有指向 \(i\) 的点，\(dp_{[i]}\) 表示到点 \(i\) 的最长路径，\(dis[j][i]\) 表示从 \(j\) 到 \(i\) 的边权。则 \(dp_{[i]}=\max\limits_{j\in V_i}(dp[j]+dis[j][i])\)。
最短路同理，只需要将 \(\max\) 换成 \(\min\) 即可。
例题部分咕了~
