【算法】Tarjan
参考资料:
图论相关概念 - OI WIKI | 强连通分量 - OI WIKI
一、概念
• 子图:
对一张图 \(G=(V,E)\),若存在另一张图 \(H=(V',E')\) 满足 \(V'\subseteq V\) 且 \(E'\subseteq E\),则称 \(H\) 是 \(G\) 的 子图 (subgraph),记作 \(H \subseteq G\)。——OI WIKI
通俗点说就是如果你能在图 G 中找到一部分和 H 一样,那么 H 就是 G 的子图。
或者这样理解,图 H 里面的所有边都能在 G 里面找到,那么就是子图了。
• 连通和可达
现在有两个点 x 和 y,如果在图 G 里能找到一条从 x 走到 y 的路径,那么就称之为 x 可达 y。如果图 G 是无向图的话,还可以说 x 与 y 连通。
现有三个定义:
-
如果无向图 G 里面任意两点都互相连通,那么图 G 就是连通图。
-
如果有向图 G 里面任意两点都互相可达,那么图 G 就是强连通的。
-
如果有向图 G 里面的有向边全部都为无向边后,任意两点都互相连通,那么图 G 就是弱连通的。
• (强/弱)连通分量
这是上一条的补充,也是这讲里面几乎是最重要的一个概念。
如果在无向图 G 中可以找到一个最大的连通子图 H,那么 H 就是 G 的连通分量
类似的,我们可以将连通分量的定义推广到强连通分量和弱连通分量上
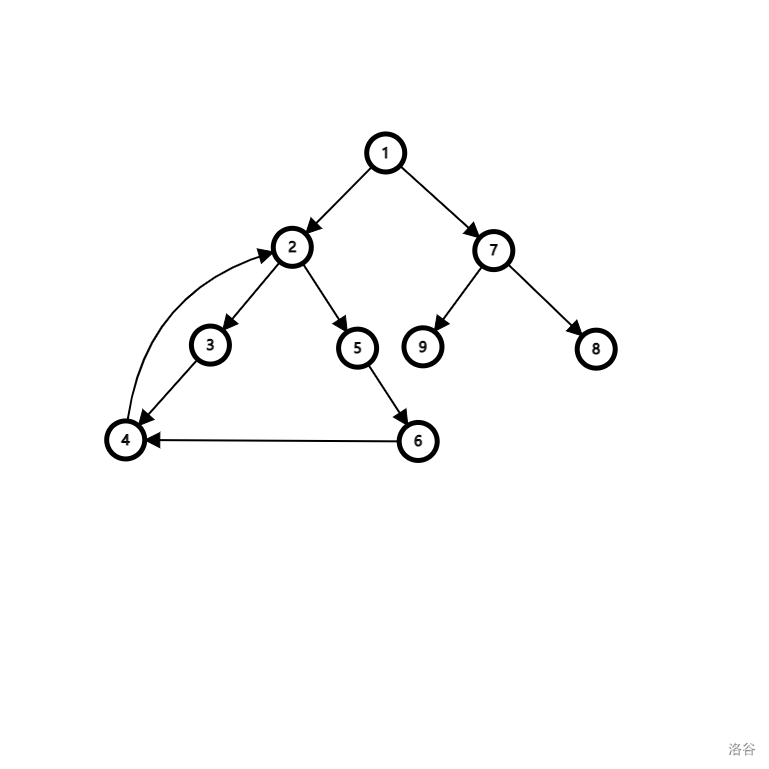
\(\tiny\text{图 1-1}\)
如上图 G,节点 2 3 4 构成的图不是 G 的强连通分量(不是最大的),但是节点 2 3 4 5 6 构成的图是 G 的强连通分量。当然点 1,7,8,9都分别是一个强连通分量
更通俗一点的,强连通分量可以理解为在有向图中找一个最大的环。
• Tarjan
Tarjan是一种快速求出有向图里面强联通分量的算法。
现在,我们将有向有环图抽象成 DFS 树,那么除了树边还会有其它边,比如下图:
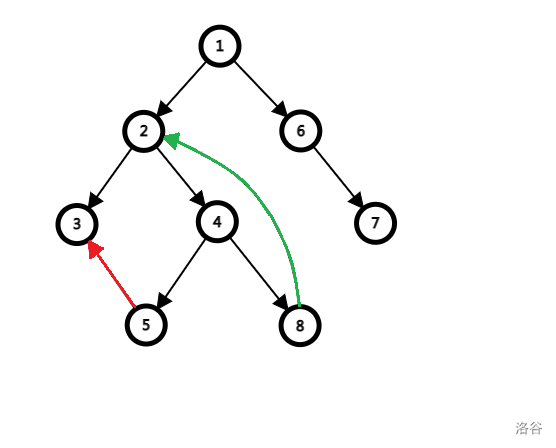
\(\tiny\text{图 1-2}\)
其中黑边为树边,红边和绿边为非树边。
特别的,我们规定红边为横插边,也就是非树边的两端没有父子关系;绿边为返祖边,也就是非树边的两端有父子关系。
但是,非树边的两端是节点 8 和节点 7 是不可能的,如果这样的话,当访问到节点 8 时为继续搜索节点 7 ,与现在这颗 DFS 树不符。
不难发现,绿边可以构成一个环,而红边不行。
而 Tarjan 算法一般用于缩点,也就是将一个强连通分量看做一个点,对结果并不影响。
二、实现
依旧要运用上面的 DFS 搜索树来实现 Tarjan
于是我们有了以下变量:
dfn[i] 表示 i 的 dfs 序
dn 表示 dfs 序数
当然还有链式前项星的那些变量。
判断两个点 u,v 强连通的条件:\(u\) 可达 \(v\),且 \(v\) 可达 \(u\)。
虽然听起来像废话,但我们可以从这个条件入手思考 Tarjan。
既然 \(u\) 要可达 \(v\) 的话,我们就直接遍历 \(u\) 所有可达的节点。
—— 于是
• 第一步:遍历 u
void tarjan(int x){
dfn[x]=++dn;//更新 dfn 数组
for(int i=head[x];i;i=edge[i].nex){
int nex=edge[i].to;
if(dfn[nex]==0){//如果之前没有被访问到
tarjan(nex);//访问
}
}
//当然这里会有一个判断 u 是否可构成强连通分量的语句,但现在不急
}
然后考虑什么时候 \(v\) 可达 \(u\)。
不难发现,当 \(v\) 有一条指向 \(u\) 或者 \(u\) 的祖先的时候,\(v\) 一定可达 \(u\)。
并且,一个节点只能在一个强连通分量里面,不妨用反证法证明一下,如果一个节点同时在两个强连通分量里面,那么这两个互相强连通的分量合在一起也是强连通的,并且比之前的分量大,与之前假设的不相符。
Q:怎么判断 \(u\) 节点是该强联通分量最先访问的节点呢?
再开一个数组存贮 \(low_{[u]}\) 表示 \(u\) 节点及 \(u\) 的子节点中的 \(dfn\) 最小值。
这样当 \(low_{[u]}=dfn_{[u]}\) 时就表示点 \(u\) 是最先访问的节点了。
——所以
-
第二步:更新 \(low\) 数组
void tarjan(int x){
low[x]=dfn[x]=++dn;//目前dfs序的最小值就是x的dfs序
stk[++top]=x;//入栈
inst[x]=true;
for(int i=head[x];i;i=edge[i].nex){
int nex=edge[i].to;
if(dfn[nex]==0){//如果子节点还没被访问过/还没入过栈
tarjan(nex);//先将它的子节点遍历,更新nex的low值
low[x]=min(low[x],low[nex]);//nex可能会连到x的祖先,所以进行更新的是low值
}
else if(inst[nex]==true){//之前就访问过了,说明它的dfs序比x要小
low[x]=min(low[x],dfn[nex]);//所以进行更新的是dfn值
}
/*
if(inst[nex]==false){
那么nex一定不属于u的强联通分量,直接continue
}
*/
}
}
Q:怎么确保 \(v\) 贡献给 \(u\) 的节点一定可以和 \(u\) 构成强连通分量呢?
考虑维护一个栈,记录 \(u\) 之后可以和它构成强连通分量的点。也就是说,每当遍历到一个点时,先判断一下它有没有已经属于一个强连通分量了,如果已经属于,那么就直接弹出栈。
由于不属于 \(u\) 强联通分量的点都已经被弹出栈了,所以当前在 \(u\) 之后入栈的元素都一定属于它的强联通分量。
——最后一步!
-
第三步:弹栈
inline void tarjan(int x){
/*前两步代码
low[x]=dfn[x]=++dn;
stk[++top]=x;
inst[x]=true;
for(int i=head[x];i;i=edge[i].nex){
int nex=edge[i].to;
if(dfn[nex]==0){
tarjan(nex);
low[x]=min(low[x],low[nex]);
}
else if(inst[nex]==true){
low[x]=min(low[x],dfn[nex]);
}
}
*/
if(dfn[x]==low[x]){//是当前强联通分量中最先访问的节点
cn++;//染色操作
while(stk[top]!=x){//在其后的都要弹出
int now=stk[top--];
inst[now]=false;
col[now]=cn;
}
int now=stk[top--];//自己也要弹出
inst[now]=false;
col[now]=cn;
}
}
三、时间复杂度
\(O(n)\),结束。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号