【做题笔记】初赛大全
CSP-S 2021
-
选择题
- 在 Linux 系统终端中,用于列出当前目录下所含的文件和子目录的命令为( )。
A. ls B. cd C. cp D. all
【知识点】操作系统基本概念及操作
ls:全称 list files,显示指定工作目录下之内容(列出目前工作目录所含之文件及子目录)。
cd:全称 change directory,切换当前目录。
cp:全称 copy file,复制文件或目录。
all:只可作为命令的参数
答案:A
- 二进制数 00101010 和 00010110 的和为( )。
A. 00111100 B. 01000000 C. 00111100 D. 01000010
【知识点】数的进制
竖式相加,满二进一即可。
答案:B
- 在程序运行过程中,如果递归调用的层数过多,可能会由于( )引发错误。
A. 系统分配的栈空间溢出
B. 系统分配的队列空间溢出
C. 系统分配的链表空间溢出
D. 系统分配的堆空间溢出
【知识点】递归函数
差不多是常识题,递归一个函数,相当于将其放进一个栈中。它的子问题解决了相当于栈顶元素被取出。
答案:A
- 以下排序方法中,( )是不稳定的。
A. 插入排序 B. 冒泡排序 C. 堆排序 D. 归并排序
【知识点】排序的基本概念
背诵题,稍微总结一下:快排、堆排、选择、希尔都不稳定,其余的排序都是稳定的。
答案:C
- 以比较为基本运算,对于 2n 个数,同时找到最大值和最小值,最坏情况下需要的最小的比较次数为( )。
A. 4n−2 B. 3n+1 C. 3n−2 D. 2n+1
【知识点】模拟法
可以先观察一下题目:\(2n\) 是一个很有趣的条件,于是我们不妨从这里入手。
将序列平均分为两个小序列,每次取出两个序列中相同位置的数进行比较,其中更小的数再与之前的最小值比较一次,更大的数与之前最大值比较一次,这样第一个位置上的只比较了一次,剩下所有位置上的数都比较了三次。也就是 \(1+3\times(n-1)=3n-2\)。
答案:C
- 现有一个地址区间为 0 到 10 的哈希表,对于出现冲突情况,会往后找第一个空的地址存储(到 10 冲突了就从 0 开始往后),现在要依次存储 (0,1,2,3,4,5,6,7) ,哈希函数为 \(h(x)=x^2\bmod11\) 。请问 7 存储在哈希表哪个地址中( )。
A. 5 B. 6 C. 7 D. 8
【知识点】哈希
按题意模拟即可,最后模拟出来的应该是:
| 位置 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 数字 | 0 | 1 | 5 | 2 | 4 | 6 | 7 | 3 |
答案:C
- G 是一个非连通简单无向图(没有自环和重边),共有 36 条边,则该图至少有( )个点。
A. 8
B. 9
C. 10
D. 11
【知识点】简单图
定理:若一个无向图有 \(n\) 个点,则它最多有 \(\dfrac{n(n-1)}{2}\) 条边(也就是当它是连通图的时候),随便手造几组例子就可以证明。
但是这道题说的是非连通,于是拿出一个点来孤立,最后得到 \(\dfrac{(n-1)(n-2)}{2}\) ,列个方程就行。
答案:C
8.令根结点的高度为 1,则一棵含有 2021 个结点的二叉树的高度至少为( )。
A. 10
B. 11
C. 12
D. 2021
【知识点】树——二叉树
定理:若根节点高度为 0,则高度为 \(k\) 的一棵树最多有 \(2^{k+1}-1\) 个节点。
由于这道题根节点高度为 1,那么列出不等式 \(2^k-1\ge2021\)即可。
答案:B
- 前序遍历和中序遍历相同的二叉树为且仅为( )。
A. 只有 1 个点的二叉树
B. 根结点没有左子树的二叉树
C. 非叶子结点只有左子树的二叉树
D. 非叶子结点只有右子树的二叉树
【知识点】树——树的遍历
知道前序遍历和中序遍历的定义就可以。
答案:D
10 .定义一种字符串操作为交换相邻两个字符。将 DACFEB变为 ABCDEF 最少需要( )次上述操作。
A. 7 B. 8 C. 9 D. 6
【知识点】模拟法、排序
用冒泡排序瞎模拟就行。
答案:A
- 有如下递归代码,则 \(solve(23,23)\) 的结果是( )。
A. 1
B. 7
C. 12
D. 22
solve(t, n):
if t=1 return 1
else return 5 * solve(t-1,n) mod n
【知识点】初等数论
当然直接模拟应该也可以求出答案,但容易挂。
不考虑每一次递归里的取模运算,只在最后一步取模,即求 \(5^{t-1}\bmod n\)。
用费马小定理 \(a^{p-1}\equiv1\pmod p\)可以求出 \(5^{22}\equiv1\pmod {23}\)。
答案:A
- 斐波那契数列的定义为: \(F_1=1,F_2=1,F_n=F_{n−1}+F_{n−2}(n\ge3)\) 。现在用如下程序来计算斐波那契数列的第 n 项,其时间复杂度为( )。
A. \(O(n)\)
B. \(O(n^2)\)
C. \(O(2^n)\)
D. \(O(n\log n)\)
F(n):
if n<=2 return 1
else return F(n-1) + F(n-2)
【知识点】复杂度
感觉正常时间复杂度稍微有点麻烦,不妨用一种抽象的方式来思考。
画出一颗递归二叉树,每递归一次,总操作数就要乘以 \(2\),最后一共大约有 \(2n\) 次(?),故总的时间复杂度去掉常数后就是 \(O(2^n)\)。
答案:C
- 有 8 个苹果从左到右排成一排,你要从中挑选至少一个苹果,并且不能同时挑选相邻的两个苹果,一共有( )种方案。
A. 36 B. 48 C. 54 D. 64
【知识点】组合数学,枚举
可以将暴力枚举优化一下,只分别枚举选 1,2,3,4 个的情况,其中有些情况内的方案数可以用基础的加法原理求出来。
考虑用动态规划的思想,设 \(f_i\) 表示包括不取在内的有 \(i\) 个苹果的总方案数。
稍微枚举一下或者稍微推一下得出状态转移方程:\(f_i=f_{i-1}+f_{i-2}\),于是就可以很容易地得出 \(f_8=55\),最后再减去不选的方案即是答案。
答案:C
- 设一个三位数 \(n=\overline {abc}\) ,其中 a,b,c 均为 1 到 9 之间的整数,若以 a,b,c 作为三角形的三条边可以构成等腰三角形(包括等边),则这样的 n 有( )个。
A. 81 B. 120 C. 165 D. 216
【知识点】枚举法
枚举等腰三角形的腰,求出每种情况即可。
答案:C
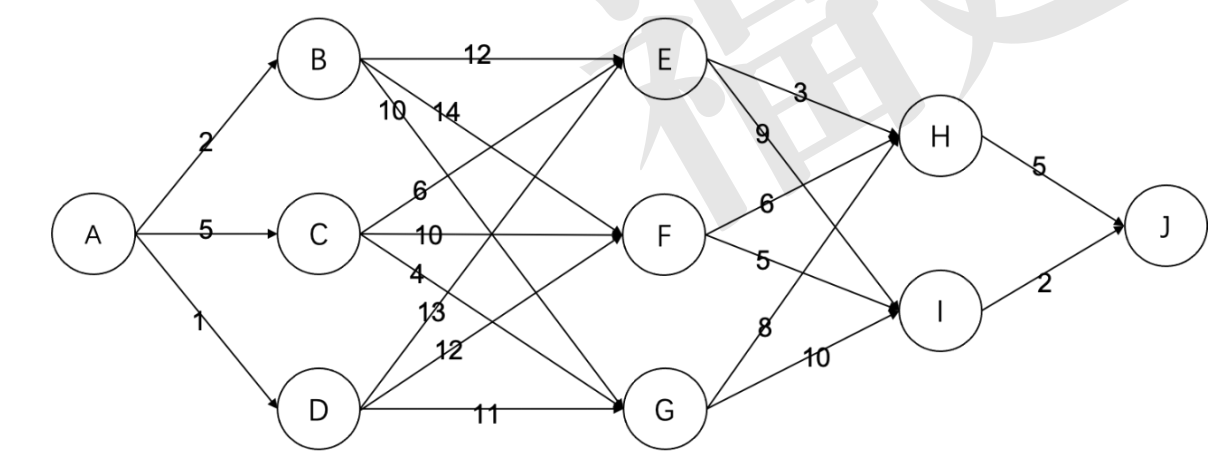
- 有如下的有向图,节点为 A, B, … , J, 其中每条边的长度都标在图中。则节点 A 到节点 J 的最短路径长度为( )
A. 16 B. 19 C. 20 D. 22
【知识点】模拟法
模拟最短路径算法即可。
答案:B
-
程序阅读

完全看不懂
大概的意思是给出两个以 \(a,b,c\) 为球心,\(d\) 为半径的球,求它们相交的体积。
- 将第 21 行中 t 的类型声明从 int 改为 double ,不会影响程序运行的结果。( )
看到 \(a1,a2,b1,b2,c1,c2,d1,d2\) 以及 \(sq\) 函数都是 \(int\) 类型的,\(t\) 也没有任何取整之类的操作,所以不会影响。
答案:正确
- 将第 26、27 行中的/ sqrt(t) / 2替换为/ 2 / sqrt(t),不会影响程序运行的结果。( )
很明显,\(sqrt\) 函数和除法运算都会向下取整,所以不能替换顺序。
答案:错误
- 将第 28 行中的x * x改成sq(x)、y * y改成sq(y) ,不会影响程序运行的结果。( )
注意 \(sq\) 函数的类型是 \(int\),而 \(x,y\) 类型的都是 \(double\),故这样操作会导致精度问题。
答案:错误
- 当输入为0 0 0 1 1 0 0 1时,输出为1.3090。( )
正常来说,只要你会三角函数,这道题可以模拟出来,差不多是 \(\dfrac{5\pi}{12}\)。
答案:正确
- 当输入为1 1 1 1 1 1 1 2时,输出为( )。
A. 3.1416 B. 6.2832 C. 4.7124 D. 4.1888
这时候两个球的位置相等,只有半径不等,此时它们的体积交就是较小的球的体积。将 \(r=1\) 代入 \(V=\frac{4}{3}\pi r^3\)求出答案。
答案:D
- 这段代码的含义为( )。
A. 求圆的面积并 B. 求球的体积并
C. 求球的体积交 D. 求椭球的体积并
A 选项一眼就可以排除,D 选项 根据蒙题大法 如果是的话,公式应该会更复杂,再根据代码中的 \(min\) 可得出是体积交。
答案:C


分析一下代码可得出这是在求最大字段和,在 \(solve2()\) 的返回中包含了这几种情况:
\(solve2(h,j)\):最大字段和都在左半段
\(solve2(j+1,m)\):最大字段和都在右半段
\(wh+wm\):最大字段和横跨了左半段和右半段
- 程序总是会正常执行并输出两行两个相等的数。( )
solve1 和 solve2 本质上是相同的。
答案:正确
- 第 28 行与第 38 行分别有可能执行两次及以上。( )
这两行代码被执行到的时候,当且仅当 \(n\le0\),并且也只会执行一次。
答案:错误
- 当输入为5 -10 11 -9 5 -7时,输出的第二行为“7”。( )
这里的最大字段和为 11。
答案:错误
- solve1(1, n) 的时间复杂度为( )。
A. \(O(\log n)\) B. \(O(n)\) C. \(O(n\log n)\) D. \(O(n!)\)
\(T(n)=1+2T(\dfrac{n}{2})=1+(2+4T(\dfrac{n}{4}))=...=O(n)\)
答案:B
- solve2(1, n) 的时间复杂度为( )。
A. \(O(\log n)\) B. \(O(n)\) C. \(O(n\log n)\) D. \(O(n!)\)
\(T(n)=n+2T(\dfrac{n}{2})=n+(n+4T(\dfrac{n}{4}))=...=O(n\log n)\)
答案:C
- 当输入为10 -3 2 10 0 -8 9 -4 -5 9 4时,输出的第一行为( )。
A. 13 B. 17 C. 24 D. 12
算最大字段和得出 \(2+10+0+(-8)+9+(-4)+(-5)+9+4=17\)
答案:B


大概就是 base64 加密和解密的过程,其中 0 是加密,1 是解密。
- 程序总是先输出一行一个整数,再输出一行一个字符串。( )
有可能解密出来的字符包含回车符“\n”,导致后面有多行(?)
答案:错误
- 对于任意不含空白字符的字符串 str1,先执行程序输入0 str1,得到输出的第二行记为 str2;再执行程序输入1 str2,输出的第二行必为 str1。( )
一个加密过去,另一个解密回来,答案一定相同。
答案:正确
- 当输入为1 SGVsbG93b3JsZA==时,输出的第二行为HelloWorld。( )
模拟后得出解密的字符串应为 Helloworld。(经典大小写出错)
答案:错误
- 设输入字符串长度为 n,encode 函数的时间复杂度为( )。
A. \(O(\sqrt{n})\) B. \(O(n)\) C. \(O(n\log n)\) D. \(O(n!)\)
这个算比较简单的时间复杂度分析了,只有一重循环。
答案:B
- 输出的第一行为( )。
A. 0xff B. 255 C. 0xFF D. -1
一开始初始化为 0xff,最后转成 int 类型的话便是 -1。
答案:D
- 当输入为0 CSP2021csp时,输出的第二行为( )。
A. Q1NQMjAyMWNzcAv= B. Q1NQMjAyMGNzcA==
C. Q1NQMjAyMGNzcAv= D. Q1NQMjAyMWNzcA==
可恶又要手推。
答案:D
-
程序填空


\(F_i\):可行的方案中 4 的个数
\(vis_i\):最优解是否确定
对于一个数,它可以通过三种情况转移过来,其中 4 的个数都是两个数中 4 的个数的和:
- 分解成两个数相加的形式
- 分解成两个数相减的形式
- 分解成两个数相除的形式
- ①处应填( )
A. F[4] = 0 B. F[1] = 4 C. F[1] = 2 D. F[4] = 1
状态的转移一定是从最小值转移过来的。
答案:D
- ②处应填( )
A. !Vis[n] B. r < n C. F[M] == INT_MAX D.F[n] == INT_MAX
结束条件的判断,程序结束当且仅当最优解已经确定。
答案:A
- ③处应填( )
A. F[i] == r B. !Vis[i] && F[i] == r
C. F[i] < F[x] D. !Vis[i] && F[i] < F[x]
选择现在应该转移什么数。首先这个数的最优解还未确定,其次它应该是所有数里面 \(F\) 值最小的,这样可以保证它无法再被更新,当前值即是最优解。
答案:D
- ④处应填( )
A. F[i] < F[x] B. F[i] <= r C. Vis[i] D. i <= x
更新的两个值的确定。如果要保证此次更新是有效的,那么两个转移的值都需要是最优解。
答案:C
后面的题就直接看参考资料里的博客吧!


 浙公网安备 33010602011771号
浙公网安备 33010602011771号