个人项目——北京地铁最短路径规划
北京地铁出行线路规划项目
github地址：github
项目概要
以下是北京地铁线路总图，本项目的受众可以通过本软件，获得北京市地铁出行最便捷，最快速的线路推荐。
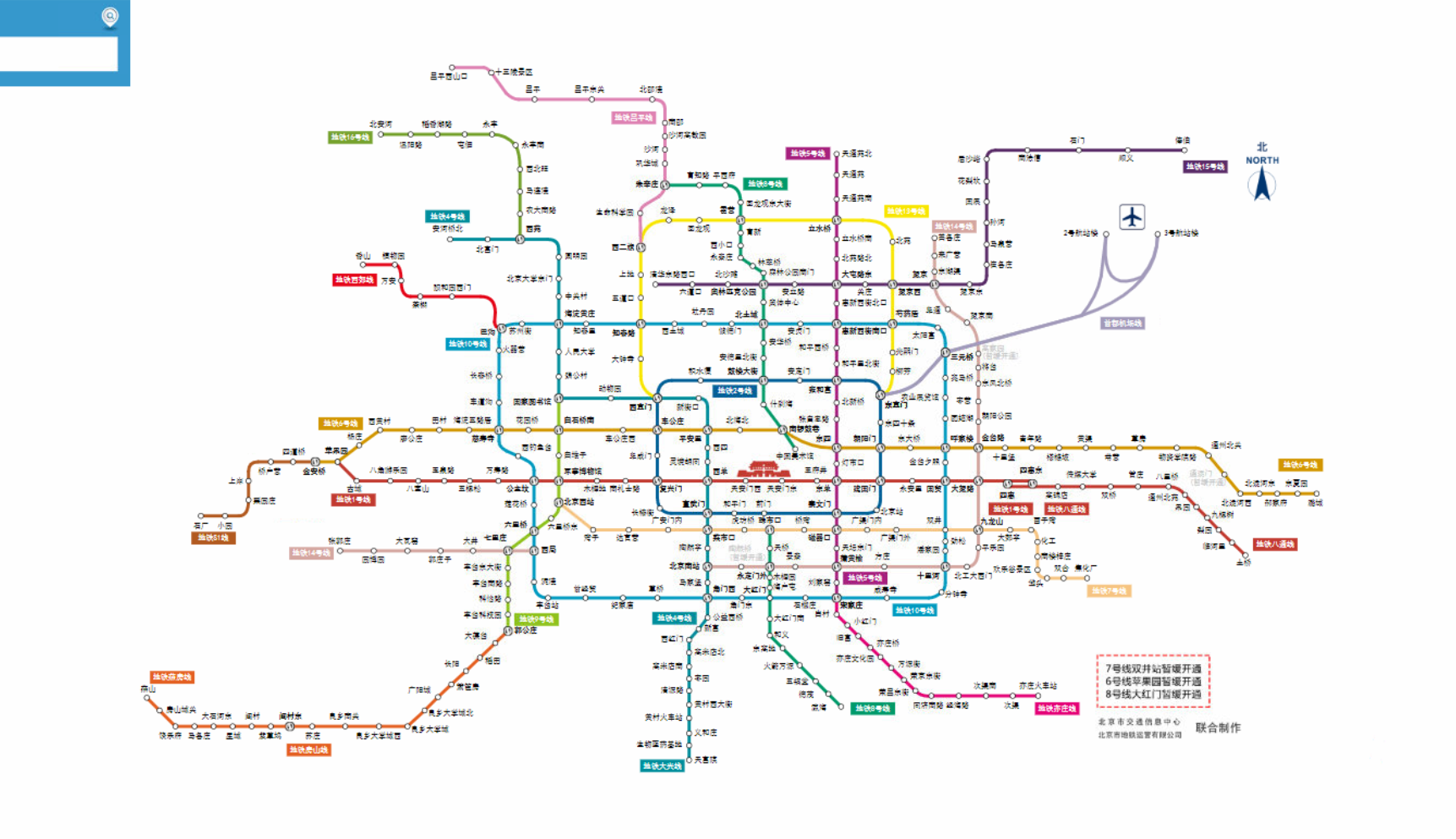
需求分析
- 实现一个帮助进行地铁出行路线规划的命令行程序。
- 支持查询线路的所有站点。
- 支持查询到某终止站点的途径最少站点的路线。
- 能正确处理输入的参数，且具备一定健壮性
项目psp计划
| PSP | Personal Software Process Stages | Time |
|---|---|---|
| Planning | 计划 | |
| · Estimate | · 估计这个任务需要多少时间 | 1h |
| Development | 开发 | |
| · Analysis | · 需求分析(包括学习新技术) | 1h |
| · Design Spec | · 生成设计文档 | 2h |
| · Design Review | · 设计复审(和同事审核设计文档) | 1h |
| · Coding Standard | · 代码规范(为目前的开发制定合适的规范) | 1h |
| · Design | · 具体设计 | 1h |
| · Coding | · 具体编码 | 2h |
| · Code Revieq | · 代码复审 | 1h |
| · Test | · 测试(自我测试，修改代码，提交修改) | 1h |
| Reporting | 报告 | |
| · Test Report | · 测试报告 | 1h |
| · Size Measurement | · 计算工作量 | 1h |
| · Postmortem & Process Improvement Plan | · 事后总结,并提出过程改进计划 | 1h |
| 合计 | 14h |
地铁文本储存方式
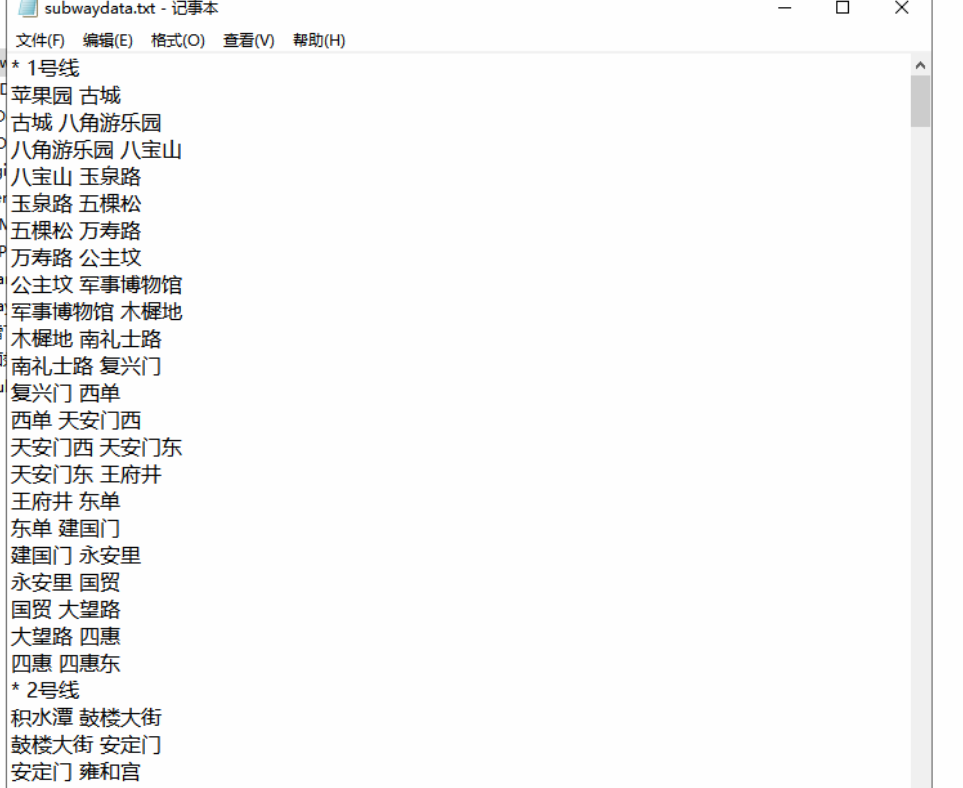
该文本以格式化的方法，输入每条线路的站点，以边的顺序依次输入，这符合一般人的考虑方式。每一行读入2个字符串A，B。当A读入是*时，表示B是线路，当A读入是文字时，表示A，B都是站点。
建图方式
在model包中包含6个类：
- Edge类存储2站之间的每一条边
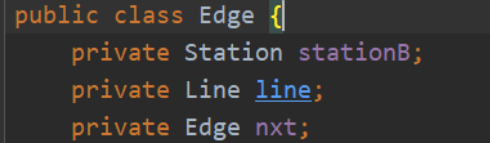，含有下一个站点的信息stationB，属于的地铁线路line，之后的下一条边nxt。 -
Line类存储每一条线路的信息
，线路的名字name，线路中包含的站点lin -
station类存储每一站的信息
，站点的名字name，该站点的第一条出边。 -
graph类存储每张图的信息
stationMap表示去重后的所有站点，lineList表示所有的线路。
主算法分析
Main类中包含5个方法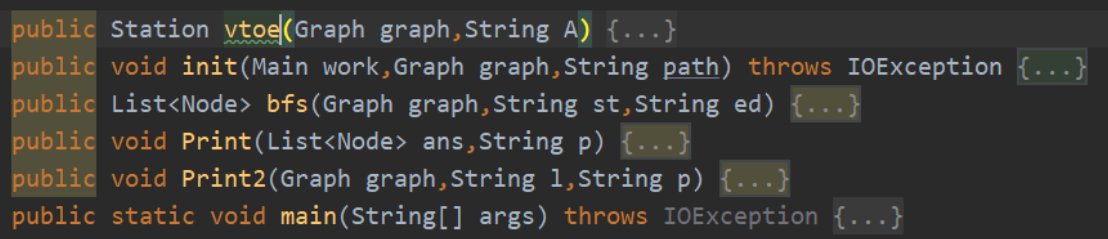
-
-
-
public void init(Main work,Graph graph,String path)方法，用来根据读入的站点txt文件初始化所有的站点，并建图（邻接表）。
public void init(Main work,Graph graph,String path) throws IOException { path="F:\\"+path; //预设在F盘 String filepath=path; FileReader fileReader=new FileReader(filepath); BufferedReader bufferedReader=new BufferedReader(fileReader); String line=bufferedReader.readLine(); //文件读入 while (line!=null) { String A,B; //将入读的一行字符串划分成有明确意义的A、B两个字符串。 A=""; B=""; int i=0; for (i=0;i<line.length();i++) { char k=line.charAt(i); if (k!=' ') { A=A+k; } else { break; } } i++; for (;i<line.length();i++) { char k=line.charAt(i); B=B+k; } if (A.equals("*")) { Line line1=new Line(); line1.setName(B); graph.lineList.add(line1); } else { Line line1=graph.lineList.get(graph.lineList.size()-1); Station Ast=work.vtoe(graph,A); //获取A站点判重后的唯一Station Station Bst=work.vtoe(graph,B); //获取B站点判重后的唯一Station if (line1.getLine().size()==0) { line1.getLine().add(Ast.getName()); line1.getLine().add(Bst.getName()); } else { line1.getLine().add(Bst.getName()); } Edge edge1=new Edge(); //使用邻接表建图，建成双向边。 edge1.setLine(line1); edge1.setStationB(Bst); edge1.setNxt(graph.stationMap.get(A).getFstedge()); graph.stationMap.get(A).setFstedge(edge1); Edge edge2=new Edge(); edge2.setLine(line1); edge2.setStationB(Ast); edge2.setNxt(graph.stationMap.get(B).getFstedge()); graph.stationMap.get(B).setFstedge(edge2); } line=bufferedReader.readLine(); } bufferedReader.close(); fileReader.close(); }
-
public Station vtoe(Graph graph,String A)用来判重所有的站点，使用map来hash处理。
public Station vtoe(Graph graph,String A) { if (!graph.stationMap.containsKey(A)) { Station newst=new Station(); newst.setName(A); graph.stationMap.put(A,newst); } return graph.stationMap.get(A); }
- public List<Node> bfs(Graph graph,String st,String ed)算法主体，采用BFS广度优先搜索。之所以采用这个算法，是因为如果将所有的边等价成1，那么所谓的一些求最短路的算法的效率都与bfs类似，况且bfs本就具备求扩展最短层数的性质（即本项目中的站数最少）
public List<Node> bfs(Graph graph,String st,String ed) { Station besta = graph.stationMap.get(st); Station edsta = graph.stationMap.get(ed); List<Node> ans = new ArrayList<Node>(); List<Node> allpathend = new ArrayList<Node>(); LinkedList<Node> que = new LinkedList<Node>(); LinkedList<Node> tmp = new LinkedList<Node>(); Set<String> inq = new HashSet<String>(); Node q = new Node(); q.setSt(besta); que.push(q); Edge edge = new Edge(); while (!que.isEmpty()) { int size = que.size(); int flag = 1; for (int i=0;i<size;i++) //一层一层直接扩展 { Node p = que.poll(); tmp.push(p); } for (int i = 0; i < size; i++) { Node p = tmp.poll(); inq.add(p.getSt().getName()); if (p.getSt().equals(edsta)) { flag = 0; //flag表示当前这一层已经能到终点，所以把flag=0使其不再扩展下一层。 allpathend.add(p); //allpathend用于判断在当前距离下，能走到终点的所有方法。用于判断站数最少的情况下，换乘最少。 continue; } Station pp = p.getSt(); edge = pp.getFstedge(); while (edge.getStationB() != null) { Station qq = edge.getStationB(); if (inq.contains(qq.getName())) { edge = edge.getNxt(); continue; } Node nxt = new Node(); nxt.setSt(edge.getStationB()); nxt.setLine(edge.getLine()); nxt.setPre(p); que.push(nxt); edge=edge.getNxt(); } } if (flag == 0) break; } int hc = 1000000; for (Node k : allpathend) { //距离相同的所有线路中找换乘最少的 List<Node> ppath = new ArrayList<Node>(); int phc = 0; String nxtline = k.getLine().getName(); ppath.add(k); while (k.getPre() != null) { k = k.getPre(); if(k.getPre()==null){ ppath.add(k); break; } if (!k.getLine().getName().equals(nxtline)) phc++; ppath.add(k); } if (phc < hc) { ans = ppath; hc=phc; } } return ans; }
-
public void Print(List<Node> ans,String p)用于输出两站之间的最短线路
public void Print(List<Node> ans,String p) { FileWriter fw = null; String path="F:\\"+p; try { File f=new File(path); fw = new FileWriter(f, false); } catch (IOException e) { e.printStackTrace(); } PrintWriter pw = new PrintWriter(fw); pw.println("一共经过"+ans.size()+"站路"); pw.println(ans.get(ans.size()-1).getSt().getName()); for (int i=ans.size()-2;i>=1;i--) { Node now=ans.get(i); Node nxt=ans.get(i-1); if (!now.getLine().getName().equals(nxt.getLine().getName())) { pw.print(now.getSt().getName()); pw.println("(换乘"+nxt.getLine().getName()+")"); } else { pw.println(now.getSt().getName()); } } pw.println(ans.get(0).getSt().getName()); pw.flush(); try { fw.flush(); pw.close(); fw.close(); } catch (IOException e) { e.printStackTrace(); } }
-
public void Print2(Graph graph,String l,String p)用于输出每条线路的站点。
public void Print2(Graph graph,String l,String p) { FileWriter fw = null; String path="F:\\"+p; try { File f=new File(path); fw = new FileWriter(f, false); } catch (IOException e) { e.printStackTrace(); } PrintWriter pw = new PrintWriter(fw); for (Line i:graph.lineList) { if (i.getName().equals(l)) { for (String j:i.getLine()) { pw.println(j); } break; } } pw.flush(); try { fw.flush(); pw.close(); fw.close(); } catch (IOException e) { e.printStackTrace(); } }
-
-
测试用例
编译所有的文件
测试方法一：
结果：
测试二：
结果：
输入错误情况：
