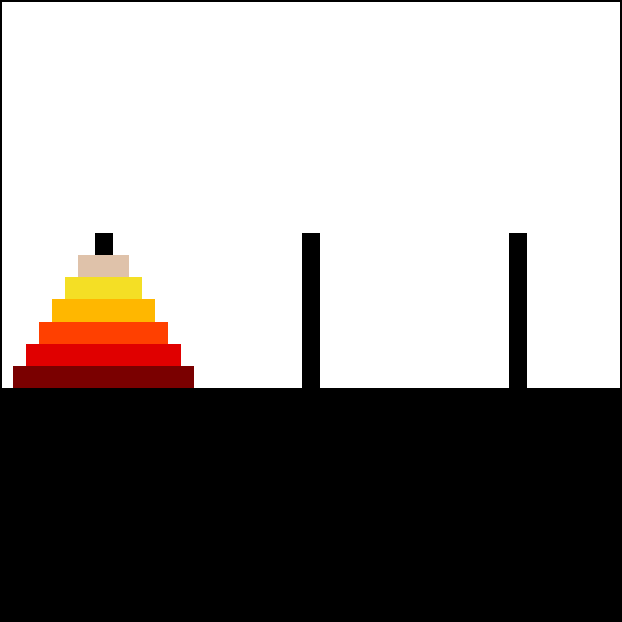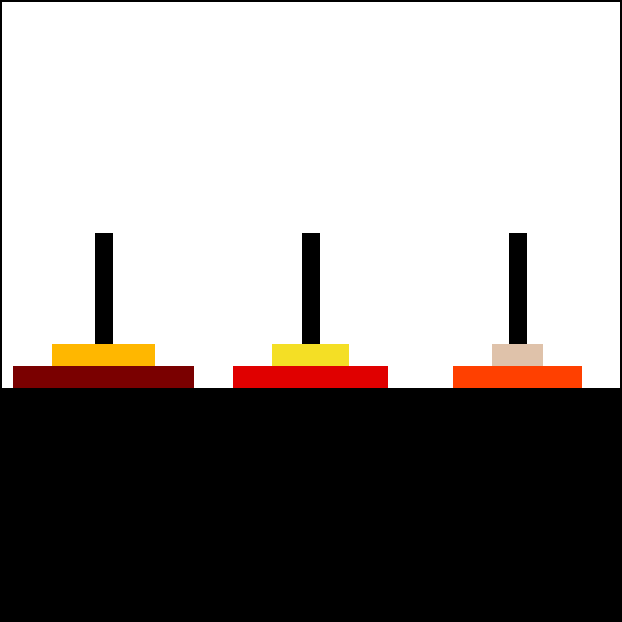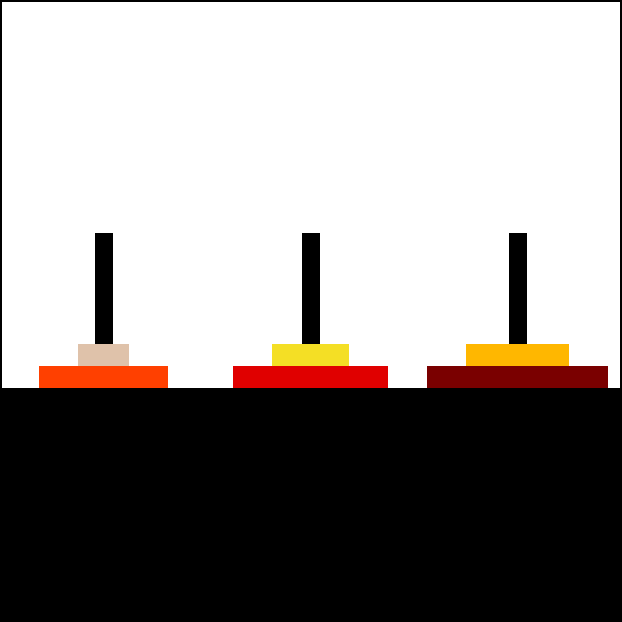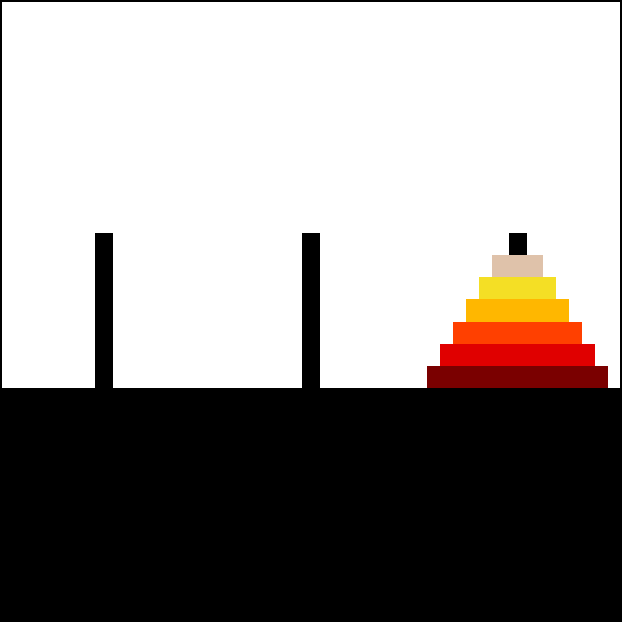汉诺塔问题

The Tower of Hanoi (also called the Tower of Brahma or Lucas' Tower and sometimes pluralized) is a mathematical game or puzzle. It consists of three rods and a number of disks of different sizes, which can slide onto any rod. The puzzle starts with the disks in a neat stack in ascending order of size on one rod, the smallest at the top, thus making a conical shape.

The objective of the puzzle is to move the entire stack to another rod, obeying the following simple rules:

• Only one disk can be moved at a time.
• Each move consists of taking the upper disk from one of the stacks and placing it on top of another stack or on an empty rod.
• No disk may be placed on top of a smaller disk.

Animation of an iterative algorithm solving 6-disk problem

With 3 disks, the puzzle can be solved in 7 moves. The minimal number of moves required to solve a Tower of Hanoi puzzle is 2^n − 1, where n is the number of disks.

思路：

1.只有一个盘子，则直接从第一个杆子移到第三个杆子上

2.超过一个盘子（设为N个）

　　（1）先把第一个杆子的N-1个，移到第二个杆子上

　　（2）再把第一个杆子最大的那个移到第三个杆子上去

　　（3）同理，对第二个杆子的N-1个盘子作为开始杆进行递归。

代码：

#include <iostream>
 
using namespace std;
 
void hanoi(int N,int start,int helper,int destination){
    if(N==1)
        cout<<"Move "<<start<<" to "<<destination<<endl;
    else{
        hanoi(N-1,start,destination,helper);
        hanoi(1,start,helper,destination);
        hanoi(N-1,helper,start,destination);
    }
}
 
int main()
{
    int N=10;
    hanoi(10,1,2,3);
    return 0;
}