[转] 图解attention实现细节

小图画的明儿白儿的

from:https://zhuanlan.zhihu.com/p/44731789

 

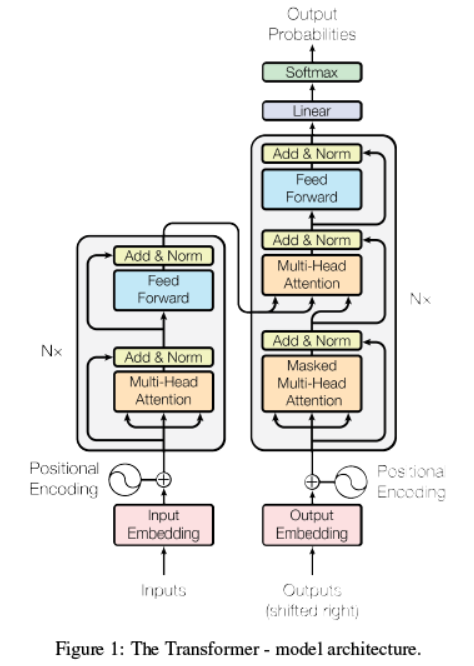
上图是attention模型的总体结构，包含了模型所有节点及流程（因为有循环结构，流程不是特别清楚，下文会详细解释）；模型总体分为两个部分：编码部分和解码部分，分别是上图的左边和右边图示；以下选取翻译情景，以模型训练为例解释整个过程；

训练样本：原文译文(一一对应)

 

编码部分（inputs）：

1. Input embedding:

1.1 将原文的所有单词汇总统计频率，删除低频词汇（比如出现次数小于20次的统一

定义为’<UNK>’）；此时总共选出了假设10000个单词，则用数字编号为0~9999，一一对应，定义该对应表为word2num；然后用xaviers方法生成随机矩阵Matrix ：10000行N列（10000行是确定的，对应10000个单词，N列自定义）；这样就可以将10000个不同的单词通过word2num映射成10000个不同的数字（int），然后将10000个不同的数字通过Matrix映射成10000个不同的N维向量（如何映射？比如数字0，3，经过 Matrix映射分别变为向量Matrix[0],Matrix[3]，维度为N维）；这样，任何一个单词，都可以被映射成为唯一的一个N维向量；

 

 

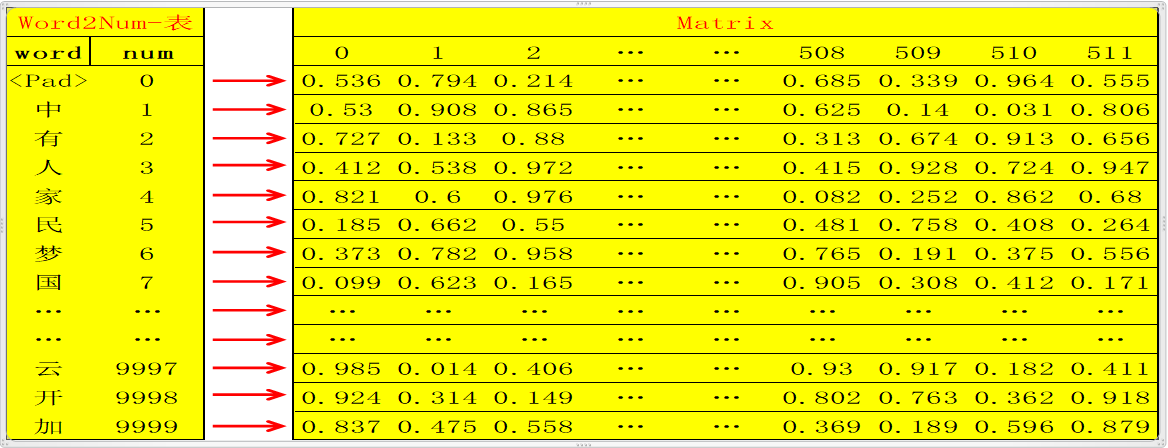
Note：此处N自定义为512

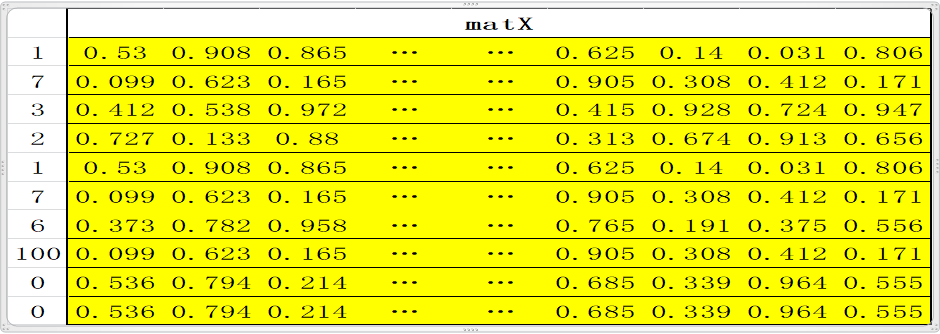
1.2 翻译的时候是一个句子一个句子的翻译，所以需要定义一个句子的标准长度，比如10个单词；如果一句话不足10个单词则用0填充（对应的word即word2num表中的<Pad>），如果多了，删掉；这样一句话就是标准的10个单词；比如句子 “中国人有中国梦。”，这句话共有八个字（最后一个是结束符），经过word2num变为一列X：[1,7,3,2,1,7,6,100,0,0](注：100代表的word是结束符),X经过Matrix映射为10行N列的矩阵matX= [Matrix[1], Matrix[7], Matrix[3], Matrix[2] , Matrix[1] , Matrix[7] , Matrix[6], Matrix[100] , Matrix[0] , Matrix[0]]; embedding 到此基本结束，即完成了将一句话变为 一个矩阵，矩阵的每一行代表一个特定的单词；此处还可以scale一下，即matX*N**(1/2);

 

 

2. Positional encoding:

2.1 单词在句子中的不同位置体现了不同信息，所以需要对位置进行编码，体现不同的信息情况，此处是对绝对位置进行编码，即位置数字0，1，2，3，…N等，进行运 算编码，具体编码如下：

2.1.1 对于句子中的每一个字，其位置pos∈[0,1,2,…,9](每句话10个字),每个字是N（512）维向量，维度 i （i∈[ 0,1,2,3,4,..N]）带入函数

 

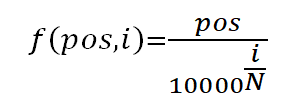
2.1.2 经过如上函数运行一次后，获得了一个10行N列的矩阵matP；每一行代表一个绝对位置信息，此时matP的shape和matX的shape相同；

 

 

2.1.3 对于矩阵matP的每一行，第0，2，4，6,...等偶数列上的值用sin()函数激 活，第1，3，5，。。。等奇数列的值用cos()函数激活，以此更新matP；即 matP[:,0::2]=sin(matP[:,0::2]), matP[:,1::2]=cos(matP[:,1::2])；

 

 

2.2 至此positional encoding结束，最后通常也会scale一次，即对更新后的matP进行matP*N**(1/2)运算，得到再次更新的matP，此时的matP的shape还是和matX相 同；然后将matP和matX相加即matEnc=matP+matX，矩阵matEnc其shape=[10，512]；

3. Multi-head attention---add&Norm---Feed Forward---add&norm 循环单元

3.1 然后matEnc进入模型编码部分的循环，即Figure1中左边红色框内部分，每个循环 单元又分为4个小部分：multi-head attention, add&norm, feedForward, add&norm；

3.2 Multi-head attention

 

 

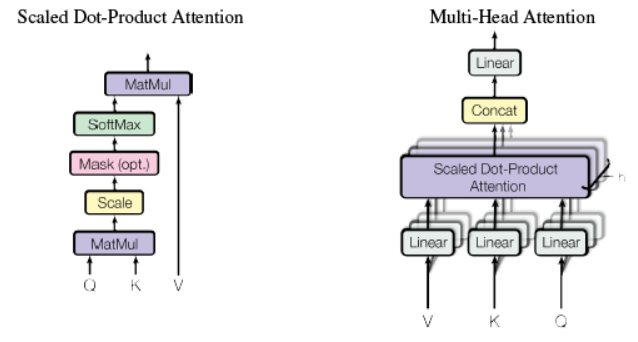
3.2.1 Multi-head attention 由三个输入，分别为V，K，Q，此处V=K=Q=matEnc（在解码部分multi-head attention中的VKQ三者不是这种关系）;

3.2.2 首先分别对V，K，Q三者分别进行线性变换，即将三者分别输入到三个单层神经网络层，激活函数选择relu，输出新的V，K，Q（三者shape都和原来shape相同，即经过线性变换时输出维度和输入维度相同）；

3.2.3 然后将Q在最后一维上进行切分为num_heads(假设为8)段，然后对切分完的矩阵在axis=0维上进行concat链接起来；对V和K都进行和Q一样的操作；操作后的矩阵记为Q_,K_,V_；

 

 

 

 

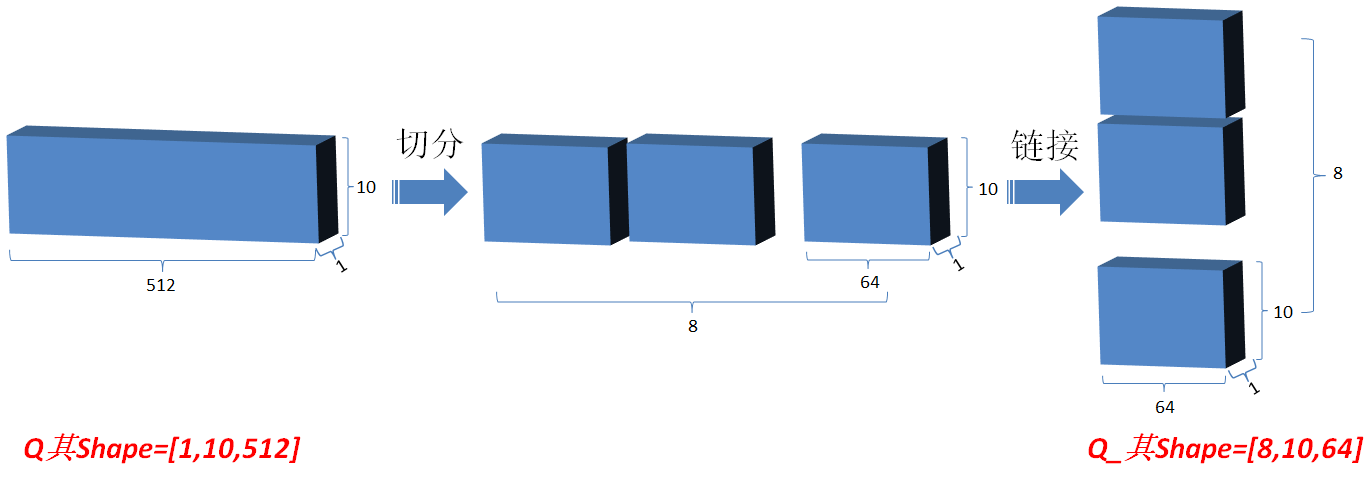
3.2.4 Q_矩阵相乘 K_的转置（对最后2维），生成结果记为outputs，然后对outputs 进行scale一次更新为outputs；此次矩阵相乘是计算词与词的相关性，切成多个num_heads进行计算是为了实现对词与词之间深层次相关性进行计算；

 

 

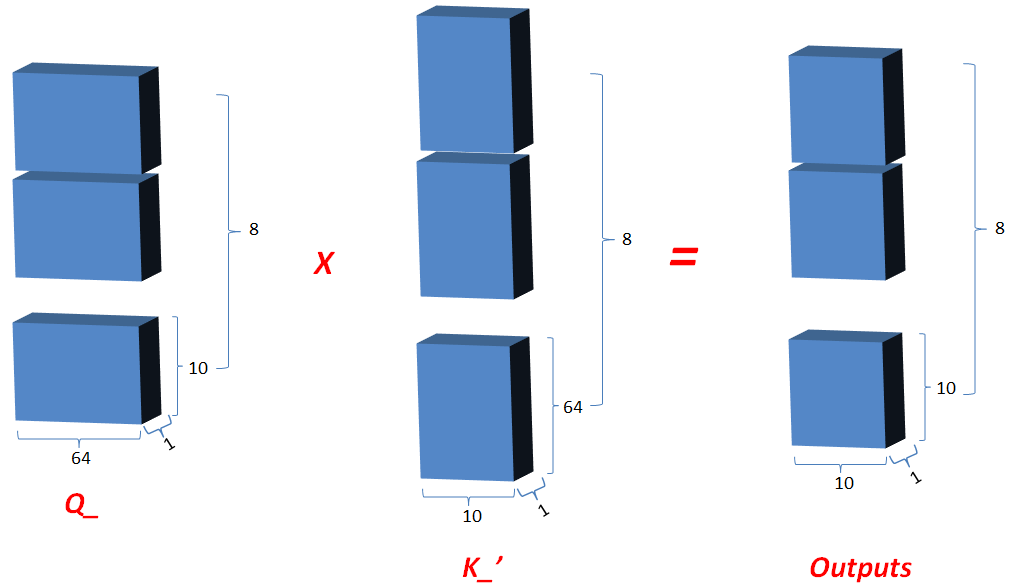
3.2.5 对outputs进行softmax运算，更新outputs，即outputs=softmax(outputs);

3.2.6 最新的outputs（即K和Q的相关性） 矩阵相乘 V_， 其值更新为outputs；

 

 

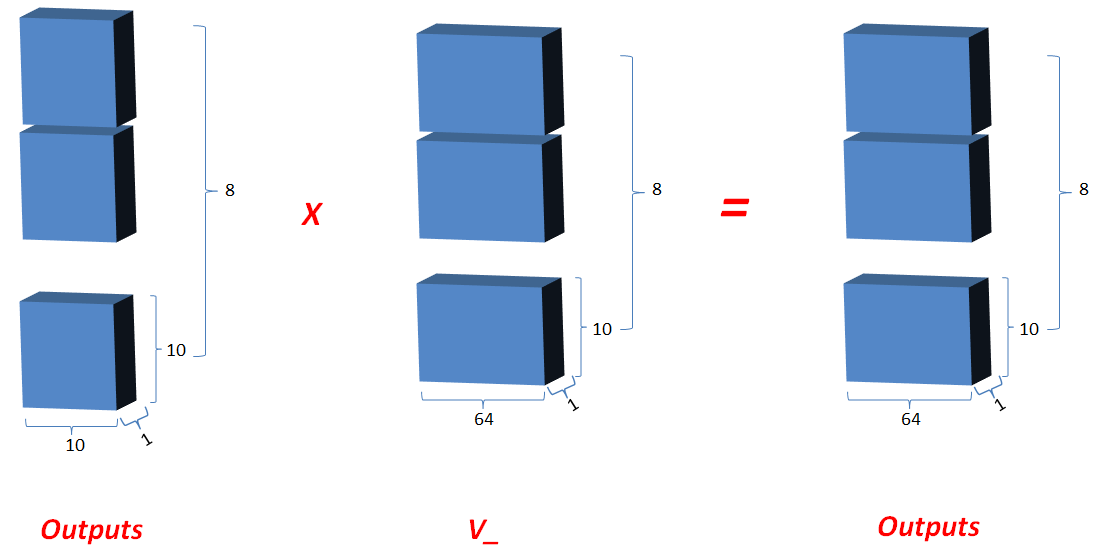
3.2.7 最后将outputs在axis=0维上切分为num_heads段，然后在axis=2维上合并， 恢复原来Q的维度；

 

 

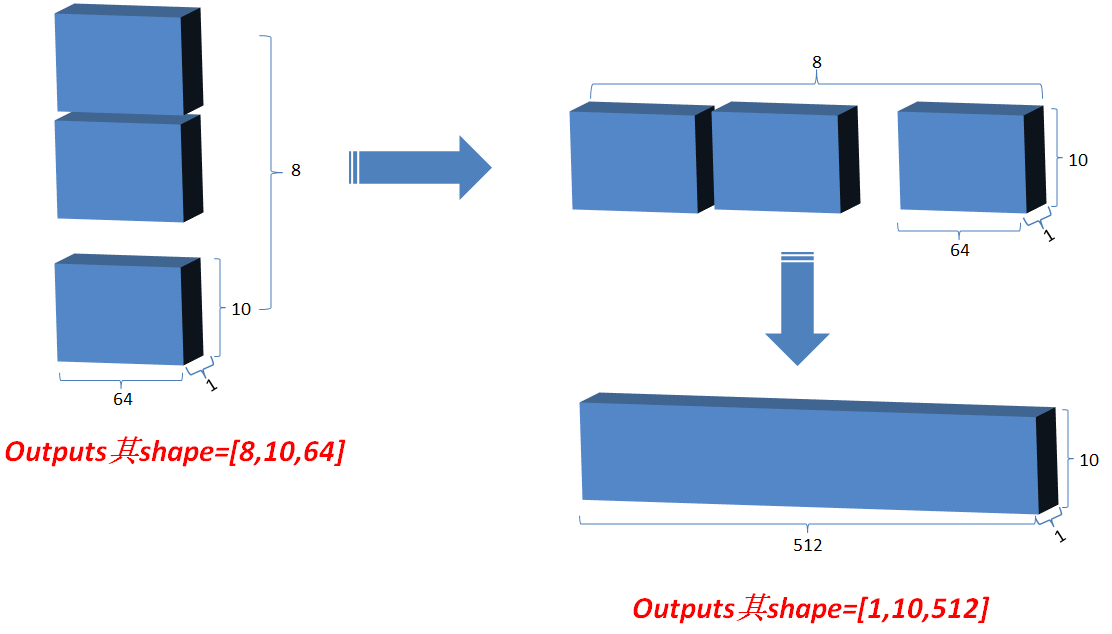
3.3 Add&norm

3.3.1 类似ResNet，将最初的输入与其对应的输出叠加一次，即outputs=outputs+Q， 使网络有效叠加，避免梯度消失；

 

 

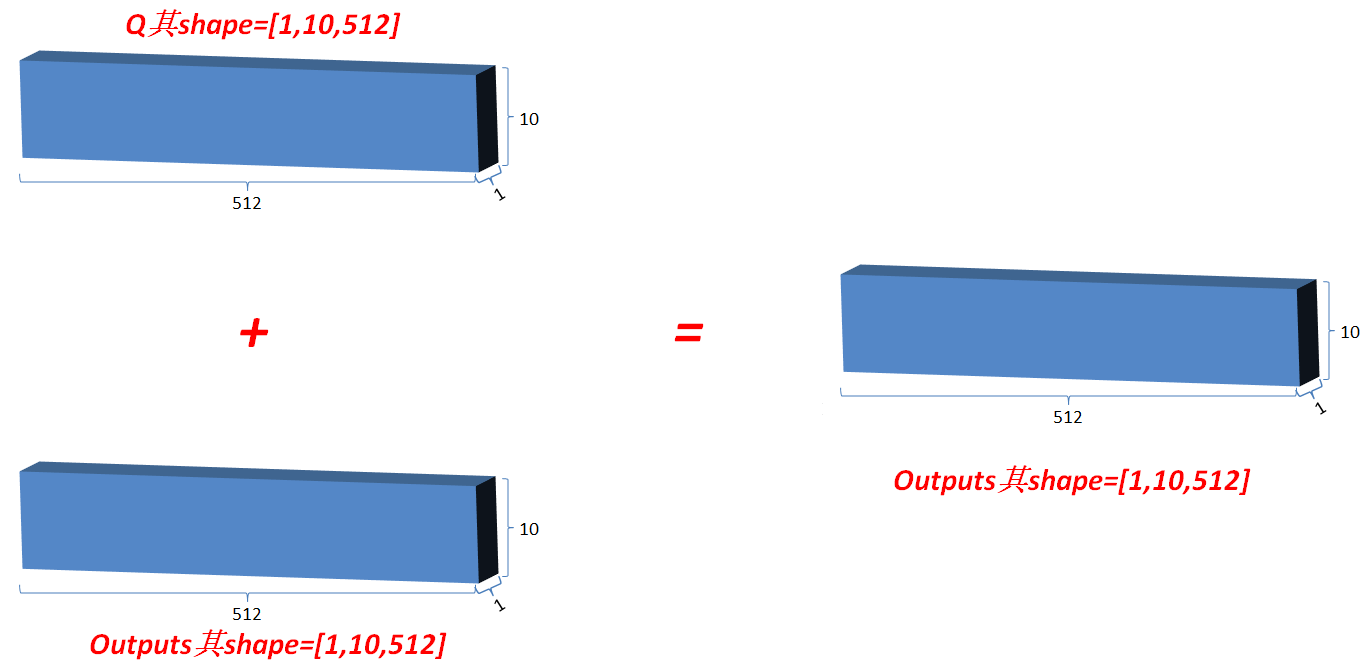
3.3.2 标准化矫正一次，在outputs对最后一维计算均值和方差，用outputs减去均值除以方差+spsilon得值更新为outputs，然后变量gamma*outputs+变量beta；

3.4 feedForward

3.4.1 对outputs进行第一次卷积操作，结果更新为outputs（卷积核为1*1，每一次卷积操作的计算发生在一个词对应的向量元素上，卷积核数目即最后一维向量长度，也就是一个词对应的向量维数）；

3.4.2 对最新outputs进行第二次卷积操作，卷积核仍然为1*1，卷积核数目为N；

 

 

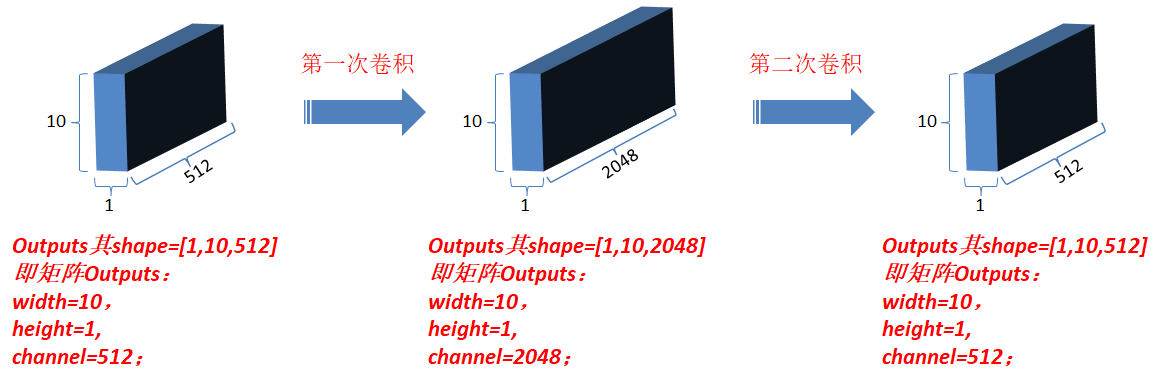
3.5 Add&norm : 和3.3相同，经过以上操作后，此时最新的output和matEnc的shape相同；

3.6 令matEnc=outputs, 完成一次循环，然后返回到3.2开始第二次循环；共循环Nx（自定义；每一次循环其结构相同，但对应的参数是不同的，即是独立训练的）；完成Nx次后，模型的编码部分完成，仍然令matEnc=outputs，准备进入解码部分；

 

解码部分：

1. Outputs：shifted right右移一位，是为了解码区最初初始化时第一次输入，并将其统一定义为特定值（在word2num中提前定义）；

2. Outputs embedding: 同编码部分；更新outputs；

3. Positional embedding：同编码部分；更新outputs；

4. 进入解码区循环体，即figure1中右侧红框内的部分；

4.1 Masked multi-head attention: 和编码部分的multi-head attention类似，但是多了一 次masked，因为在解码部分，解码的时候时从左到右依次解码的，当解出第一个字的时候，第一个字只能与第一个字计算相关性，当解出第二个字的时候，只能计算出第二个字与第一个字和第二个字的相关性，。。。；所以需要linalg.LinearOperatorLowerTriangular进行一次mask；

 

 

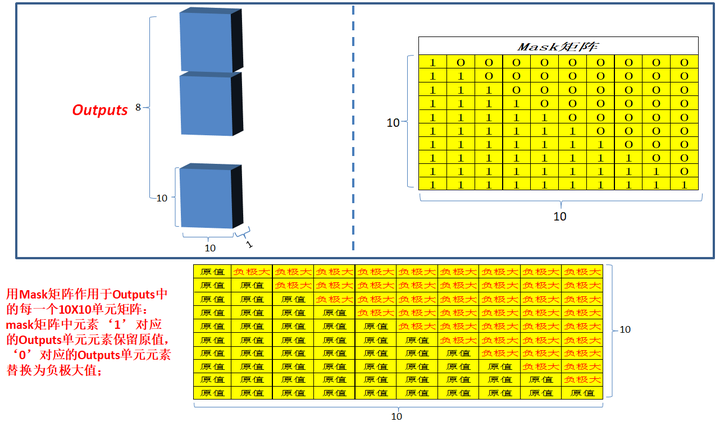
4.2 Add&norm：同编码部分，更新outputs；

4.3 Multi-head attention：同编码部分，但是Q和K，V不再相同，Q=outputs，K=V=matEnc；

4.4 Add&norm:同编码部分，更新outputs；

4.5 Feed-Forward：同编码部分，更新outputs；

4.6 Add&norm: 同编码部分，更新outputs；

4.7 最新outputs和最开始进入该循环时候的outputs的shape相同；回到4.1，开始第 二次循环。。。；直到完成Nx次循环（自定义；每一次循环其结构相同，但对应的参数是不同的，即独立训练的）；

5. Linear: 将最新的outputs，输入到单层神经网络中，输出层维度为“译文”有效单词总数；更新outputs；

6. Softmax: 对outputs进行softmax运算，确定模型译文和原译文比较计算loss，进行网络优化；