[转] 交叉熵 again
经典概念总是值得反复学习
from：https://zhuanlan.zhihu.com/p/61944055
1. 引言
我们都知道损失函数有很多种：均方误差（MSE）、SVM的合页损失（hinge loss）、交叉熵（cross entropy）。这几天看论文的时候产生了疑问：为啥损失函数很多用的都是交叉熵（cross entropy）？其背后深层的含义是什么？如果换做均方误差（MSE）会怎么样？下面我们一步步来揭开交叉熵的神秘面纱。
2. 交叉熵的来源
2.1 信息量
一条信息的信息量大小和它的不确定性有很大的关系。一句话如果需要很多外部信息才能确定，我们就称这句话的信息量比较大。比如你听到“云南西双版纳下雪了”，那你需要去看天气预报、问当地人等等查证（因为云南西双版纳从没下过雪）。相反，如果和你说“人一天要吃三顿饭”，那这条信息的信息量就很小，因为条信息的确定性很高。
那我们就能将事件x_0的信息量定义如下（其中p(x_0)表示事件x_0发生的概率）：
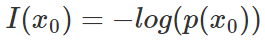
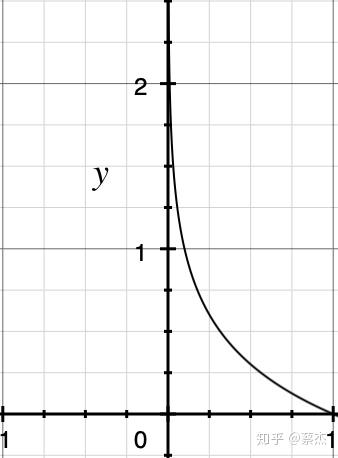概率总是一个0-1之间的值，-log(x)的图像如上
2.2 熵
信息量是对于单个事件来说的，但是实际情况一件事有很多种发生的可能，比如掷骰子有可能出现6种情况，明天的天气可能晴、多云或者下雨等等。熵是表示随机变量不确定的度量，是对所有可能发生的事件产生的信息量的期望。公式如下：
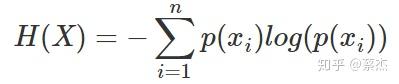n表示事件可能发生的情况总数
其中一种比较特殊的情况就是掷硬币，只有正、反两种情况，该种情况（二项分布或者0-1分布）熵的计算可以简化如下：
p(x)代表掷正面的概率，1-p(x)则表示掷反面的概率（反之亦然）
2.3 相对熵
相对熵又称KL散度，用于衡量对于同一个随机变量x的两个分布p(x)和q(x)之间的差异。在机器学习中，p(x)常用于描述样本的真实分布，例如[1,0,0,0]表示样本属于第一类，而q(x)则常常用于表示预测的分布，例如[0.7,0.1,0.1,0.1]。显然使用q(x)来描述样本不如p(x)准确，q(x)需要不断地学习来拟合准确的分布p(x)。
KL散度的公式如下：
n表示事件可能发生的情况总数
KL散度的值越小表示两个分布越接近。
2.4 交叉熵
我们将KL散度的公式进行变形，得到：
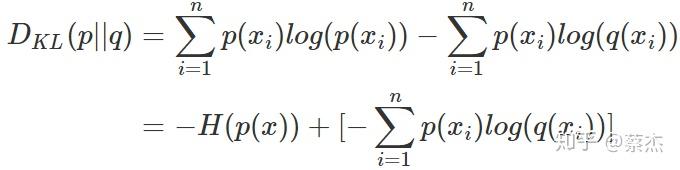
前半部分就是p(x)的熵，后半部分就是我们的交叉熵：
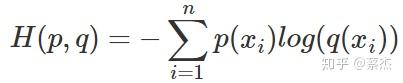
机器学习中，我们常常使用KL散度来评估predict和label之间的差别，但是由于KL散度的前半部分是一个常量，所以我们常常将后半部分的交叉熵作为损失函数，其实二者是一样的。
3. 交叉熵作为loss函数的直觉
在回归问题中，我们常常使用均方误差（MSE）作为损失函数，其公式如下：
m表示样本个数，loss表示的是m个样本的均值
其实这里也比较好理解，因为回归问题要求拟合实际的值，通过MSE衡量预测值和实际值之间的误差，可以通过梯度下降的方法来优化。而不像分类问题，需要一系列的激活函数（sigmoid、softmax）来将预测值映射到0-1之间，这时候再使用MSE的时候就要好好掂量一下了，为啥这么说，请继续看：
sigmoid加MES的基本公式
gradient推导过程
上面复杂的推导过程，其实结论就是下面一张图：
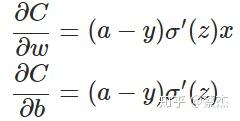C就是 的J，sigma就是sigmoid函数，a就是predict
从以上公式可以看出，w和b的梯度跟激活函数的梯度成正比，激活函数的梯度越大，w和b的大小调整得越快，训练收敛得就越快。而我们都知道sigmoid函数长这样：
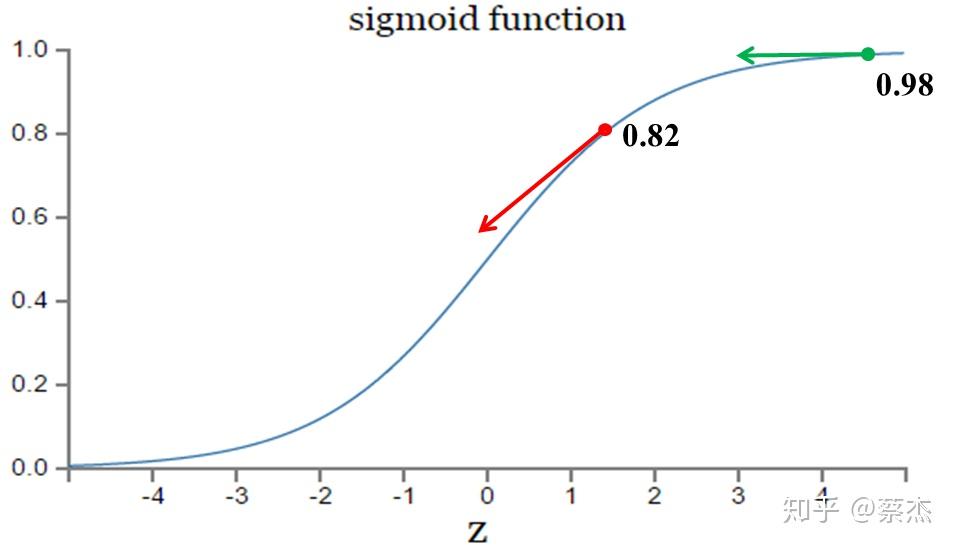图片来自：https://blog.csdn.net/u014313009/article/details/51043064
在上图的绿色部分，初始值是0.98，红色部分初始值是0.82，假如真实值是0。直观来看那么0.82下降的速度明显高于0.98，但是明明0.98的误差更大，这就导致了神经网络不能像人一样，误差越大，学习的越快。
但是如果我们把MSE换成交叉熵会怎么样呢？
x表示样本，n表示样本的总数
重新计算梯度：
推导过程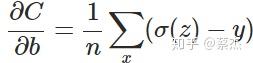
另外sigmoid有一个很好的性质：
我们从结果可以看出梯度中不再含有sigmoid的导数，有的是sigmoid的值和实际值之间的差，也就满足了我们之前所说的错误越大，下降的越快。
这也就是在分类问题中常用cross entropy 而不是 MSE的原因了。
