[转] 似然函数与概率
知乎还是明白人多啊,讲明白儿的
from:https://www.zhihu.com/question/54082000
链接:https://www.zhihu.com/question/54082000/answer/145495695
来源:知乎
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
We must return to the actual fact that one value of, of the frequency of which we know nothing, would yield the observed result three times as frequently as would another value of
. If we need a word to characterize this relative property of different values of
, I suggest that we may speak without confusion of the
of one value of
being thrice the likelihood of another, bearing always in mind that likelihood is not here used loosely as a synonym of probability, but simply to express the relative frequencies with which such values of the hypothetical quantity
would in fact yield the observed sample.
除此之外,统计学中的另一常见概念"置信(区间)"(confidence interval)中的置信度(confidence level) 或者称为置信系数 (confidence coefficient) 也不是概率。换句话说,"构建关于总体均值的95%的置信区间"里的"95%"不是概率意义下的0.95(即使它也是0到1之间的代表机会chance的一个度量): Neyman的原话是
... in the long run he will be correct in 99% (the assumed value of) of all cases ... Hence the frequency of actually correct statements will approach
![[公式]](https://www.zhihu.com/equation?tex=%5Calpha)
更常见的 -值(
-value)严格来说其本身是一个(恰好位于0到1之间的)统计量(即样本随机变量的函数),所以
-值也不是概率。
一种方便区别是概率还是似然的方法是,根据定义,"谁谁谁的概率"中谁谁谁只能是概率空间中的事件,换句话说,我们只能说,事件(发生)的概率是多少多少(因为事件具有概率结构从而刻画随机性,所以才能谈概率);而"谁谁谁的似然"中的谁谁谁只能是参数,比如说,参数等于 时的似然是多少。
2、似然与概率的联系
先看似然函数的定义,它是给定联合样本值下关于(未知)参数
的函数:
这里的小是指联合样本随机变量
取到的值,即
;
这里的是指未知参数,它属于参数空间;
这里的是一个密度函数,特别地,它表示(给定)
下关于联合样本值
的联合密度函数。
所以从定义上,似然函数和密度函数是完全不同的两个数学对象:前者是关于的函数,后者是关于
的函数。所以这里的等号
理解为函数值形式的相等,而不是两个函数本身是同一函数(根据函数相等的定义,函数相等当且仅当定义域相等并且对应关系相等)。
说完两者的区别,再说两者的联系。
(1)如果是离散的随机向量,那么其概率密度函数
可改写为
,即代表了在参数
下随机向量
取到值
的可能性;并且,如果我们发现
那么似然函数就反应出这样一个朴素推测:在参数下随机向量
取到值
的可能性大于 在参数
下随机向量
取到值
的可能性。换句话说,我们更有理由相信(相对于
来说)
更有可能是真实值。这里的可能性由概率来刻画。
(2)如果是连续的随机向量,那么其密度函数
本身(如果在
连续的话)在
处的概率为0,为了方便考虑一维情况:给定一个充分小
,那么随机变量
取值在
区间内的概率即为
并且两个未知参数的情况下做比就能约掉,所以和离散情况下的理解一致,只是此时似然所表达的那种可能性和概率
无关。
综上,概率(密度)表达给定下样本随机向量
的可能性,而似然表达了给定样本
下参数
(相对于另外的参数
)为真实值的可能性。我们总是对随机变量的取值谈概率,而在非贝叶斯统计的角度下,参数是一个实数而非随机变量,所以我们一般不谈一个参数的概率。
最后我们再回到这个表达。首先我们严格记号,竖线
表示条件概率或者条件分布,分号
表示把参数隔开。所以这个式子的严格书写方式是
因为
在右端只当作参数理解。
分享
这个是quora上的一个回答 What is the difference between probability and likelihood?
在评论中这位老师将概率密度函数和似然函数之间的关系,类比成 和
之间的关系。详细翻译如下:
2我们可以做一个类比,假设一个函数为 ,这个函数包含两个变量。
如果你令b=2,这样你就得到了一个关于a的二次函数,即 :
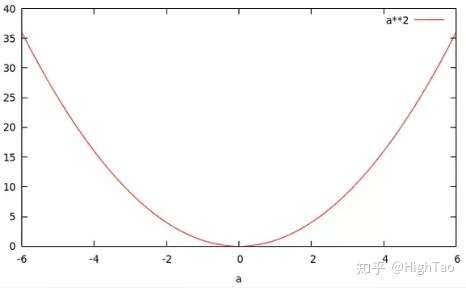
当你令a=2时,你将得到一个关于b的指数函数,即 :
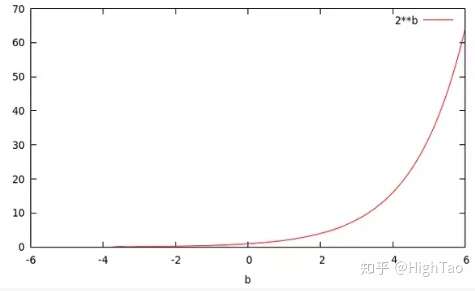
可以看到这两个函数有着不同的名字,却源于同一个函数。
而p(x|θ)也是一个有着两个变量的函数。如果,你将θ设为常量,则你会得到一个概率函数(关于x的函数);如果,你将x设为常量你将得到似然函数(关于θ的函数)。
下面举一个例子:
有一个硬币,它有θ的概率会正面向上,有1-θ的概率反面向上。θ是存在的,但是你不知道它是多少。为了获得θ的值,你做了一个实验:将硬币抛10次,得到了一个正反序列:x=HHTTHTHHHH。
无论θ的值是多少,这个序列的概率值为 θ⋅θ⋅(1-θ)⋅(1-θ)⋅θ⋅(1-θ)⋅θ⋅θ⋅θ⋅θ = θ⁷ (1-θ)³
比如,如果θ值为0,则得到这个序列的概率值为0。如果θ值为1/2,概率值为1/1024。
但是,我们应该得到一个更大的概率值,所以我们尝试了所有θ可取的值,画出了下图:
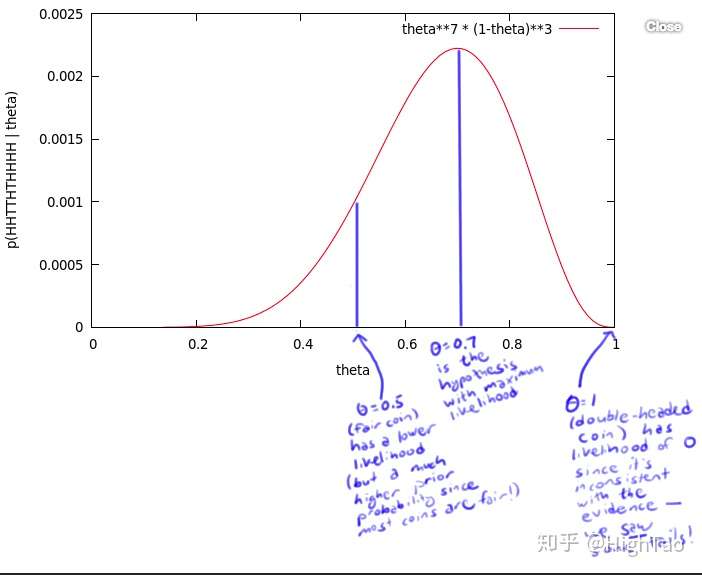
这个曲线就是θ的似然函数,通过了解在某一假设下,已知数据发生的可能性,来评价哪一个假设更接近θ的真实值。
如图所示,最有可能的假设是在θ=0.7的时候取到。但是,你无须得出最终的结论θ=0.7。事实上,根据贝叶斯法则,0.7是一个不太可能的取值(如果你知道几乎所有的硬币都是均质的,那么这个实验并没有提供足够的证据来说服你,它是均质的)。但是,0.7却是最大似然估计的取值。
因为这里仅仅试验了一次,得到的样本太少,所以最终求出的最大似然值偏差较大,如果经过多次试验,扩充样本空间,则最终求得的最大似然估计将接近真实值0.5。在这篇博客中有详细的过程,就不再赘述。



