[转] 残差网络
from : https://zhuanlan.zhihu.com/p/22447440
Revisiting Deep Convolution Network
2012年，计算机视觉界顶级比赛ILSVRC中，多伦多大学Hinton团队所提出的深度卷积神经网络结构AlexNet[1]一鸣惊人，同时也拉开了深度卷积神经网络在计算机视觉领域广泛应用的序幕，如图1所示。
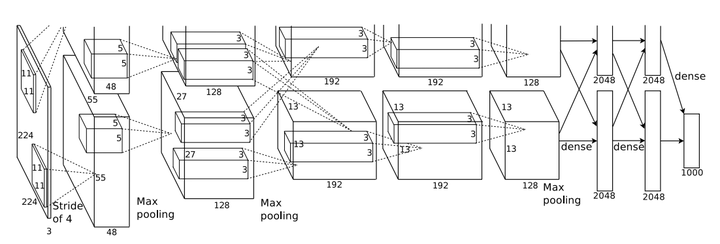
图1 AlexNet网络结构
2014年，Google公司的GoogleNet[2]和牛津大学视觉几何组的VGGNet[3]在当年的ILSVRC中再一次各自使用深度卷积神经网络取得了优异的成绩，并在分类错误率上优于AlexNet数个百分点，再一次将深度卷积神经网络推上了新的巅峰。两种结构相较于AlexNet，继续选择了增加网络复杂程度的策略来增强网络的特征表示能力。 2015年，微软亚洲研究院的何凯明等人使用残差网络ResNet[4]参加了当年的ILSVRC，在图像分类、目标检测等任务中的表现大幅超越前一年的比赛的性能水准，并最终取得冠军。残差网络的明显特征是有着相当深的深度，从32层到152层，其深度远远超过了之前提出的深度网络结构，而后又针对小数据设计了1001层的网络结构。残差网络ResNet的深度惊人，极其深的深度使该网络拥有极强大的表达能力。本文剩余部分将对残差网络及其变种进行详细的介绍。
Deeper is better?
上一部分我们回顾了深度卷积神经网络的发展历程，可以明显发现，网络的表达能力是随着网络深度的增加而增强的。何恺明等人的实验[5]也证明，时间复杂度相同的两种网络结构，深度较深的网络性能会有相对的提升。 然而，网络并非越深越好。抛开计算代价的问题不谈，在网络深度较深时，继续增加层数并不能提高性能，如图2所示。可以看到，在“平整”网络(与本文所介绍的残差网络复杂程度相同，但未使用残差结构的网络)中，随着网络层数的增加，其性能不但没有提升，反而出现了显著的退化。由于训练误差也随着层数增加而提升，所以这个现象可能并非参数的增加造成的过拟合；此外，这个网络在训练时也使用了ReLU激活、BN等手段，一定程度上缓解了梯度消失，这个现象可能也并非完全由梯度消失造成的。这个问题仍有待理论层面的研究和解决。 那么当下真的没有办法让网络更深了吗？把思路打开，假设上面的实验场景中，多增加的26层全部为单位映射，那么完全可以认为不会产生性能的损失。当然实际应用中这样做是没有意义的，但如果增加的层可以近似为单位映射，或者增加了些许扰动的单位映射，那么就有可能实现上述假设。在这一思路的引导下，深度残差学习(Deep Residual Learning)应运而生。
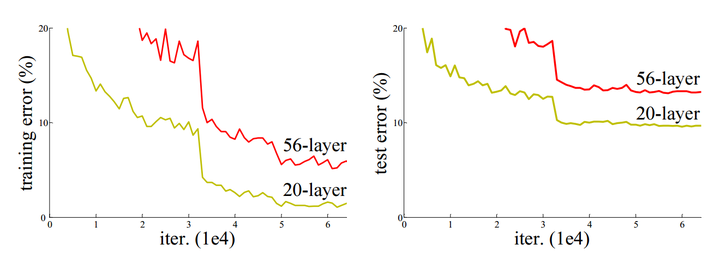
图2 使用Cifar-10数据集对“平整”网络进行训练和测试对应的误差
Deep Residual Learning
（2）初始化：
我们设深度网络中某隐含层为H（x）-x→F（x），如果可以假设多个非线性层组合可以近似于一个复杂函数，那么也同样可以假设隐含层的残差近似于某个复杂函数[6]。即那么我们可以将隐含层表示为H（x）=F（x）+ x。
这样一来，我们就可以得到一种全新的残差结构单元，如图3所示。可以看到，残差单元的输出由多个卷积层级联的输出和输入元素间相加(保证卷积层输出和输入元素维度相同)，再经过ReLU激活后得到。将这种结构级联起来，就得到了残差网络。典型网络结构表1所示。
图3 残差单元示意图可以注意到残差网络有这样几个特点：1. 网络较瘦，控制了参数数量；2. 存在明显层级，特征图个数逐层递进，保证输出特征表达能力；3. 使用了较少的池化层，大量使用下采样，提高传播效率；4. 没有使用Dropout，利用BN和全局平均池化进行正则化，加快了训练速度；5. 层数较高时减少了3x3卷积个数，并用1x1卷积控制了3x3卷积的输入输出特征图数量，称这种结构为“瓶颈”(bottleneck)。
表1 典型的残差网络结构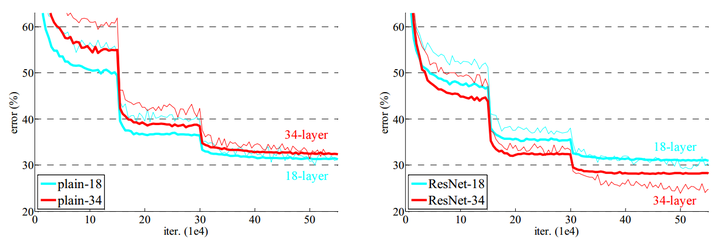
图4 ImageNet数据集上“平整”网络和残差网络的收敛性能
图5 ImageNet数据集上残差网络和其他网络单模型分类验证错误率对比 (VGG对应值为测试误差)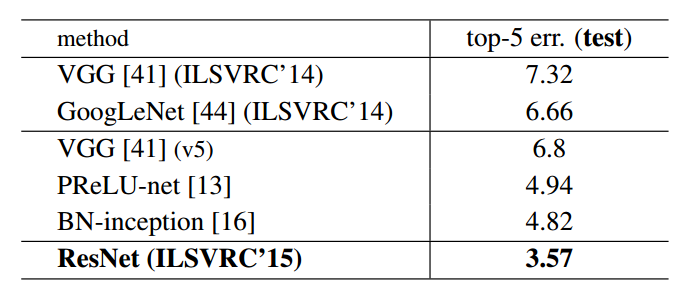
图6 ImageNet数据集上残差网络和其他网络集成模型分类测试错误率对比
图7 在Cifar-10数据集上网络各层响应的方差分布 上图：按照原网络层数排列；下图：按照方差大小排列收敛性能：图4中可以看到，与之前的实验不同，残差网络增加了一定层数之后，并未出现性能退化，反而性能有了一定程度的提升：残差网络有着更低的收敛损失，同时也没有产生过高的过拟合。同时注意到，残差网络在浅层时并未表现出更多的优势，说明残差网络必须要配合较深的深度才能发挥其结构优势，与“平整”网络拉开性能差距。
分类性能：图5和图6是几种网络结构在ImageNet数据集上单模型及集成模型分类错误率的对比。可以发现，残差网络系由于层数普遍高于以上模型，且又有残差结构作为极深度的支持前提，使得其性能普遍高于此前的各类优秀模型。此外，残差网络的性能也确实如期望随着网络层数的提升而提升。在100层以上时已经远远甩开了IRSVRC 2014的冠亚军网络模型。
网络响应：图7中可以看出，残差网络中大部分层的响应方差都处在较低水平，这一定程度上印证了我们的假设：这些响应方差较低的层响应较为固定，很有可能权重近似于零，这也就是说其所对应的残差结构可能近似于单位映射,网络的实际有效层数是要比全部层数要少一些的，产生了跳过连接(Skip-connection)的作用。这样也就是网络为什么在较深的深度下仍可以保持并提升性能，且没有过多增加训练难度的原因。
ResDeeper more
何恺明等人基于深度残差结构，进一步设计了一些其他的残差网络模型，用于Cifar-10数据集上的分类任务，分类错误率如图8所示。可以看到，110层以下的残差网络中均表现出了较强的分类性能。但在使用1202层残差网络模型时，分类性能出现了退化，甚至不如32层残差网络的表现。由于Cifar-10数据集尺寸和规模相对较小，此处1202层模型也并未使用Dropout等强正则化手段，1202层的网络有可能已经产生过拟合，但也不能排除和之前“平整”网络情况类似的原因导致的性能退化。
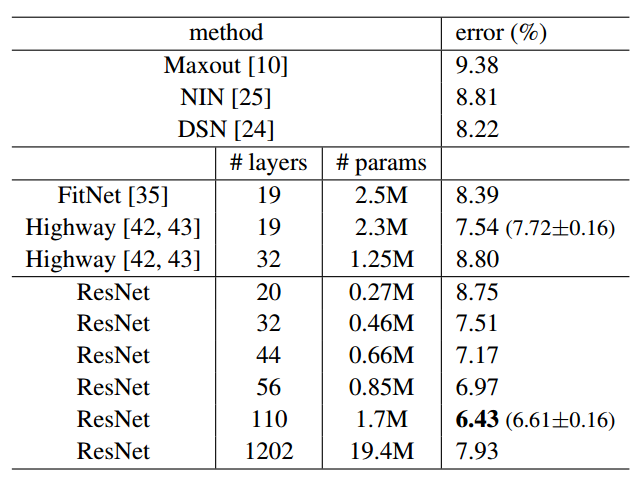图8 Cifar-10数据集上残差网络和其他网络分类测试错误率对比何恺明等人经过一段时间的研究，认为极其深的深度网络可能深受梯度消失问题的困扰，BN、ReLU等手段对于这种程度的梯度消失缓解能力有限，并提出了单位映射的残差结构[7]。这种结构从本源上杜绝了梯度消失的问题：
基于反向传播法计算梯度优化的神经网络，由于反向传播求隐藏层梯度时利用了链式法则，梯度值会进行一系列的连乘，导致浅层隐藏层的梯度会出现剧烈的衰减，这也就是梯度消失问题的本源，这种问题对于Sigmoid激活尤为严重，故后来深度网络均使用ReLU激活来缓解这个问题，但即使是ReLU激活也无法避免由于网络单元本身输出的尺度关系，在极深度条件下成百上千次的连乘带来的梯度消失。
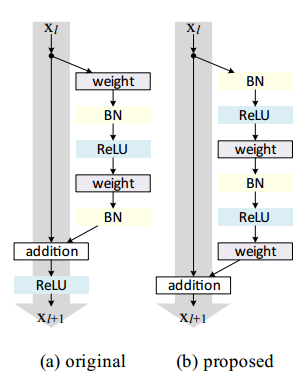
图9 原始残差单元和预激活残差单元的对比
实验证明，将激活层融合到残差支路中，并使用ReLU预激活的残差单元，不仅可以满足之前的假设，并且实验证明在各种已知的结构里面也是最优的[7]，预激活单元和原始残差单元的示意图如图9所示。可以看到，预激活的残差单元在残差支路中进行每次卷积之前即完成激活，然后再进行矩阵元素间加法进行合并，既满足了激活要求，也使得支路外不再需要额外激活。
图10 Cifar-10数据集上训练1001层残差网络的训练曲线
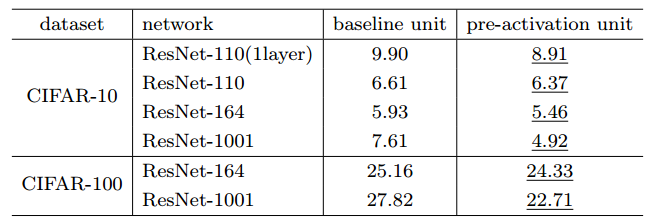图11 Cifar-10和Cifar-100数据集上各种残差网络 使用不同残差单元的分类测试误差对比使用预激活残差单元构筑的残差网络收敛性能和分类性能分别如图10和图11所示。可以看到，使用预激活残差单元，相较于使用原始单元更易收敛，且有一定正则化的效果，测试集上性能也普遍好于原始残差单元。
Conclusion
残差网络结构简单，解决了极深度条件下深度卷积神经网络性能退化的问题，分类性能表现出色。从ILSVRC 2015至今半年多的时间里，残差网络的广泛使用已推进计算机视觉各任务的性能升入新的高度。
残差网络表现出的良好图像分类性能，同样也可以进一步推广到人脸识别领域上来。使用残差网络，可以大幅提升人脸分类性能。在人脸识别准确率每3个月提升一个数量级的今天，残差网络及未来更高性能的网络结构必定会将这个周期进一步的缩短。
Reference
[1]Krizhevsky, Alex, Ilya Sutskever, and Geoffrey E. Hinton. "Imagenet classification with deep convolutional neural networks." Advances in neural information processing systems. 2012.
[2]Szegedy, Christian, et al. "Going deeper with convolutions." Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. 2015.
[3]Simonyan, Karen, and Andrew Zisserman. "Very deep convolutional networks for large-scale image recognition." arXiv preprint arXiv:1409.1556(2014).
[4]He, Kaiming, et al. "Deep residual learning for image recognition." arXiv preprint arXiv:1512.03385 (2015).
[5]He, Kaiming, and Jian Sun. "Convolutional neural networks at constrained time cost." Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. 2015.
[6]Montufar, Guido F., et al. "On the number of linear regions of deep neural networks." Advances in neural information processing systems. 2014.[7]He, Kaiming, et al. "Identity mappings in deep residual networks." arXiv preprint arXiv:1603.05027 (2016).
