[转] 理解各种熵&&最大熵模型

把各种熵的好文集中一下，希望面试少受点伤，哈哈哈

1. 条件熵 https://zhuanlan.zhihu.com/p/26551798

我们首先知道信息熵是考虑该随机变量的所有可能取值，即所有可能发生事件所带来的信息量的期望。公式如下：

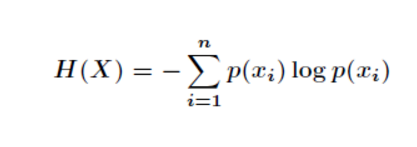我们的条件熵的定义是：定义为X给定条件下，Y的条件概率分布的熵对X的数学期望

这个还是比较抽象，下面我们解释一下：

设有随机变量（X,Y），其联合概率分布为

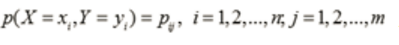条件熵H（Y|X）表示在已知随机变量X的条件下随机变量Y的不确定性。随机变量X给定的条件下随机变量Y的条件熵H(Y|X)

公式

下面推导一下条件熵的公式：

注意

注意，这个条件熵，不是指在给定某个数（某个变量为某个值）的情况下，另一个变量的熵是多少，变量的不确定性是多少？

因为条件熵中X也是一个变量，意思是在一个变量X的条件下（变量X的每个值都会取），另一个变量Y熵对X的期望。

这是最容易错的！

例子

下面通过例子来解释一下：

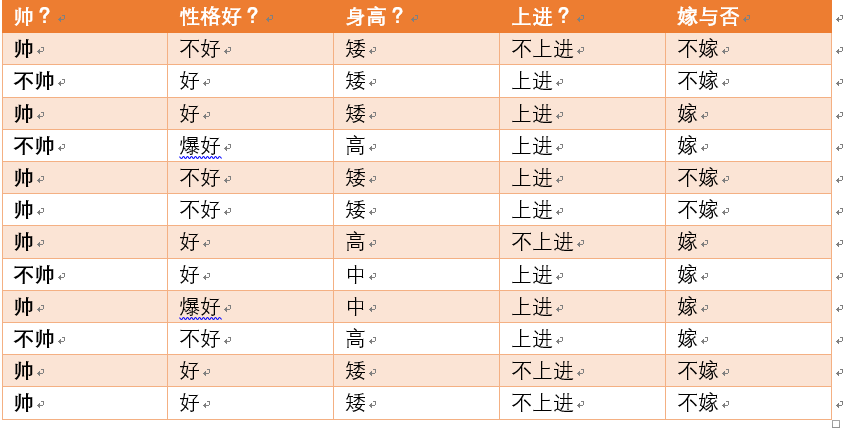
假如我们有上面数据：

设随机变量Y={嫁，不嫁}

我们可以统计出，嫁的个数为6/12 = 1/2

不嫁的个数为6/12 = 1/2

那么Y的熵，根据熵的公式来算，可以得到H（Y） = -1/2log1/2 -1/2log1/2

为了引出条件熵，我们现在还有一个变量X，代表长相是帅还是帅，当长相是不帅的时候，统计如下红色所示：

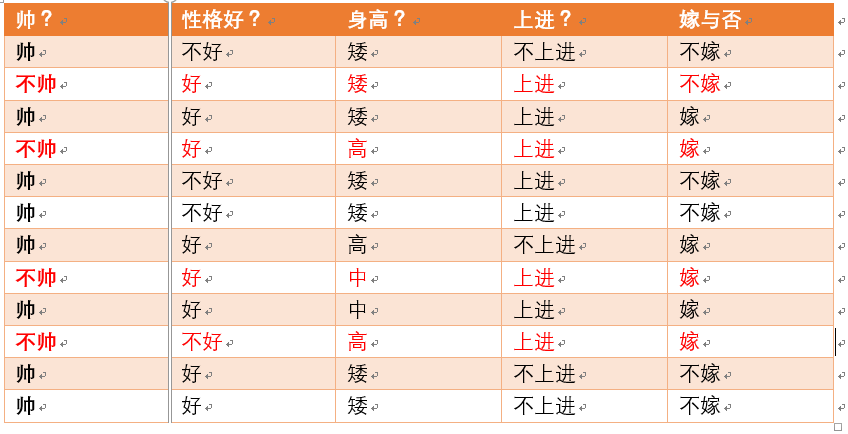
可以得出，当已知不帅的条件下，满足条件的只有4个数据了，这四个数据中，不嫁的个数为1个，占1/4

嫁的个数为3个，占3/4

那么此时的H（Y|X = 不帅） = -1/4log1/4-3/4log3/4

p(X = 不帅) = 4/12 = 1/3

同理我们可以得到：

当已知帅的条件下，满足条件的有8个数据了，这八个数据中，不嫁的个数为5个，占5/8

嫁的个数为3个，占3/8

那么此时的H（Y|X = 帅） = -5/8log5/8-3/8log3/8

p(X = 帅) = 8/12 = 2/3

计算结果

有了上面的铺垫之后，我们终于可以计算我们的条件熵了，我们现在需要求：

H（Y|X = 长相）

也就是说，我们想要求出当已知长相的条件下的条件熵。

根据公式我们可以知道，长相可以取帅与不帅俩种

条件熵是另一个变量Y熵对X（条件）的期望。

公式为：

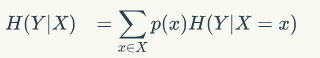
H（Y|X=长相） = p(X =帅)*H（Y|X=帅）+p(X =不帅)*H（Y|X=不帅）

然后将上面已经求得的答案带入即可求出条件熵！

这里比较容易错误就是忽略了X也是可以取多个值，然后对其求期望！！

总结

其实条件熵意思是按一个新的变量的每个值对原变量进行分类，比如上面这个题把嫁与不嫁按帅，不帅分成了俩类。

然后在每一个小类里面，都计算一个小熵，然后每一个小熵乘以各个类别的概率，然后求和。

我们用另一个变量对原变量分类后，原变量的不确定性就会减小了，因为新增了Y的信息，可以感受一下。不确定程度减少了多少就是信息的增益。

后面会讲信息增益的概念，信息增益也是决策树算法的关键。

－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－

2. 各种熵

from: https://zhuanlan.zhihu.com/p/35379531

信息熵
条件熵
相对熵
交叉熵
总结

一信息熵 (information entropy)

熵 (entropy) 这一词最初来源于热力学。1948年，克劳德·爱尔伍德·香农将热力学中的熵引入信息论，所以也被称为香农熵 (Shannon entropy)，信息熵 (information entropy)。本文只讨论信息熵。首先，我们先来理解一下信息这个概念。信息是一个很抽象的概念，百度百科将它定义为：指音讯、消息、通讯系统传输和处理的对象，泛指人类社会传播的一切内容。那信息可以被量化么？可以的！香农提出的“信息熵”概念解决了这一问题。

一条信息的信息量大小和它的不确定性有直接的关系。我们需要搞清楚一件非常非常不确定的事，或者是我们一无所知的事，就需要了解大量的信息。相反，如果我们对某件事已经有了较多的了解，我们就不需要太多的信息就能把它搞清楚。所以，从这个角度，我们可以认为，信息量的度量就等于不确定性的多少。比如，有人说广东下雪了。对于这句话，我们是十分不确定的。因为广东几十年来下雪的次数寥寥无几。为了搞清楚，我们就要去看天气预报，新闻，询问在广东的朋友，而这就需要大量的信息，信息熵很高。再比如，中国男足进军2022年卡塔尔世界杯决赛圈。对于这句话，因为确定性很高，几乎不需要引入信息，信息熵很低。

考虑一个离散的随机变量 x，由上面两个例子可知，信息的量度应该依赖于概率分布 p(x)，因此我们想要寻找一个函数 I(x)，它是概率 p(x) 的单调函数，表达了信息的内容。怎么寻找呢？如果我们有两个不相关的事件 x和 y，那么观察两个事件同时发生时获得的信息量应该等于观察到事件各自发生时获得的信息之和，即：I(x,y)=I(x)+I(y)。

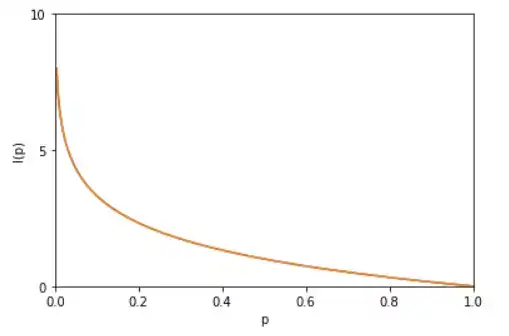
因为两个事件是独立不相关的，因此 p(x,y)=p(x)p(y)。根据这两个关系，很容易看出 I(x)一定与 p(x) 的对数有关 (因为对数的运算法则是 loga(mn)=logam+logan因此，我们有I(x)=−logp(x)。其中负号是用来保证信息量是正数或者零。而 log函数基的选择是任意的（信息论中基常常选择为2，因此信息的单位为比特bits；而机器学习中基常常选择为自然常数，因此单位常常被称为奈特nats）。I(x)也被称为随机变量 x的自信息 (self-information)，描述的是随机变量的某个事件发生所带来的信息量。图像如图：

最后，我们正式引出信息熵。现在假设一个发送者想传送一个随机变量的值给接收者。那么在这个过程中，他们传输的平均信息量可以通过求 I(x)=−logp(x)关于概率分布 p(x) 的期望得到，即：

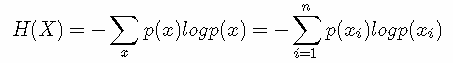
H(X) 就被称为随机变量 x的熵,它是表示随机变量不确定的度量，是对所有可能发生的事件产生的信息量的期望。从公式可得，随机变量的取值个数越多，状态数也就越多，信息熵就越大，混乱程度就越大。当随机分布为均匀分布时，熵最大，且 0≤H(X)≤logn。稍后证明。将一维随机变量分布推广到多维随机变量分布，则其联合熵(Joint entropy) 为：

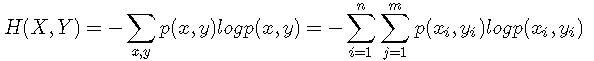
（注意：熵只依赖于随机变量的分布,与随机变量取值无关，所以也可以将 X的熵记作 H(p)；令0log0=0(因为某个取值概率可能为0)）

那么这些定义有着什么样的性质呢？考虑一个随机变量 x。这个随机变量有4种可能的状态，每个状态都是等可能的。为了把 x 的值传给接收者，我们需要传输2比特的消息。H(X)=−4×(1/4)log2(1/4)=2 bits。现在考虑一个具有4种可能的状态 {a,b,c,d} 的随机变量，每个状态各自的概率为 (1/2,1/4,1/8,1/8)。这种情形下的熵为：

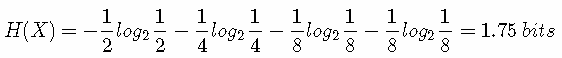
我们可以看到，非均匀分布比均匀分布的熵要小。现在让我们考虑如何把变量状态的类别传递给接收者。与之前一样，我们可以使用一个2比特的数字来完成这件事情。然而，我们可以利用非均匀分布这个特点，使用更短的编码来描述更可能的事件，使用更长的编码来描述不太可能的事件。我们希望这样做能够得到一个更短的平均编码长度。我们可以使用下面的编码串（哈夫曼编码）：0、10、110、111来表示状态 {a,b,c,d}。传输的编码的平均长度就是：

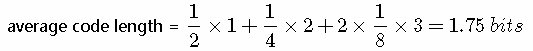
这个值与上方的随机变量的熵相等。熵和最短编码长度的这种关系是一种普遍的情形。Shannon 编码定理表明熵是传输一个随机变量状态值所需的比特位下界（最短平均编码长度）。因此，信息熵可以应用在数据压缩方面。可参考这篇文章讲的很详细了，我就不赘述了。（http://www.ruanyifeng.com/blog/2014/09/information-entropy.html）

证明0≤H(X)≤logn 利用拉格朗日乘子法证明： 因为 p(1)+p(2)+⋯+p(n)=1 所以有： 目标函数：f(p(1),p(2),…,p(n))=−(p(1)logp(1)+p(2)logp(2)+⋯+p(n)logp(n)) 约束条件：g(p(1),p(2),…,p(n),λ)=p(1)+p(2)+⋯+p(n)−1=0 1) 定义拉格朗日函数： L(p(1),p(2),…,p(n),λ)=−(p(1)logp(1)+p(2)logp(2)+⋯+p(n)logp(n))+λ(p(1)+p(2)+⋯+p(n)−1) 2) L(p(1),p(2),…,p(n),λ)分别对 p(1),p(2),p(n),λ求偏导数，令偏导数为 0： λ−log(e⋅p(1))=0 λ−log(e⋅p(2))=0 …………λ−log(e⋅p(n))=0 p(1)+p(2)+⋯+p(n)−1=0 3) 求出 p(1),p(2),…,p(n)值：解方程得，p(1)=p(2)=⋯=p(n)=1/n代入 f(p(1),p(2),…,p(n)) 中得到目标函数的极值为:

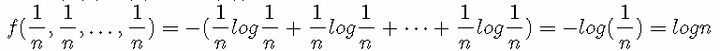
由此可证 logn为最大值。

二条件熵 (Conditional entropy)

条件熵 H(Y|X)表示在已知随机变量 X 的条件下随机变量 Y 的不确定性。条件熵 H(Y|X)定义为 X 给定条件下 Y 的条件概率分布的熵对 X 的数学期望：

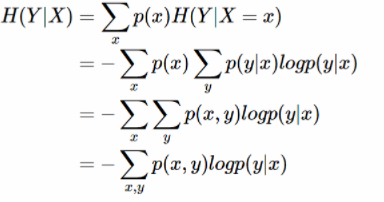
条件熵 H(Y|X)相当于联合熵 H(X,Y)减去单独的熵 H(X)，即H(Y|X)=H(X,Y)−H(X)，证明如下：

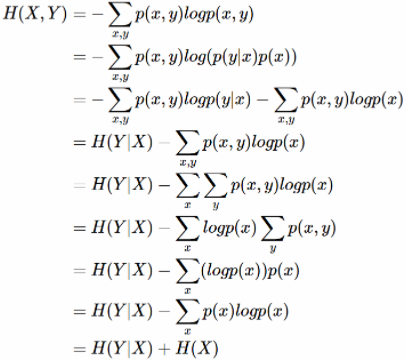
举个例子，比如环境温度是低还是高，和我穿短袖还是外套这两个事件可以组成联合概率分布 H(X,Y)，因为两个事件加起来的信息量肯定是大于单一事件的信息量的。假设 H(X)对应着今天环境温度的信息量，由于今天环境温度和今天我穿什么衣服这两个事件并不是独立分布的，所以在已知今天环境温度的情况下，我穿什么衣服的信息量或者说不确定性是被减少了。当已知 H(X) 这个信息量的时候，H(X,Y) 剩下的信息量就是条件熵：H(Y|X)=H(X,Y)−H(X)

因此，可以这样理解，描述 X 和 Y 所需的信息是描述 X 自己所需的信息,加上给定 X的条件下具体化 Y 所需的额外信息。关于条件熵的例子可以看这篇文章，讲得很详细。（https://zhuanlan.zhihu.com/p/26551798）

三相对熵 (Relative entropy)，也称KL散度 (Kullback–Leibler divergence)

设 p(x)、q(x) 是离散随机变量 X 中取值的两个概率分布，则 p 对 q 的相对熵是：

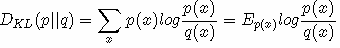
性质：

如果 p(x) 和 q(x) 两个分布相同，那么相对熵等于0
DKL(p||q)≠DKL(q||p)，相对熵具有不对称性。大家可以举个简单例子算一下。
DKL(p||q)≥0证明如下：(用Jensen不等式https://en.wikipedia.org/wiki/Jensen%27s_inequality)

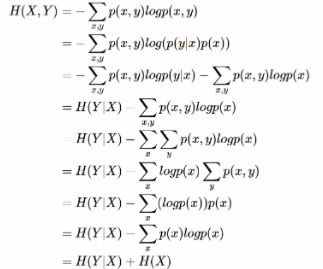
因为：

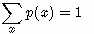
所以：

DKL(p||q)≥0

总结：相对熵可以用来衡量两个概率分布之间的差异，上面公式的意义就是求 p 与 q 之间的对数差在 p 上的期望值。

四交叉熵 (Cross entropy)

现在有关于样本集的两个概率分布 p(x) 和 q(x)，其中 p(x) 为真实分布， q(x)非真实分布。如果用真实分布 p(x) 来衡量识别一个样本所需要编码长度的期望（平均编码长度）为:

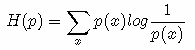
如果使用非真实分布 q(x) 来表示来自真实分布 p(x) 的平均编码长度，则是：

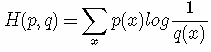
（因为用 q(x) 来编码的样本来自于分布 q(x) ，所以 H(p,q) 中的概率是 p(x)）。此时就将 H(p,q) 称之为交叉熵。举个例子。考虑一个随机变量 x，真实分布p(x)=(1/2,1/4,1/8,1/8)，非真实分布 q(x)=(1/4,1/4,1/4,1/4)，则H(p)=1.75 bits（最短平均码长），交叉熵:

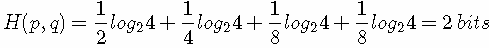
由此可以看出根据非真实分布 q(x) 得到的平均码长大于根据真实分布 p(x) 得到的平均码长。

我们再化简一下相对熵的公式。

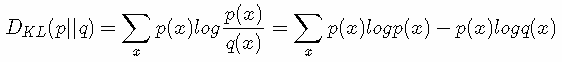
有没有发现什么？

熵的公式：

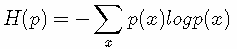
交叉熵的公式：

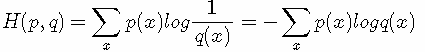
所以有：DKL(p||q)=H(p,q)−H(p)（当用非真实分布 q(x) 得到的平均码长比真实分布 p(x) 得到的平均码长多出的比特数就是相对熵）

又因为 DKL(p||q)≥0所以 H(p,q)≥H(p)（当 p(x)=q(x) 时取等号，此时交叉熵等于信息熵）并且当 H(p) 为常量时（注：在机器学习中，训练数据分布是固定的）最小化相对熵 DKL(p||q) 等价于最小化交叉熵 H(p,q) 也等价于最大化似然估计（具体参考Deep Learning 5.5）。在机器学习中，我们希望训练数据上模型学到的分布 P(model) 和真实数据的分布 P(real) 越接近越好，所以我们可以使其相对熵最小。但是我们没有真实数据的分布，所以只能希望模型学到的分布 P(model) 和训练数据的分布 P(train) 尽量相同。假设训练数据是从总体中独立同分布采样的，那么我们可以通过最小化训练数据的经验误差来降低模型的泛化误差。即：

希望学到的模型的分布和真实分布一致，P(model)≃P(real)
但是真实分布不可知，假设训练数据是从真实数据中独立同分布采样的P(train)≃P(real)
因此，我们希望学到的模型分布至少和训练数据的分布一致，P(train)≃P(model)

根据之前的描述，最小化训练数据上的分布 P(train)与最小化模型分布 P(model) 的差异等价于最小化相对熵，即 DKL(P(train)||P(model))。此时， P(train)就是DKL(p||q) 中的 p，即真实分布，P(model)就是 q。又因训练数据的分布 p 是给定的，所以求 DKL(p||q) 等价求 H(p,q)。得证，交叉熵可以用来计算学习模型分布与训练分布之间的差异。交叉熵广泛用于逻辑回归的Sigmoid和Softmax函数中作为损失函数使用。这篇文章先不说了。

5 总结

信息熵是衡量随机变量分布的混乱程度，是随机分布各事件发生的信息量的期望值，随机变量的取值个数越多，状态数也就越多，信息熵就越大，混乱程度就越大。当随机分布为均匀分布时，熵最大；信息熵推广到多维领域，则可得到联合信息熵；条件熵表示的是在 X 给定条件下，Y 的条件概率分布的熵对 X的期望。
相对熵可以用来衡量两个概率分布之间的差异。
交叉熵可以来衡量在给定的真实分布下，使用非真实分布所指定的策略消除系统的不确定性所需要付出的努力的大小。

或者：

信息熵是传输一个随机变量状态值所需的比特位下界（最短平均编码长度）。
相对熵是指用 q 来表示分布 p 额外需要的编码长度。
交叉熵是指用分布 q 来表示本来表示分布 p 的平均编码长度。

参考：

1) 吴军《数学之美》

2) 李航《统计学习方法》

3) 马春鹏《模式识别与机器学习》

4) https://www.zhihu.com/question/41252833 如何通俗的解释交叉熵与相对熵

5) https://www.zhihu.com/question/65288314/answer/244557337为什么交叉熵（cross-entropy）可以用于计算代价？

6) https://baike.baidu.com/item/%E4%BA%A4%E5%8F%89%E7%86%B5/8983241?fr=aladdin 交叉熵的百度百科解释

7) https://blog.csdn.net/saltriver/article/details/53056816信息熵到底是什么

－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－

3. 转自：https://blog.csdn.net/tsyccnh/article/details/79163834

关于交叉熵在loss函数中使用的理解
交叉熵（cross entropy）是深度学习中常用的一个概念，一般用来求目标与预测值之间的差距。以前做一些分类问题的时候，没有过多的注意，直接调用现成的库，用起来也比较方便。最近开始研究起对抗生成网络（GANs），用到了交叉熵，发现自己对交叉熵的理解有些模糊，不够深入。遂花了几天的时间从头梳理了一下相关知识点，才算透彻的理解了，特地记录下来，以便日后查阅。

信息论
交叉熵是信息论中的一个概念，要想了解交叉熵的本质，需要先从最基本的概念讲起。

1 信息量
首先是信息量。假设我们听到了两件事，分别如下：
事件A：巴西队进入了2018世界杯决赛圈。
事件B：中国队进入了2018世界杯决赛圈。
仅凭直觉来说，显而易见事件B的信息量比事件A的信息量要大。究其原因，是因为事件A发生的概率很大，事件B发生的概率很小。所以当越不可能的事件发生了，我们获取到的信息量就越大。越可能发生的事件发生了，我们获取到的信息量就越小。那么信息量应该和事件发生的概率有关。

假设XX是一个离散型随机变量，其取值集合为χχ,概率分布函数p(x)=Pr(X=x),x∈χp(x)=Pr(X=x),x∈χ,则定义事件X=x0X=x0的信息量为：

I(x0)=−log(p(x0))
I(x0)=−log(p(x0))

由于是概率所以p(x0)p(x0)的取值范围是[0,1][0,1],绘制为图形如下：

可见该函数符合我们对信息量的直觉
2 熵
考虑另一个问题，对于某个事件，有nn种可能性，每一种可能性都有一个概率p(xi)p(xi)
这样就可以计算出某一种可能性的信息量。举一个例子，假设你拿出了你的电脑，按下开关，会有三种可能性，下表列出了每一种可能的概率及其对应的信息量

序号事件概率p 信息量I
A 电脑正常开机 0.7 -log(p(A))=0.36
B 电脑无法开机 0.2 -log(p(B))=1.61
C 电脑爆炸了 0.1 -log(p(C))=2.30
注：文中的对数均为自然对数

我们现在有了信息量的定义，而熵用来表示所有信息量的期望，即：
H(X)=−∑i=1np(xi)log(p(xi))
H(X)=−∑i=1np(xi)log(p(xi))
其中n代表所有的n种可能性，所以上面的问题结果就是
H(X)===−[p(A)log(p(A))+p(B)log(p(B))+p(C))log(p(C))]0.7×0.36+0.2×1.61+0.1×2.300.804
H(X)=−[p(A)log(p(A))+p(B)log(p(B))+p(C))log(p(C))]=0.7×0.36+0.2×1.61+0.1×2.30=0.804
然而有一类比较特殊的问题，比如投掷硬币只有两种可能，字朝上或花朝上。买彩票只有两种可能，中奖或不中奖。我们称之为0-1分布问题（二项分布的特例），对于这类问题，熵的计算方法可以简化为如下算式：
H(X)==−∑i=1np(xi)log(p(xi))−p(x)log(p(x))−(1−p(x))log(1−p(x))
H(X)=−∑i=1np(xi)log(p(xi))=−p(x)log(p(x))−(1−p(x))log(1−p(x))
3 相对熵（KL散度）
相对熵又称KL散度,如果我们对于同一个随机变量 x 有两个单独的概率分布 P(x) 和 Q(x)，我们可以使用 KL 散度（Kullback-Leibler (KL) divergence）来衡量这两个分布的差异

维基百科对相对熵的定义

In the context of machine learning, DKL(P‖Q) is often called the information gain achieved if P is used instead of Q.

即如果用P来描述目标问题，而不是用Q来描述目标问题，得到的信息增量。

在机器学习中，P往往用来表示样本的真实分布，比如[1,0,0]表示当前样本属于第一类。Q用来表示模型所预测的分布，比如[0.7,0.2,0.1]
直观的理解就是如果用P来描述样本，那么就非常完美。而用Q来描述样本，虽然可以大致描述，但是不是那么的完美，信息量不足，需要额外的一些“信息增量”才能达到和P一样完美的描述。如果我们的Q通过反复训练，也能完美的描述样本，那么就不再需要额外的“信息增量”，Q等价于P。

KL散度的计算公式：
DKL(p||q)=∑i=1np(xi)log(p(xi)q(xi))(3.1)
(3.1)DKL(p||q)=∑i=1np(xi)log(p(xi)q(xi))

n为事件的所有可能性。
DKLDKL的值越小，表示q分布和p分布越接近
4 交叉熵
对式3.1变形可以得到：
DKL(p||q)==∑i=1np(xi)log(p(xi))−∑i=1np(xi)log(q(xi))−H(p(x))+[−∑i=1np(xi)log(q(xi))]
DKL(p||q)=∑i=1np(xi)log(p(xi))−∑i=1np(xi)log(q(xi))=−H(p(x))+[−∑i=1np(xi)log(q(xi))]
等式的前一部分恰巧就是p的熵，等式的后一部分，就是交叉熵：
H(p,q)=−∑i=1np(xi)log(q(xi))
H(p,q)=−∑i=1np(xi)log(q(xi))
在机器学习中，我们需要评估label和predicts之间的差距，使用KL散度刚刚好，即DKL(y||ŷ )DKL(y||y^)，由于KL散度中的前一部分−H(y)−H(y)不变，故在优化过程中，只需要关注交叉熵就可以了。所以一般在机器学习中直接用用交叉熵做loss，评估模型。

机器学习中交叉熵的应用
1 为什么要用交叉熵做loss函数？
在线性回归问题中，常常使用MSE（Mean Squared Error）作为loss函数，比如：
loss=12m∑i=1m(yi−yi^)2
loss=12m∑i=1m(yi−yi^)2
这里的m表示m个样本的，loss为m个样本的loss均值。
MSE在线性回归问题中比较好用，那么在逻辑分类问题中还是如此么？

2 交叉熵在单分类问题中的使用
这里的单类别是指，每一张图像样本只能有一个类别，比如只能是狗或只能是猫。
交叉熵在单分类问题上基本是标配的方法
loss=−∑i=1nyilog(yi^)(2.1)
(2.1)loss=−∑i=1nyilog(yi^)
上式为一张样本的loss计算方法。式2.1中n代表着n种类别。
举例说明,比如有如下样本

对应的标签和预测值

* 猫青蛙老鼠
Label 0 1 0
Pred 0.3 0.6 0.1
那么
loss==−(0×log(0.3)+1×log(0.6)+0×log(0.1)−log(0.6)
loss=−(0×log(0.3)+1×log(0.6)+0×log(0.1)=−log(0.6)
对应一个batch的loss就是
loss=−1m∑j=1m∑i=1nyjilog(yji^)
loss=−1m∑j=1m∑i=1nyjilog(yji^)
m为当前batch的样本数

3 交叉熵在多分类问题中的使用
这里的多类别是指，每一张图像样本可以有多个类别，比如同时包含一只猫和一只狗
和单分类问题的标签不同，多分类的标签是n-hot。
比如下面这张样本图，即有青蛙，又有老鼠，所以是一个多分类问题

对应的标签和预测值

* 猫青蛙老鼠
Label 0 1 1
Pred 0.1 0.7 0.8
值得注意的是，这里的Pred不再是通过softmax计算的了，这里采用的是sigmoid。将每一个节点的输出归一化到[0,1]之间。所有Pred值的和也不再为1。换句话说，就是每一个Label都是独立分布的，相互之间没有影响。所以交叉熵在这里是单独对每一个节点进行计算，每一个节点只有两种可能值，所以是一个二项分布。前面说过对于二项分布这种特殊的分布，熵的计算可以进行简化。

同样的，交叉熵的计算也可以简化，即
loss=−ylog(ŷ )−(1−y)log(1−ŷ )
loss=−ylog(y^)−(1−y)log(1−y^)
注意，上式只是针对一个节点的计算公式。这一点一定要和单分类loss区分开来。
例子中可以计算为：
loss猫loss蛙loss鼠===−0×log(0.1)−(1−0)log(1−0.1)=−log(0.9)−1×log(0.7)−(1−1)log(1−0.7)=−log(0.7)−1×log(0.8)−(1−1)log(1−0.8)=−log(0.8)
loss猫=−0×log(0.1)−(1−0)log(1−0.1)=−log(0.9)loss蛙=−1×log(0.7)−(1−1)log(1−0.7)=−log(0.7)loss鼠=−1×log(0.8)−(1−1)log(1−0.8)=−log(0.8)
单张样本的loss即为loss=loss猫+loss蛙+loss鼠loss=loss猫+loss蛙+loss鼠
每一个batch的loss就是：
loss=∑j=1m∑i=1n−yjilog(yji^)−(1−yji)log(1−yji^)
loss=∑j=1m∑i=1n−yjilog(yji^)−(1−yji)log(1−yji^)
式中m为当前batch中的样本量，n为类别数。

总结
路漫漫，要学的东西还有很多啊。

参考：

https://www.zhihu.com/question/65288314/answer/244557337
https://en.wikipedia.org/wiki/Kullback%E2%80%93Leibler_divergence
https://jamesmccaffrey.wordpress.com/2013/11/05/why-you-should-use-cross-entropy-error-instead-of-classification-error-or-mean-squared-error-for-neural-network-classifier-training/
－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－

4. 最大熵模型

from https://www.cnblogs.com/pinard/p/6093948.html

最大熵模型(maximum entropy model， MaxEnt)也是很典型的分类算法了，它和逻辑回归类似，都是属于对数线性分类模型。在损失函数优化的过程中，使用了和支持向量机类似的凸优化技术。而对熵的使用，让我们想起了决策树算法中的ID3和C4.5算法。理解了最大熵模型，对逻辑回归，支持向量机以及决策树算法都会加深理解。本文就对最大熵模型的原理做一个小结。

1. 熵和条件熵的回顾

　　　　在决策树算法原理(上)一文中，我们已经讲到了熵和条件熵的概念，这里我们对它们做一个简单的回顾。

　　　　熵度量了事物的不确定性，越不确定的事物，它的熵就越大。具体的，随机变量X的熵的表达式如下：

H (X) = - \sum i = 1 n p i l o g p i

　　　　其中n代表X的n种不同的离散取值。而 $p_{i}$

　　　　熟悉了一个变量X的熵，很容易推广到多个个变量的联合熵，这里给出两个变量X和Y的联合熵表达式：

H (X, Y) = - \sum i = 1 n p (x i, y i) l o g p (x i, y i)

　　　　有了联合熵，又可以得到条件熵的表达式H(Y|X)，条件熵类似于条件概率,它度量了我们的Y在知道X以后剩下的不确定性。表达式如下：

H (Y | X) = - \sum i = 1 n p (x i, y i) l o g p (y i | x i) =

　　　　用下面这个图很容易明白他们的关系。左边的椭圆代表H(X),右边的椭圆代表H(Y),中间重合的部分就是我们的互信息或者信息增益I(X,Y), 左边的椭圆去掉重合部分就是H(X|Y),右边的椭圆去掉重合部分就是H(Y|X)。两个椭圆的并就是H(X,Y)。

2. 最大熵模型的定义

　　　　最大熵模型假设分类模型是一个条件概率分布 $P (Y | X)$

　　　　给定一个训练集 $(x^{(1)}, y^{(1)}), (x^{(2)}, y^{(2)}), . . . ， (x^{(m)}, y^{(m)})$

　　　　在给定训练集的情况下，我们可以得到总体联合分布 $P (X, Y)$

　　　　用特征函数 $f (x, y)$

f (x, y) = {1 0 x 与 y 满 足 某 个 关 系

　　　　可以认为只要出现在训练集中出现的 $(x^{(i)}, y^{(i)})$

　　　　特征函数 $f (x, y)$

E P ⎯⎯⎯⎯ (f) = \sum x, y P ⎯⎯⎯⎯ (x, y) f (x, y)

　　　　特征函数 $f (x, y)$

E P (f) = \sum x, y P ⎯⎯⎯⎯ (x) P (y | x) f (x, y)

　　　　如果模型可以从训练集中学习，我们就可以假设这两个期望相等。即：

E P ⎯⎯⎯⎯ (f) = E P (f)

　　　　上式就是最大熵模型学习的约束条件，假如我们有M个特征函数 $f_{i} (x, y) (i = 1, 2..., M)$

　　　　这样我们就得到了最大熵模型的定义如下：

　　　　假设满足所有约束条件的模型集合为：

E P ⎯⎯⎯⎯ (f i) = E P (f i) (i = 1, 2, . . . M)

　　　　定义在条件概率分布 $P (Y | X)$

H (P) = - \sum x, y P ⎯⎯⎯⎯ (x) P (y | x) l o g P (y | x)

　　　　我们的目标是得到使 $H (P)$

3 . 最大熵模型损失函数的优化

　　　　在上一节我们已经得到了最大熵模型的函数 $H (P)$

m i n ⏟ P - H (P) = \sum x, y P ⎯⎯⎯⎯ (x) P (y | x) l o g P (y

　　　　约束条件为：

E P ⎯⎯⎯⎯ (f i) - E P (f i) = 0 (i = 1, 2, . . . M)

\sum y P (y | x) = 1

　　　　由于它是一个凸函数，同时对应的约束条件为仿射函数，根据凸优化理论，这个优化问题可以用拉格朗日函数将其转化为无约束优化函数，此时损失函数对应的拉格朗日函数 $L (P, w)$

L (P, w) \equiv - H (P) + w 0 (1 - \sum y P (y | x)) + \sum i = 1 M w i (

　　　　其中 $w_{i} (i = 1, 2, . . . m)$

　　　　我们的拉格朗日函数，即为凸优化的原始问题： $\underset{P}{\underset{⏟}{m i n}} \underset{w}{\underset{⏟}{m a x}} L (P, w)$

　　　　其对应的拉格朗日对偶问题为： $\underset{w}{\underset{⏟}{m a x}} \underset{P}{\underset{⏟}{m i n}} L (P, w)$

　　　　由于原始问题满足凸优化理论中的KKT条件，因此原始问题的解和对偶问题的解是一致的。这样我们的损失函数的优化变成了拉格朗日对偶问题的优化。

　　　　求解对偶问题的第一步就是求 $\underset{P}{\underset{⏟}{m i n}} L (P, w)$

ψ (w) = m i n ⏟ P L (P, w) = L (P w, w)

　　　　 $ψ (w)$

P w = a r g m i n ⏟ P L (P, w) = P w (y | x)

　　　　具体的是求 $L (P, w)$

\partial L ( P , w ) \partial P ( y | x ) = \sum x , y P ⎯⎯⎯⎯ ( x ) ( l o g P ( y | x ) +

= \sum x, y P ⎯⎯⎯⎯ (x) (l o g P (y | x) + 1 - w 0 - \sum i = 1 M w i

　　　　令偏导数为0，可以解出 $P (y | x)$

P (y | x) = e x p (\sum i = 1 M w i f i (x, y) + w 0 - 1) = e x

　　　　由于 $\sum_{y} P (y | x) = 1$

P w (y | x) = 1 Z w ( x ) e x p ( \sum i = 1 M w i f i ( x , y ) )

　　　　其中， $Z_{w} (x)$

Z w (x) = \sum y e x p (\sum i = 1 M w i f i (x, y))

　　　　这样我们就得出了 $P (y | x)$

　　　　对 $ψ (w)$

　　　　IIS也是启发式方法，它假设当前的参数向量是 $w$

　　　　IIS使用的方法是找到 $ψ (w + δ) - ψ (w)$

　　　　由于IIS一般只用于最大熵模型，适用范围不广泛，这里就不详述算法过程了，感兴趣的朋友可以直接参考IIS的论文The improved iterative scaling algorithm: A gentle introduction。

4. 最大熵模型小结

　　　　最大熵模型在分类方法里算是比较优的模型，但是由于它的约束函数的数目一般来说会随着样本量的增大而增大，导致样本量很大的时候，对偶函数优化求解的迭代过程非常慢，scikit-learn甚至都没有最大熵模型对应的类库。但是理解它仍然很有意义，尤其是它和很多分类方法都有千丝万缕的联系。　

　　　　惯例，我们总结下最大熵模型作为分类方法的优缺点：

　　　　最大熵模型的优点有：

　　　　a) 最大熵统计模型获得的是所有满足约束条件的模型中信息熵极大的模型,作为经典的分类模型时准确率较高。

　　　　b) 可以灵活地设置约束条件，通过约束条件的多少可以调节模型对未知数据的适应度和对已知数据的拟合程度

　　　　最大熵模型的缺点有：

　　　　a) 由于约束函数数量和样本数目有关系，导致迭代过程计算量巨大，实际应用比较难。

posted @ 2019-04-18 00:01 凌波微步_Arborday 阅读(2854) 评论(0) 编辑收藏举报

刷新页面返回顶部

凌波微步_Arborday