ABC 265
E - Warp(计数、枚举、DP)
Problem
在一个二维平面上,你从原点开始,可以移动\(N\)次,每次可以进行下面三种移动,假设当前位置是\((x,y)\)
- \((x,y)\rightarrow (x+A,y+B)\)
- \((x,y)\rightarrow (x+C,y+D)\)
- \((x,y)\rightarrow (x+E,y+F)\)
不过平面上还有\(M\)个障碍,不能移动到障碍上面。求进行\(N\)次移动移动之后,可以形成多少种不同的路径,答案对\(998244353\)取模
\(1\le N\le 300\),\(1\le M\le 10^5\),\(-10^9\le A,B,C,D,E,F\le 10^9\)
Solve
hit1:\(n\)很小hit2:类比从一个点只走右、上到另一个点的方案数的求法
定义\(dp[i][j][k]\)表示当前进行了\(i\)次操作\(1\),\(j\)次操作\(2\),\(k\)次操作\(3\)可以得到的路径条数。不过由于一个点可能通过相同的\(i,j,k\)得到,但由于执行顺序不同会导致路径不同,所以采用刷表法来转移\(dp\)
Code
#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int mod=998244353;
int dx[4],dy[4];
ll dp[305][305][305];
int main(){
ios::sync_with_stdio(false);
cin.tie(nullptr);
int n,m;
cin>>n>>m;
cin>>dx[0]>>dy[0]>>dx[1]>>dy[1]>>dx[2]>>dy[2];
map<pair<ll,ll>,bool>ob;
for(int i=0;i<m;i++){
int x,y;
cin>>x>>y;
ob[{x,y}]=1;
}
dp[0][0][0]=1;
ll ans=0;
for(int i=0;i<=n;i++)
for(int j=0;j<=n;j++)
for(int k=0;k<=n;k++){
if(i+j+k>n) break;
ll xx=i*dx[0]+j*dx[1]+k*dx[2];
ll yy=i*dy[0]+j*dy[1]+k*dy[2];
if(ob.find({xx,yy})!=ob.end()) continue;
if(i+j+k==n) ans=(ans+dp[i][j][k])%mod;
else{
dp[i+1][j][k]=(dp[i+1][j][k]+dp[i][j][k])%mod;
dp[i][j+1][k]=(dp[i][j+1][k]+dp[i][j][k])%mod;
dp[i][j][k+1]=(dp[i][j][k+1]+dp[i][j][k])%mod;
}
}
cout<<ans<<'\n';
}
F.Manhattan Cafe(DP优化)
Problem
定义两个长度为\(N\)的序列\(X、Y\)之间的距离为\(\text{dis}(X,Y)=\sum_{i+0}^N|X_i-Y_i|\)。现在给定两个长度为\(N\)的序列\(p,q\)和一个整数\(D\),问有多少个长度为\(N\)的序列\(r\)满足\(\text{dis}(q,r)\le D\)并且\(\text{}(p,r)\le D\)
\(1\le N\le 100\),\(1\le D\le 1000\),\(-1000\le p_i,q_i\le 1000\)
Solve
定义\(dp[t][i][j]\)表示\(\sum_{k=1}^t|p_k-r_k|=i\)并且\(\sum_{k=1}^t|q_k-r_k|=j\)的方案数。那么转移就可以写成这样
f1[1001][1001],f2[1001][1001];
f1[0][0]=1;
for(int k=1;k<=n;k++){
memset(f2,0,sizeof f2);
int x=p[k],y=q[k];
for(int rt=-2000;rt<=2000;rt++){ //枚举rt
int di=abs(x-rt);
int dj=abs(y-rt);
if(min(di,dj)>D) continue;
for(int i=0;i<=D-di;i++) //枚举dp[t-1][i][j]的i,j
for(int j=0;j<=D-dj;j++)
f2[i+di][j+dj]+=f1[i][j];
}
f1=f2;
}
但问题是这样的时间复杂度是\(O(ND^3)\),明显会超时。考虑优化,如果记\(s=|p_t-q_t|\),那么所有\((d_i,d_j)\)的组合可以分成\(3\)类
- \((s,0),(s-1,1),\cdots,(0,s)\)
- \((s+1,1),(s+2,2),(s+3,3),\cdots\)
- \((1,s+1),(2,s+2),(3,s+3),\cdots\)
对于每种情况单独用\(O(D^2)\)转移,这样总的时间复杂度就是\(O(ND^2)\)。
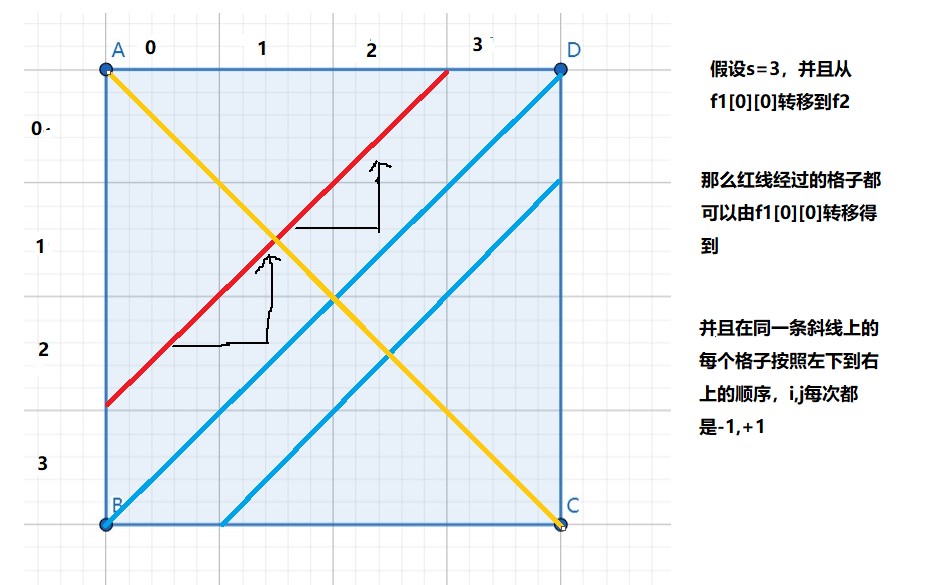
其中左下到右上的线对应情况\(1\)的转移,左上到右下对应情况\(2,3\)的转移
\(dp_2[i][j]=\sum_{k=0}^{\min(i,j)}f_1[i-k][j+k]\)
\(f_2[i][j]+=dp_2[i][j-s]=\sum_{k=0}^{\min(i,j-s)}f_1[i-k][j-s+k]\)
\(dp_3[i][j]=\sum_{k=0}^{min(i,j)}f_1[i-k][j-k]\)
\(f_2[i+1][j+s+1]+=dp_3[i][j]=\sum_{k=0}^{min(i,j)}f_1[i-k][j-k]\)
Code
#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int mod=998244353;
int main(){
ios::sync_with_stdio(false);
cin.tie(nullptr);
int n,d;
cin>>n>>d;
vector<int>q(n),p(n);
for(auto &x:p) cin>>x;
for(auto &x:q) cin>>x;
vector<vector<ll>>dp(d+1,vector<ll>(d+1));
dp[0][0]=1;
for(int k=0;k<n;k++){
int s=abs(p[k]-q[k]);
vector<vector<ll>>dp2(d+1,vector<ll>(d+1)),dp3(d+1,vector<ll>(d+1)),nxt(d+1,vector<ll>(d+1));
for(int i=0;i<=d;i++)
for(int j=0;j<=d;j++){
dp2[i][j]=dp[i][j];
if(i!=0&&j!=d) dp2[i][j]=(dp2[i][j]+dp2[i-1][j+1])%mod;
}
for(int i=0;i<=d;i++)
for(int j=0;j<=d;j++){
int si=i,sj=j-s;
if(sj<0) si+=sj,sj=0;
if(si>=0&& si<=d && sj>=0){
nxt[i][j]=(nxt[i][j]+dp2[si][sj])%mod;
}
int ti=i-(s+1),tj=j+1;
if(ti>=0&&tj<=d){
nxt[i][j]=(nxt[i][j]-dp2[ti][tj]+mod)%mod;
}
}
for(int i=0;i<=d;i++)
for(int j=0;j<=d;j++){
dp3[i][j]=dp[i][j];
if(i!=0&&j!=0){
dp3[i][j]=(dp3[i][j]+dp3[i-1][j-1])%mod;
}
if(i+1<=d&&j+s+1<=d){
nxt[i+1][j+s+1]=(nxt[i+1][j+s+1]+dp3[i][j])%mod;
}
if(i+s+1<=d&&j+1<=d){
nxt[i+s+1][j+1]=(nxt[i+s+1][j+1]+dp3[i][j])%mod;
}
}
dp=nxt;
}
ll ans=0;
for(int i=0;i<=d;i++)
for(int j=0;j<=d;j++)
ans=(ans+dp[i][j])%mod;
cout<<ans<<'\n';
}
G.012 Inversion(线段树)
Problem
给定一个长度为\(N\)并且只包含\(0、1、2\)的序列\(A\),进行\(Q\)次操作,每次操作有两种类型
1 L R:输出区间\([L,R]\)之间的逆序对数量2 L R S T U:对每一个\(L\le i \le R\),如果\(A_i\)是\(0\),就把\(A_i\)变成\(S\),如果是\(1\),就变成\(T\),如果是\(2\),就变成\(U\)。
\(1\le N,Q\le 10^5\),\(0\le A_i,S,T,U\le 2\)
Solve
线段树维护一下量
- 区间中\(0、1、2\)的数量
- 区间中\(10、20、21\)的数量(其实是逆序对组合的数量,容易发现只有三种组合)
由于有区间修改,所以要下传标记,考虑如何下传。
我们下传标记,其实就是记录原来区间内\(0、1、2\)分别变成了什么。一开始我们使用一个\(\text{lazy}[3]\)来表示,初始肯定是\(\text{lazy}[0]=0,\text{lazy}[1]=1,\text{lazy}[2]=2\)。现在考虑对一个区间进行两次修改,比如先把\(2\)变成\(1\),再把\(1\)变成\(0\),在第一次修改中,\(\text{lazy}[2]=1\),第二次修改,由于修改了\(1\),但原来的\(2\)都变成了\(1\),就变成了一个链式传递关系,此时\(\text{lazy}[2]=\text{op}[\text{lazy}[2]]\),其中\(\text{op}[i]\)表示这次操作的时候把\(i\)变成了\(\text{op}[i]\)。下放标记的时候,对于两个儿子来说,父亲的\(\text{lazy}\)数组就变成了\(\text{op}\)数组
Code
#include <bits/stdc++.h>
#define LL long long
#define ls rt<<1
#define rs rt<<1|1
using namespace std;
const int N=1e5+10;
struct node{
LL num1[3];
LL num2[3][3];
int tag,lazy[3];
}tr[N*4];
int a[N];
int c[3],tt[3];
LL tmp[3][3];
void pushup(node &rt,node ll ,node rr){
for(int i=0;i<3;i++) rt.num1[i]=ll.num1[i]+rr.num1[i];
for(int i=0;i<3;i++)
for(int j=0;j<3;j++)
if(i!=j)
rt.num2[i][j]=ll.num2[i][j]+rr.num2[i][j]+ll.num1[i]*rr.num1[j];
}
void build(int rt,int l,int r){
for(int i=0;i<3;i++) tr[rt].lazy[i]=i;
if(l==r){
tr[rt].num1[a[l]]++;
return;
}
int mid=(l+r)>>1;
build(ls,l,mid);
build(rs,mid+1,r);
pushup(tr[rt],tr[ls],tr[rs]);
}
void update(int rt,int q[]){
for(int i=0;i<3;i++) tt[i]=0;
for(int i=0;i<3;i++)
for(int j=0;j<3;j++) tmp[i][j]=0;
for(int i=0;i<3;i++) tr[rt].lazy[i]=q[tr[rt].lazy[i]];
for(int i=0;i<3;i++) tt[q[i]]+=tr[rt].num1[i];
for(int i=0;i<3;i++) tr[rt].num1[i]=tt[i];
for(int i=0;i<3;i++)
for(int j=0;j<3;j++)
if(q[i]!=q[j]) tmp[q[i]][q[j]]+=tr[rt].num2[i][j];
for(int i=0;i<3;i++)
for(int j=0;j<3;j++)
tr[rt].num2[i][j]=tmp[i][j];
tr[rt].tag=1;
}
void pushdown(int rt){
if(tr[rt].tag){
update(ls,tr[rt].lazy);
update(rs,tr[rt].lazy);
tr[rt].tag=0;
for(int i=0;i<3;i++) tr[rt].lazy[i]=i;
}
}
void modify(int rt,int L,int R,int l,int r){
if(l<=L&&R<=r){
update(rt,c);
return;
}
pushdown(rt);
int mid=(L+R)>>1;
if(l<=mid) modify(ls,L,mid,l,r);
if(r>mid) modify(rs,mid+1,R,l,r);
pushup(tr[rt],tr[ls],tr[rs]);
}
node query(int rt,int L,int R,int l,int r){
if(l<=L&&R<=r){
return tr[rt];
}
pushdown(rt);
int mid=(L+R)>>1;
if(r<=mid) return query(ls,L,mid,l,r);
else if(l>mid) return query(rs,mid+1,R,l,r);
else{
node res;
node ll=query(ls,L,mid,l,mid),rr=query(rs,mid+1,R,mid+1,r);
pushup(res,ll,rr);
return res;
}
}
int main(){
ios::sync_with_stdio(false);
cin.tie(nullptr);
int n,q;
cin>>n>>q;
for(int i=1;i<=n;i++) cin>>a[i];
build(1,1,n);
for(int i=1;i<=q;i++){
int op;
cin>>op;
if(op==1){
int l,r;
cin>>l>>r;
node t=query(1,1,n,l,r);
LL res=0;
res=t.num2[1][0]+t.num2[2][0]+t.num2[2][1];
cout<<res<<'\n';
}else{
int l,r;
cin>>l>>r;
for(int i=0;i<3;i++) cin>>c[i];
modify(1,1,n,l,r);
}
}
}


