计算几何泛做1
结合二分
POJ 2318 TOYS
Problem
在二维平面上给定一个矩阵,矩形里面有若干不相交的直线把矩阵分为若干个区域,保证直线会穿过矩形的上下边,现在给出若干个点,问每个区域包含几个点。给出的直线按照从左往右的顺序
Solve
对于一个点,利用叉积去二分判断它在哪条边右边
Code
#include <iostream>
#include <algorithm>
#include <cmath>
#include <vector>
using namespace std;
struct Point{
int x,y;
Point(){}
Point(int x,int y):x(x),y(y){}
int operator ^ (const Point &t)const{
return x*t.y-y*t.x;
}
Point operator - (const Point &t)const{
return Point(x-t.x,y-t.y);
}
};
struct Seg{
Point st,ed;
Seg(){}
Seg(Point st,Point ed):st(st),ed(ed){}
}L[5005];
int ans[5005];
int main(){
ios::sync_with_stdio(false);
cin.tie(0);
int n,m,x1,x2,y1,y2;
while(cin>>n,n)
{
cin>>m>>x1>>y1>>x2>>y2;
L[0]=Seg(Point(x1,y2),Point(x1,y1));
for(int i=1;i<=n;i++){
cin>>L[i].ed.x>>L[i].st.x;
L[i].ed.y=y1,L[i].st.y=y2;
}
L[n+1]=Seg(Point(x2,y2),Point(x2,y1));
for(int i=0;i<=n+1;i++) ans[i]=0;
for(int i=1;i<=m;i++){
int x,y;
cin>>x>>y;
Point p=Point(x,y);
int l=0,r=n+1;
while(l<=r){
int mid=l+r>>1;
if(((p-L[mid].st)^(L[mid].ed-L[mid].st))<=0) r=mid-1;
else l=mid+1;
}
ans[r]++;
}
for(int i=0;i<=n;i++)
cout<<i<<": "<<ans[i]<<'\n';
cout<<'\n';
}
}
极角排序
UVA 11696 Beacons
Problem
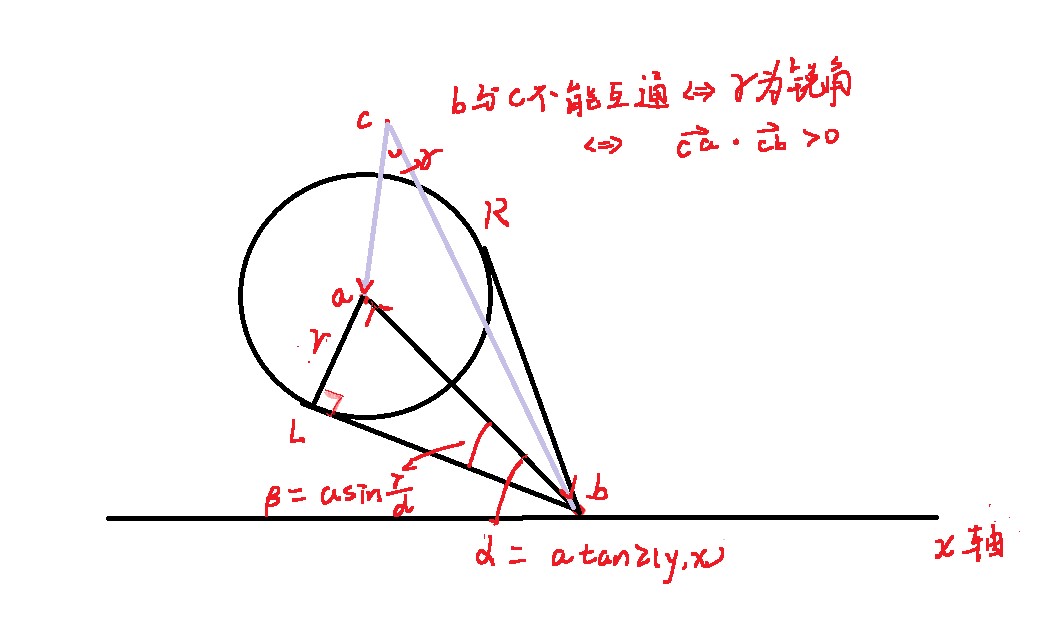
古代战争通过狼烟传递消息,平面上有\(n\)个狼烟点,\(m\)座山峰(半径为\(r\)的圆),两个狼烟点可以传递消息当且仅当它们之间的直线不经过任何一座山峰的区域。现在从可以点燃第一个狼烟,消息具有传递性,就是一个狼烟升起后,在它周围与它可以传递信息的狼烟点都会升起狼烟。但可能存在狼烟点没办法通过这样的消息传递来升起狼烟,从而需要骑士传递信息到该狼烟点,问最少需要多少骑士
Solve
标记每对可以互相到达的点,会形成一个无向图,最后看这个无向图里面有几个连通块即可
Code
#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int N=1005;
const double eps=1e-8;
int n,m;
struct Point{
int x,y;
void input(){
cin>>x>>y;
}
bool operator < (const Point &t )const{
return y==t.y?x<t.x:y<t.y;
}
Point operator + (const Point &t)const{
return {x+t.x,y+t.y};
}
Point operator - (const Point &t)const{
return {x-t.x,y-t.y};
}
int operator * (const Point &t)const{
return x*t.x+y*t.y;
}
int operator ^ (const Point &t) const{
return x*t.y-y*t.x;
}
}p[N],c[N];;
int r[N];
int vis[N];
int g[N][N];
double get_dist(Point a,Point b){
return sqrt(1.0*(a.x-b.x)*(a.x-b.x)+1.0*(a.y-b.y)*(a.y-b.y));
}
vector<int>E[N*N];
void build(){
sort(p+1,p+1+n);
for(int i=1;i<=n;i++){
vector<pair<double,int>>v;
for(int j=i+1;j<=n;j++){
v.emplace_back(atan2(p[j].y-p[i].y,p[j].x-p[i].x),j);
}
sort(v.begin(), v.end());
for(int j=1;j<=m;j++){
double alpha=atan2(c[j].y-p[i].y,c[j].x-p[i].x);
double theta=asin(1.0*r[j]/get_dist(c[j],p[i]));
double L=alpha-theta,R=alpha+theta;
int id=lower_bound(v.begin(), v.end(),make_pair(L,-1))-v.begin();
for(int k=id;k<v.size()&&v[k].first<=R;k++){
if((p[i]-p[v[k].second])*(c[j]-p[v[k].second])>0) //如果是锐角,说明不可以相互传递消息
g[i][v[k].second]=g[v[k].second][i]=1;
}
}
}
}
void dfs(int u){
vis[u]=1;
for(int i=1;i<=n;i++){
if(!vis[i]&&!g[u][i]) dfs(i);
}
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(nullptr);
int T;
cin>>T;
while(T--){
cin>>n>>m;
memset(g,0,sizeof g);
for(int i=1;i<=n;i++) p[i].input();
for(int i=1;i<=m;i++) c[i].input(),cin>>r[i];
build();
int res=0;
memset(vis,0,sizeof vis);
for(int i=1;i<=n;i++){
if(!vis[i]) dfs(i),res++;
}
cout<<res-1<<'\n';
}
}
POJ 2280 Amphiphilic Carbon Molecules
Problem
平面上有若干个黑白点,现在要求你找一个直线,使得直线一侧的白点数加上另一侧的黑点数最大
Solve
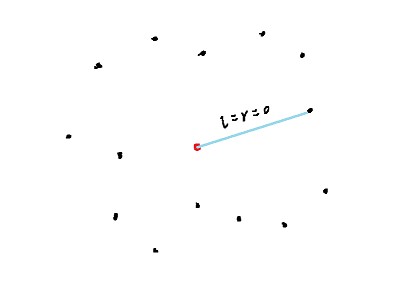
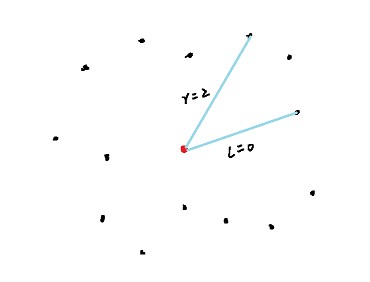
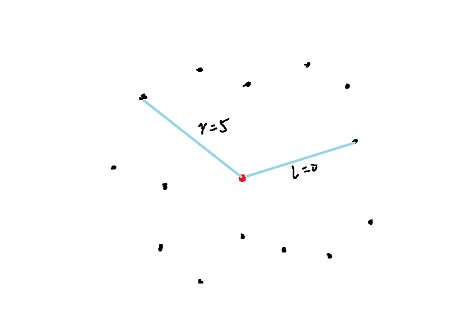
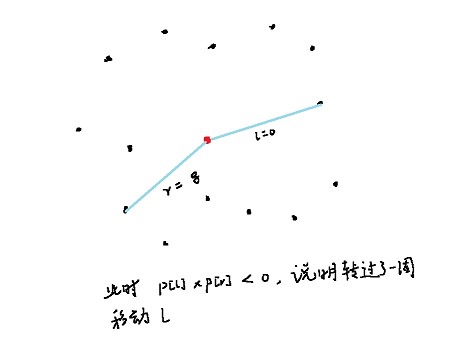
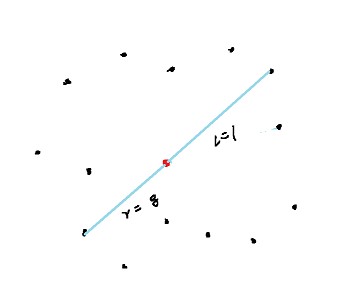
枚举每一个点,以这个点为基点,对其他点做极角排序,然后用双指针统计答案。
这里可以把黑点做关于基点的对称点,这样统计的时候只需要统计一边的点的数量的了。
时间复杂度\(O(n^2logn)\)
Code
#include <iostream>
#include <algorithm>
#include <cmath>
using namespace std;
const int N=1005;
struct Point{
int x,y,t;
double rad;
bool operator < (const Point &t){
return rad<t.rad;
}
int operator ^ (const Point t){
return x*t.y-y*t.x;
}
};
Point p[N],pp[N];
int main()
{
int n;
while(cin>>n,n){
int res=0;
for(int i=1;i<=n;i++) cin>>p[i].x>>p[i].y>>p[i].t;
for(int i=1;i<=n;i++){
int m=0;
for(int j=1;j<=n;j++){
if(i==j) continue;
pp[m].x=p[j].x-p[i].x;
pp[m].y=p[j].y-p[i].y;
if(p[j].t==1){
pp[m].x=-pp[m].x;
pp[m].y=-pp[m].y;
}
pp[m].rad=atan2(1.0*pp[m].y,1.0*pp[m].x);
m++;
}
sort(pp,pp+m);
int sum=2,l=0,r=0;
while(l<m){
if(l==r) {
r=(r+1)%m;
sum++;
}
while(l!=r&&(pp[l]^pp[r])>=0){
r=(r+1)%m;
sum++;
}
l++;
sum--;
res=max(res,sum);
}
}
cout<<res<<'\n';
}
}


