SAM复习
定义
SAM的定义
字符串\(s\)的SAM是一个可接受\(s\)的所有后缀的最小\(DFA\)(确定的有穷自动机)，可以参考编译原理的龙书(强烈推荐)
- SAM是一张有向无环图。节点被称作状态，边被称作状态之间的转移
- 存在一个初始状态\(t_0\)，其他各结点都可以从\(t_0\)出发到达
- 没有输出\(\epsilon\)之上的转移，即没有边标号为\(\epsilon\)(空字符串)的转移
- 对每个状态\(s\)和每个输入符号\(a\)，有且仅有一条标号为\(a\)的边离开
- 存在一个或多个终止状态。从\(t_0\)出发转移到一个终止状态，则路径上的所有转移连接起来构成了\(s\)的一个后缀。从\(t_0\)出发到达的每一个结点上路径的转移是\(s\)的一个子串。
- 最小的意思是\(DFA\)中的状态数目最少，但又可以表示所有状态。(结点最少)
重要概念
结束为止endpos
- 定义：对于\(s\)的任意非空子串\(t\)，即\(endpos(t)\)为子串\(t\)在\(s\)中的所有结束位置
- 等价类：两个子串\(t_1\)和\(t_2\)的\(endpos\)集合可能相同，即\(endpos(t_1)=endpos(t_2)\)。这样所有字符串\(s\)的非空子串都可以根据他们的\(endpos\)集合划分成若干个等价类
- SAM中的每个状态对应一个或多个\(endpos\)相同的子串。SAM的状态个数=等价类个数+1，每个状态是一个等价类
- 引理1：字符串\(s\)的两个非空子串\(u\)和\(w\)\((|u|\le |w|)\)的\(endpos\)相同，当且仅当字符串\(u\)的每次出现，都是以\(w\)后缀的形式出现。比如\(s=abcdefgdefgpfg\)，令\(u=fg\)，\(w=defg\)，显然，\(endpos(u)\ne endpos(w)\)，因为\(s\)中出现了\(pfg\)，\(u\)出现了，但不是以\(w\)后缀的形式
- 引理2：考虑两个非空子串\(u\)和\(w\)(\(|u|\le |w|\))。要么\(endpos(u)\cap endpos(w) =\varnothing\)，要么\(endpos(w)\subseteq endpos(u)\)，取决于\(u\)是否为\(w\)的一个后缀（可以用上面的例子解释)
- 引理3：考虑一个\(endpos\)等价类，将类中的所有子串按长度非递增的顺序排序。那么每个子串都是它前一个子串的后缀，即较短的子串是较长子串的后缀。记这个等价类中最长串长度为\(maxlen\)，最短串长度为\(minlen\)，那么这个等价类中的子串长度恰好覆盖了整个区间\([minlen,maxlen]\)
后缀链接link
考虑SAM中某个不是\(t_0\)的状态\(v\)。状态\(v\)对应于一个等价类，如果定义\(w\)为这个等价类中最长串，那么这个等价类中的其他字符串都是\(w\)的后缀。
并且\(w\)的前几个后缀(按长度降序考虑)全部包含于这个等价类中，且其他后缀在其他等价类中。什么意思，还是用\(s=abcdefgdefgpfg\)这个例子，\(w=defg\)，假设\(w\)是它所在\(endpos\)的代表元，那么\(endpos(w)=\{defg,efg\}\)，但\(fg,g\)都是\(w\)的后缀，但它们与\(w\)不在同一个等价类中
记\(t\)为不与\(w\)在同一个等价类中但是\(w\)的后缀的最长中的一个，显然\(|t|=minlen-1\)。
于是在状态图中，我们从\(w\)所在的等价类\(v\)向\(t\)所在等价类连一条件记为\(link(v)\)，这样的边只有一条
- 引理4：所有后缀链接构成一棵根节点为\(t_0\)的树
- 引理5：通过\(endpos\)集合构造的树（每个子节点的\(subset\) 都包含在父节点的 \(subset\)中）与通过后缀链接\(link\)构造的树相同。
这样从某个等价类 \(E\) 不断跳 \(link\) 到初始结点 \(P\) 就可以访问 \(E\) 中最长子串 \(w\) 的每一个后缀
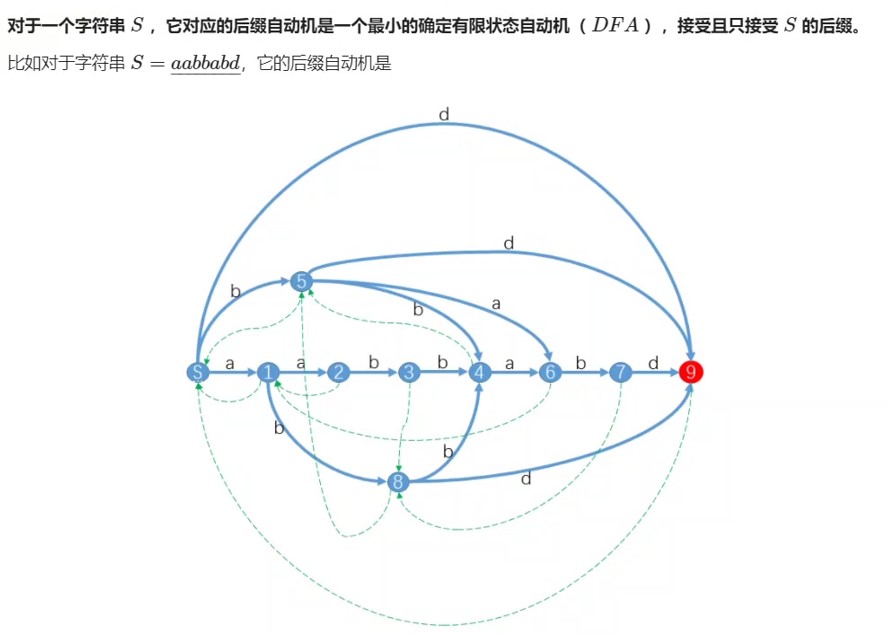
在图中可以看出，每个结点可以表示的字符串，他们的\(endpos\)是相同的，也就是说一个节点可以表示的字符串就是一个等价类。
其中蓝色的边是\(SAM\)中有向图的边，虚线的蓝色边为后缀连接\(link\)，构成了一棵树
复杂度
- 空间复杂度\(O(n|\Sigma|)\)，其中\(|\Sigma|\)为字符集的大小
- 时间复杂度\(O(n)\)
- SAM 的大小（状态数和转移数）为 线性的
构造方法
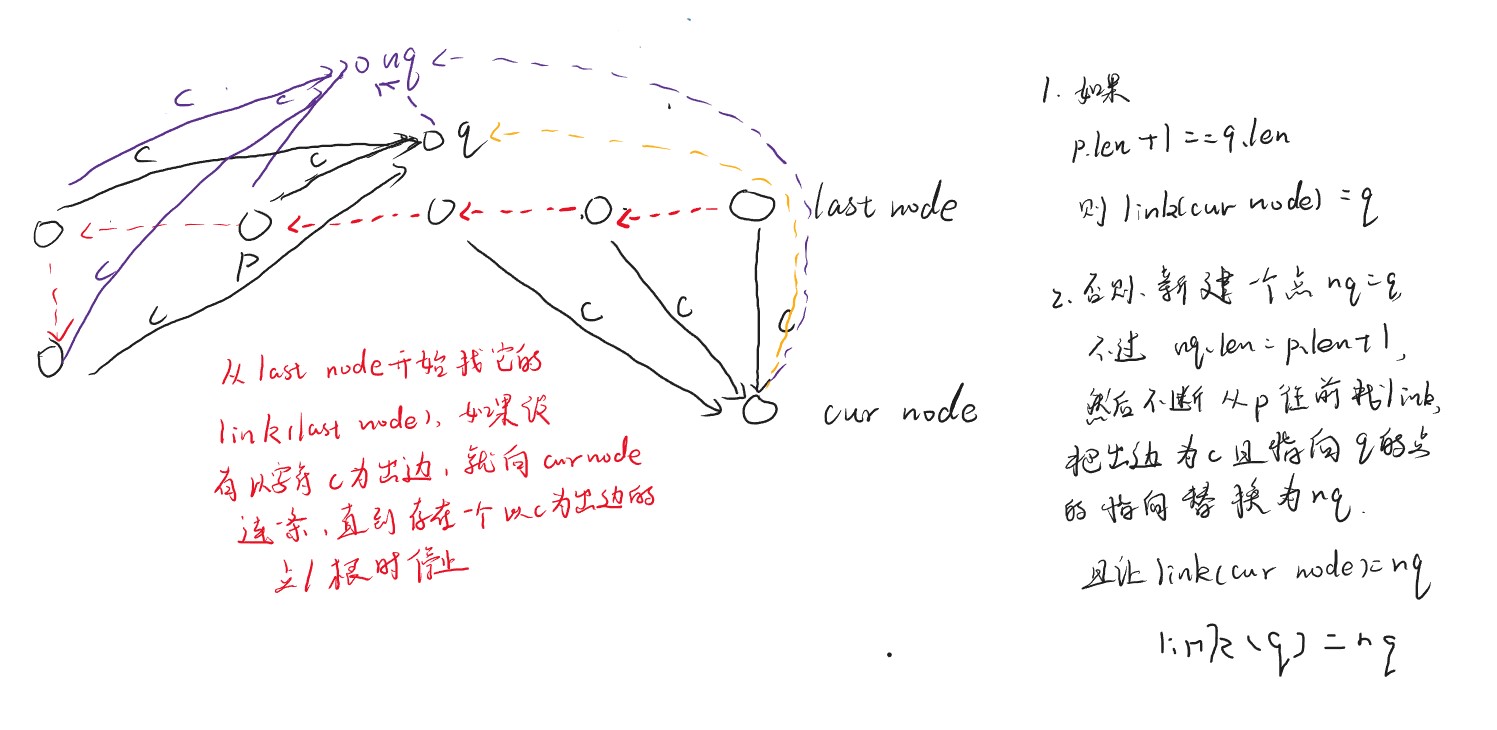
我们构建 \(SAM\) 的时候实际上是构建了串的每个前缀（按次序一位一位构造)
一般可以先求出\(SAM\)，然后把\(link\)构成的树重新构建一遍
模板
#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int N=2e6+10;
struct Node{
int len,link;
int ch[26];
}node[N];
int last=1,idx=1;
ll dp[N];
void SAM_Extend(int c){
int p=last,cur=++idx; //每次新加入的点是一个前缀
last=cur;
dp[idx]=1;
node[cur].len=node[p].len+1;
for(;p&&!node[p].ch[c];p=node[p].link) node[p].ch[c]=cur;
if(!p) node[cur].link=1;
else{
int q=node[p].ch[c];
if(node[q].len==node[p].len+1){
node[cur].link=q;
}else{
int nq=++idx;
node[nq]=node[q];
node[nq].len=node[p].len+1;
node[cur].link=node[q].link=nq;
for(;p&&node[p].ch[c]==q;p=node[p].link) node[p].ch[c]=nq;
}
}
}
//构建 link树
struct edges{
int v,nxt;
}e[N];
int cnt,head[N];
void add(int u,int v){
e[cnt]={v,head[u]},head[u]=cnt++;
}
//一顿操作
ll ans;
void dfs(int u){
for(int i=head[u];~i;i=e[i].nxt){
int v=e[i].v;
dfs(v);
dp[u]+=dp[v];
}
if(dp[u]>1) ans=max(ans,dp[u]*node[u].len);
}
int main(){
ios::sync_with_stdio(false);
cin.tie(nullptr);
memset(head,-1,sizeof head);
string s;
cin>>s;
int n=s.size();
for(int i=0;i<n;i++) SAM_Extend(s[i]-'a');
for(int i=2;i<=idx;i++) add(node[i].link,i);
dfs(1);
cout<<ans<<'\n';
return 0;
}
常用性质
- 在\(Link\)树中，每个节点代表的子串的出现次数等于其子树中叶子节点的个数，可以认为，所有叶子节点个数等于字符串总长度，每个叶子节点代表一个结束位置，则一个节点的的所有叶子代表的位置构成了这个节点的\(endpos\)位置集合，一个节点代表不止一个子串，它包含的子串个数=\(len[u]-len[fail[u]]\)
应用
- 检查字符串是否出现
- 不同子串个数
- 方法一：SAM生成的有向无环图中，每条路径对应一个子串(不一定从起点出发)，所以问题就是统计DAG上的路径条数，用DP计算即可。\(dp_u=1+\sum_{v\in son(u)}dp_v\)，最后答案就是\(dp_1-1\)，减去一个空串
- 方法二：在\(link\)树上求，每个节点对应的子串数量是\(len(i)-len(link(i))=maxlen(i)-maxlen(link(i))\)
- 所有不同子串的总长度
- 字典序第\(k\)大子串
- 最小循环移位
- 出现次数
- 假设模式串为\(P\)，文本串为\(T\)，那么构造出\(T\)的SAM后，在\(link\)树上找到\(P\)所在的节点，对应节点的\(endpos\)大小就是\(P\)的出现次数。\(endpos\)大小直接在\(link\)数上从子节点递推即可。
- 其实就是求\(link\)树上子树的大小，而根据构造方式，容易发现，叶子节点一定是一个前缀，所以在SAM的时候可以顺便记录一下前缀节点。形象的图，非常好理解
- 所有出现位置
- 最短的没有出现的字符串
- 两个字符串的最长公共子串
- 多个字符串间的最长公共子串
广义后缀自动机
常见的伪广义后缀自动机
- 通过用特殊符号
#将多个串直接连接后，再建立 SAM - 对每个串，重复在同一个 SAM 上进行建立，每次建立前，将 \(last\) 指针置零
构造方法
- 将所有字符串插入到字典树中
- 从字典树的根节点开始进行\(BFS\) ，记录下顺序以及每个节点的父亲节点
- 将得到的\(BFS\)序列按照顺序，对每个节点在原字典树上进行构建，注意不能将
len小于当前len的数据进行操作
性质
和后缀自动机类似
应用
- 所有字符中不同子串个数
- 多个字符串间的最长公共子串
- 给定多个字符串，求每个字符串本质不同的子串的个数
模板
#include <bits/stdc++.h>
using namespace std;
const int MAXN = 2000000; // 双倍字符串长度
const int CHAR_NUM = 30; // 字符集个数，注意修改下方的 (-'a')
struct exSAM {
int len[MAXN]; // 节点长度
int link[MAXN]; // 后缀链接，link
int next[MAXN][CHAR_NUM]; // 转移
int tot; // 节点总数：[0, tot)
void init() { // 初始化函数
tot = 1;
link[0] = -1;
}
int insertSAM(int last, int c) { // last 为父 c 为子
int cur = next[last][c];
if (len[cur]) return cur;
len[cur] = len[last] + 1;
int p = link[last];
while (p != -1) {
if (!next[p][c])
next[p][c] = cur;
else
break;
p = link[p];
}
if (p == -1) {
link[cur] = 0;
return cur;
}
int q = next[p][c];
if (len[p] + 1 == len[q]) {
link[cur] = q;
return cur;
}
int clone = tot++;
for (int i = 0; i < CHAR_NUM; ++i)
next[clone][i] = len[next[q][i]] != 0 ? next[q][i] : 0;
len[clone] = len[p] + 1;
while (p != -1 && next[p][c] == q) {
next[p][c] = clone;
p = link[p];
}
link[clone] = link[q];
link[cur] = clone;
link[q] = clone;
return cur;
}
int insertTrie(int cur, int c) {
if (next[cur][c]) return next[cur][c]; // 已有该节点 直接返回
return next[cur][c] = tot++; // 无该节点 建立节点
}
void insert(const string &s) {
int root = 0;
for (auto ch : s) root = insertTrie(root, ch - 'a');
}
void insert(const char *s, int n) {
int root = 0;
for (int i = 0; i < n; ++i)
root =
insertTrie(root, s[i] - 'a'); // 一边插入一边更改所插入新节点的父节点
}
void build() {
queue<pair<int, int>> q;
for (int i = 0; i < 26; ++i)
if (next[0][i]) q.push({i, 0});
while (!q.empty()) { // 广搜遍历
auto item = q.front();
q.pop();
auto last = insertSAM(item.second, item.first);
for (int i = 0; i < 26; ++i)
if (next[last][i]) q.push({i, last});
}
}
} exSam;
char s[1000100];
int main() {
int n;
cin >> n;
exSam.init();
for (int i = 0; i < n; ++i) {
cin >> s;
int len = strlen(s);
exSam.insert(s, len);
}
exSam.build();
long long ans = 0;
for (int i = 1; i < exSam.tot; ++i) {
ans += exSam.len[i] - exSam.len[exSam.link[i]];
}
cout << ans << endl;
}
更好写的模板
#include <bits/stdc++.h>
using namespace std;
const int N=2e6+10;
struct Node{
int len,link;
int ch[26];
}node[N];
int tot=1,last=1;
int insert(int c,int last){
int p=last;
if(node[p].ch[c]){
int q=node[p].ch[c];
if(node[q].len==node[p].len+1) return q;
else{
int nq=++tot;
node[nq]=node[q];
node[nq].len=node[p].len+1;
node[q].link=nq;
for(;p&&node[p].ch[c]==q;p=node[p].link) node[p].ch[c]=nq;
return nq;
}
}
int cur=++tot;
node[cur].len=node[p].len+1;
for(;p&&!node[p].ch[c];p=node[p].link) node[p].ch[c]=cur;
if(!p) node[cur].link=1;
else{
int q=node[p].ch[c];
if(node[q].len==node[p].len+1) node[cur].link=q;
else{
int nq=++tot;
node[nq]=node[q];
node[nq].len=node[p].len+1;
node[q].link=node[cur].link=nq;
for(;p&&node[p].ch[c]==q;p=node[p].link) node[p].ch[c]=nq;
}
}
return cur;
}
int main(){
ios::sync_with_stdio(false);
cin.tie(nullptr);
int n;
cin>>n;
for(int i=1;i<=n;i++){
string s;
cin>>s;
last=1;
for(int j=0;s[j];j++) {
last=insert(s[j]-'a',last);
}
}
long long ans=0;
for(int i=1;i<=tot;i++)
ans+=node[i].len-node[node[i].link].len;
cout<<ans<<'\n';
}
参考推荐博客
后缀自动机(SAM)奶妈式教程
